Yonggeun Shin

Yonggeun Shin

시행착오가 밑거름이 되는 공간

[cs231n] Training Neural Networks - part 1

업데이트:

개요

png

지금까지 neural network가 어떻게 동작하고 학습되는지에 대한 전반적인 내용을 살펴봤다면, 이번 포스팅은 본격적으로 training을 하는데 필요한 세부적인 기법들에 대한 내용이다. Part1 은 Activation functions, Data Preprocessing, Weight Initialization에 대한 내용이 포함된다.


Activation Functions

sigmoid를 사용하지 않는 이유

이전 포스팅에서 sigmoid function에 대해 다뤘다.
output은 [0,1]의 확률 값으로 도출되어 해석이 용이한 장점이 있었다.

그러나 최근에는 거의 사용하지 않는데, 크게 3가지 이유가 있다.

  1. Saturated neurons kill the gradients.
  2. Sigmoid outputs are not zero-centered.
  3. exp() is computationally expensive.

하나씩 자세하게 살펴보자.

1. Saturated neurons kill the gradients.

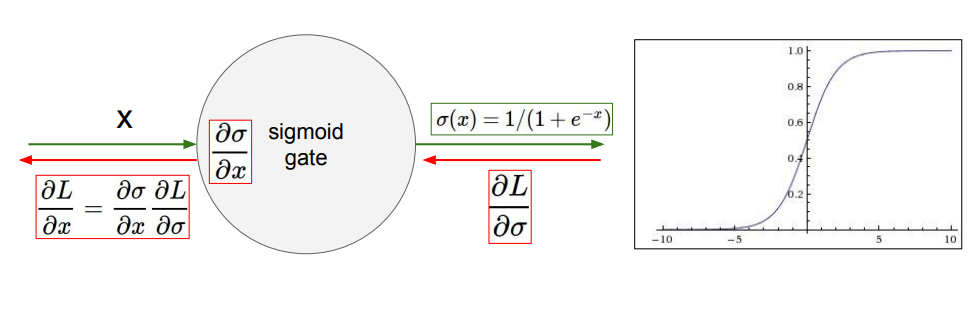
아래 그림을 보면 sigmoid function은 x축 0을 기준으로 양 또는 음의 방향으로 커질때 기울기(gradient)는 0에 수렴한다. 이를 “saturated 하다” 라고 표현한다.

png

이런 현상은 backpropagation의 관점에서 문제가 된다.
backpropagation은 upstream ($ \frac{\partial L}{\partial \sigma} $)와 local gradient ($ \frac{\partial \sigma}{\partial x} $)를 곱해서 뒤로 전파시킨다고 했었다.
그래서 input $ x $ 의 절대값이 어느정도 크게 들어오면 local gradient가 0이 돼버리고, 연쇄적으로 앞 node들은 upstream으로 0을 받는 구조가 된다. sigmoid layer가 더 존재한다면 계속 반복된다.
즉, gradient가 0이 되어 weight이 업데이트가 안되는 심각한 문제가 생긴다.

2. Sigmoid outputs are not zero-centered.

두번째는 sigmoid output이 평균이 0으로 고르게 분포(zero-centered)하고 있지 않은 문제가 있다는 것이다(sigmoid output은 [0,1]값을 갖는다).

png

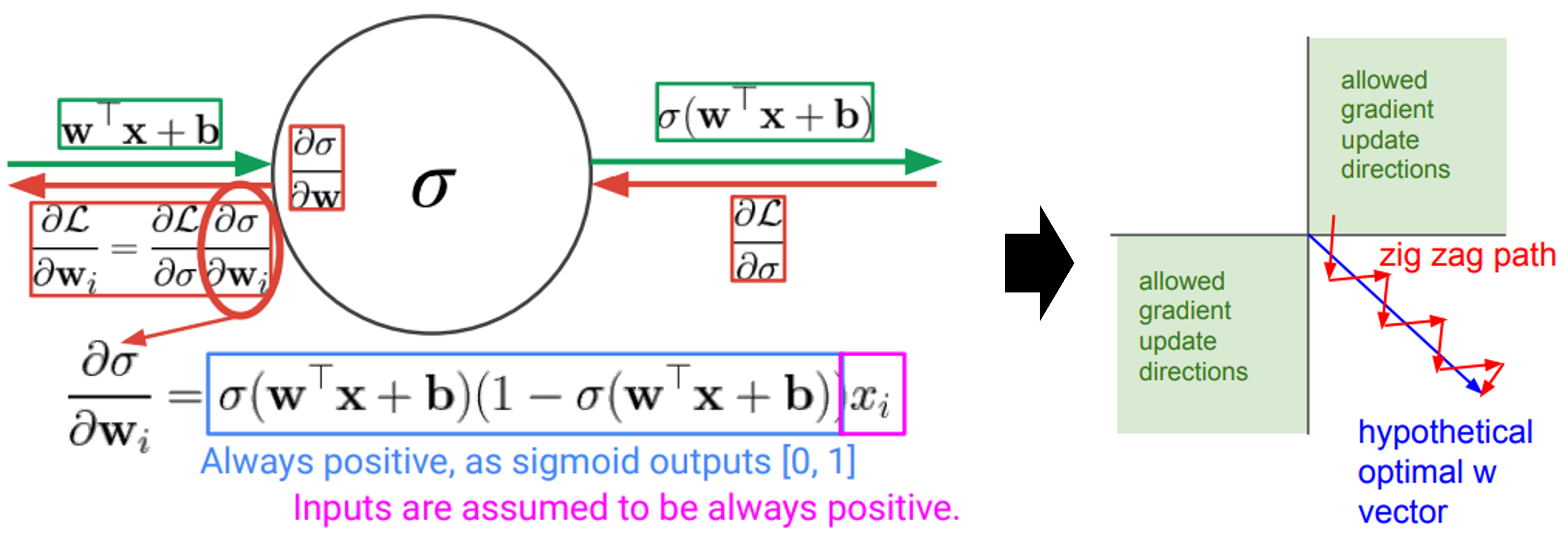
input $ x $가 항상 양수라고 가정해보자 (ex. 평점, 나이, 키 등 여러가지가 해당 됨).
그림(왼쪽)을 보면 sigmoid function의 local gradient 계산을 보여준다.
local gradient의 파란색 네모는 sigmoid output이 [0,1]임에 따라 항상 양수이므로, downstream ($ \frac{\partial L}{\partial w_i} $ )은 upstream ($ \frac{\partial L}{\partial \sigma} $)과 부호가 항상 동일하다.

\[\frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial \sigma}*(poisitive)\]

즉, upstream에 따라 모든 gradient의 element의 부호가 양수 또는 음수가 된다.
가정한 것 처럼 input $ x $가 모두 양수라면, 모든 gradient들의 부호는 바뀌지 않는다.
이게 왜 문제가 될까??

(오른쪽 그림) 항상 같은 부호를 가진다는 것은 weight이 2개라고 가정했을때 둘다 양수 또는 음수가 될 것이다. 이는 2차원 평면상에 1과 3사분면에 해당하는 방향으로만 weight을 업데이트할 수 있다는 것을 의미한다.
zig zag로 밖에 없데이트하지 못한다면, optimal한 path로 갈수 없기 때문에 비효율 적인 문제가 생긴다.

3. exp() is computationally expensive.

sigmoid function의 exp()연산이 상대적으로 컴퓨팅 비용이 많이 든다는 점에서 단점으로 작용한다.

이러한 단점들을 보완하기 위한 다양한 시도들을 기반으로 activation function들이 생겨나고 있다.
따라서 새로운 activation function들을 이해하려면, 기존에 어떤 단점들이 있었는지 명확하게 이해해야할 필요가 있다.

tanh (Hyperbolic Tangent)

tanh는 sigmoid와 유사하게 생겼다.

  • output이 [-1,1]으로, zero centered하다.
  • sigmoid 처럼 양 극단에서 saturated 하기 때문에 killing gradients 문제가 여전히 존재한다.
  • tanh의 수식은 실제로 sigmoid function을 약간 scaling 한 함수이다.

png

\[tanh(x)=2\sigma(2x)-1\]

ReLU (Rectified Linear Unit)

최근 가장 많이 사용되는 함수는 ReLU이다.

  • 양수인 구간에서는 saturated 한 문제가 없다.
  • 계산이 매우 효율적이다.(gradient는 양수는 1, 아니면 0)
  • 따라서 practical한 측면에서도 수렴속도가 빠르다.

하지만 ReLU도 문제점들이 존재한다.

  • Zero-centered하지 않은 문제는 여전히 존재한다.
  • x=0에서 미분이 불가능(not differentiable)하다.
  • Dead ReLU Problem: initial output이 음수면 해당 node는 영원히 update가 되지 않는다.

png

\[f(x)=max(0,x)\]

앞서 얘기한 Dead ReLU problem이 ReLU의 가장 치명적인 문제로, 원인은 크게 두가지가 있다.

  • Weight initialize를 잘 못한 경우
    • 애초에 negative한 region으로 초기화되면 Dead ReLU 문제가 발생한다.
  • Learning rate을 너무 크게잡은 경우
    • 초기 weight은 적절하더라도, learning rate이 너무 크면, saturated 하는 쪽으로 넘어가 버리면 다시 Dead ReLU 문제가 발생함

이를 위해 ReLU 초기화 시, 약간의 positive bias(e.g. 0.01)를 추가하기도 한다.
하지만 여전히 크게 도움은 안된다는 의견이 많다.

Leaky ReLU

Leaky ReLU는 앞선 ReLU의 문제점들을 보완하였다.

  • 음수 구간에 0.01값을 주어서 0으로 saturated 하는 문제를 방지한다.
  • 따라서 Dead ReLU problem을 해결한다.
  • 다른 ReLU의 장점들도 여전히 갖고 있다.

png

여기에서 0.01이라는 값도 데이터로부터 학습하겠다는 아이디어로 일반화 된 것이 PReLU(Parametric Rectified Linear Unit)이다.
Leaky ReLU의 0.01값을 $ \alpha $라는 parameter로 바꾸고, backpropagation을 할때 같이 학습되는 특징이 있다.

ELU (Exponential Linear Unit)

ELU도 마찬가지로 ReLU의 단점을 보완한 activation function이다.

  • ReLU의 모든 장점을 갖는다.
  • 수학적으로 mean이 zero가 되도록 만들었다(zero-centered).
  • Leaky ReLU와 달리 음수 구간을 saturated 하게 디자인하여, 너무 음의 값이 그대로 커지는 문제를 방지한다 (노이즈에 robust하도록).

하지만 앞서 얘기한 바와 같이 exp()연산은 여전히 컴퓨팅 효율이 떨어지는 문제가 있다.

png


지금까지 여러가지 activation function들을 살펴보았다.
강의에서는 실제로는 다음과 같이 사용할 것을 권장하고 있다.

  • 웬만하면 ReLU를 쓰고 Learning rate을 신경쓰자.
  • 필요 시 Leaky ReLU, ELU도 시도해 보자.
  • tanh, sigmoid는 쓰지말자.

png


Data Preprocessing

model에 넣을 input data를 어떻게 전처리할 것인지에 대한 내용을 다룬다. garbage in garbage out이라는 말이 있듯이 model의 tuning도 중요하지만 가장 중요한건 input data의 품질이다.

zero-centering & Normalization

여기서는 Zero-centering과 Normalization에 대해 알아보자.

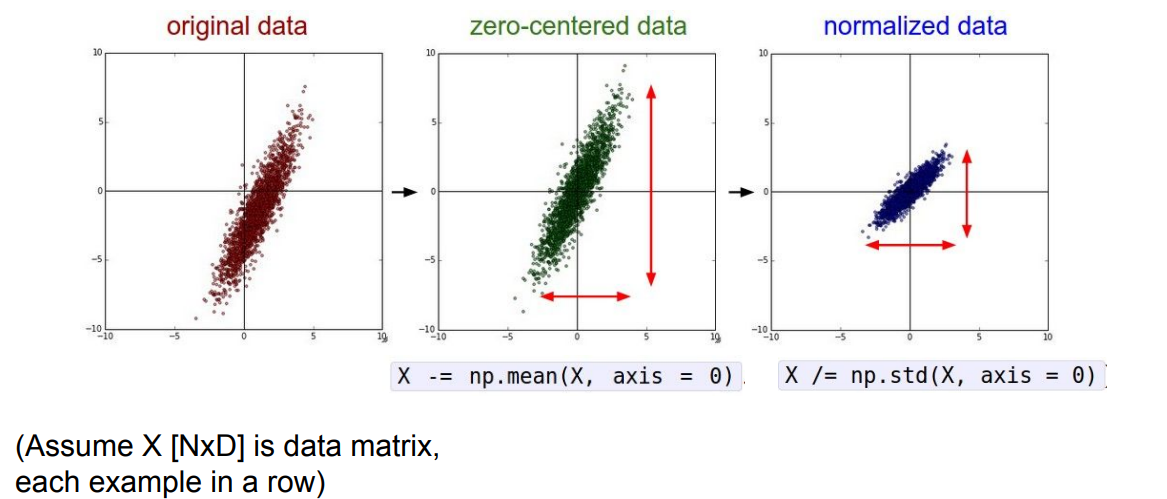
아래 그림과 같이 Zero-centering은 평균이 0이 되도록 모든 데이터들에서 평균값을 빼주는 과정이고, Normalization은 모든 축에 대해 scale이 같아지도록 표준편차로 나누어주는 과정이다.

png

Zero-centering을 하는 이유는 앞서 activation function에서 살펴봤던 not zero-centered 문제를 해결하기 위함과 같은 맥락이다.
(zig-zag path로 업데이트 되어야 하는 문제)

Normalization은 변수들의 단위에 따른 변화량(scale)이 큰 의미가 없을 때, 이러한 영향을 제외하기 위함이다(ex. 1달러과 1000원에서 1000원이 1000배 중요하다는 의미는 아니니까.?).

일반적으로 이미지 학습에서는 [0,255] 값의 분포와 pixel size가 비교적 균일하기 때문에, zero-centering만 수행한다.

PCA & whitening

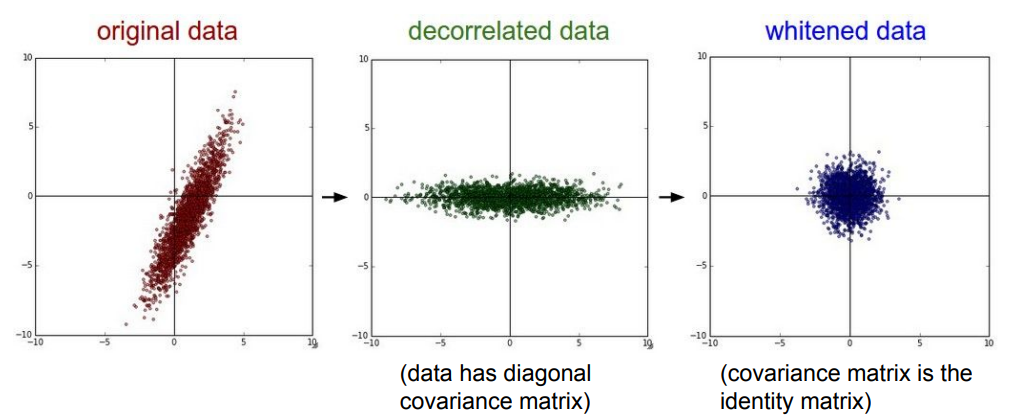
다른 방법으로는 주성분 분석이라고 하는 PCA(Principal Component Analysis)와 whitening이 있다.

아래 그림과 같이 PCA는 zero-centering을 하고 axis-align을 통해 decorrelate하게 만드는 원리이고, 그 다음에 whitening을 통해 scale를 맞추면 정규분포의 형태로 바꿀 수 있게 된다.

png

PCA의 과정을 간략하게만 적어보면,

  1. zero-centering을 먼저 한다.
  2. data의 covariance matrix를 계산한다.
  3. covariance matrix를 기반으로 고유값 분해(eigen-value decomposition) 수행한다.
    • eigen vectors, eigen values 도출
    • eigen vectors를 eigen valued의 크기에 따라 decreasing하게 sorting
  4. 이때 상위 벡터들은 가장 분산이 큰 축(데이터를 잘 설명하는)이 된다.
  5. 상위 몇 개의 벡터만 선택하고 나머지는 버림으로써 dimension reduction을 수행한다.

이런 과정을 통해 기존 데이터 [NxD]를 잘 설명할 수 있는 k개의 차원만 선택 [Nxk]해서 학습의 효율을 높일 수 있게 된다.

whitening은 이렇게 선택된 k개의 차원에 대하여 eigen-value 값으로 모든 차원을 다시 나눔으로써 scale을 맞춰주는 과정이다. 이에 따라 데이터는 정규분포로 변환된다.

PCA는 pixel level에서는 잘 사용되진 않고, feature를 다룰때 주로 사용된다.


Weight Initialization

지금까지는 weight을 어떻게 업데이트 할 것인가에 대해 알아봤었다. 그러면 가장 처음에 초기화 하는 weight은 어떻게 해야할까??
그냥 random으로 줘도 별 문제가 없을 것 같지만, 생각보다 꽤나 중요한 요인이다.

background

  • 일단 0으로 넣어보자.

그러면 input값에 관계없는 동일한 output이 계속 나오게 된다.
또한 앞서 나온바와 같이 gradient가 업데이트가 안된다.

  • 정규분포로 넣어보자(작은 값).

이번엔 정규분포에서 샘플링된 값들에 작은 값이 되도록 0.01을 곱해본 경우다.
아래 코드에서 W = 0.01 * np.random.randn(d_in,d_out)에 해당한다.
activation function이 tanh인 hiden layer가 있을 때, layer가 쌓일 수록 어떻게 되는지 관찰하기 위한 코드이다.

import numpy as np
import matplotlib.pyplot as plt
dims=[4096]*7
hs={}
x=np.random.randn(16,dims[0])
i=1
for d_in, d_out in zip(dims[:-1],dims[1:]):
    W = 0.01 * np.random.randn(d_in,d_out)
    x = np.tanh(x.dot(W))
    hs[i]=x
    i+=1

plt.figure(figsize=(14,3))
for i,H in hs.items():
    plt.subplot(1,len(hs),i)
    plt.hist(hs[i].ravel(), 30, range=(-1,1))

png

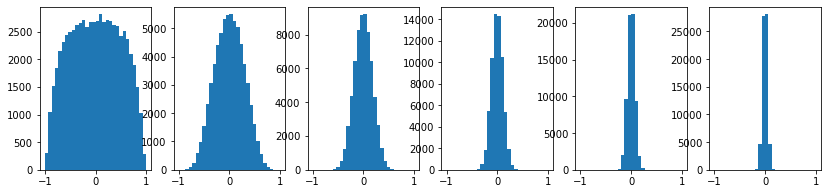
위의 결과 그래프를 보면, layer가 쌓여갈수록 대부분의 output 값들이 0으로 수렴하는 문제를 볼 수 있다.
이는 초기화된 weight값이 이미 작을 뿐아니라, tanh는 zero-centered하므로 0에 가까운 input이 들어오면 output도 0에 가까워 지기 때문이다.
이런 과정이 layer가 쌓이면서 반복되다보면 결국 output들이 0이되고, 결국 gradient들도 0이 된다.

  • 정규분포로 넣어보자(큰 값).

이번에는 동일한 코드에서 W = 0.5 * np.random.randn(d_in,d_out)로 변경해보자.

png

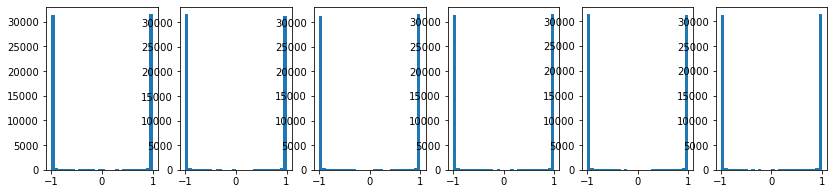
이번에는 큰 값의 input들은 tanh의 saturated한 구간으로 진입하게 되어 대부분 +1 또는 -1 값을 갖게 된다.
이 경우에도 saturated 한 구간에 도달하므로, gradient들이 0이 된다.

Xavier Initialization

사람들은 정규분포에 어느정도 크기의 값을 곱해주어야할까?? 라는 의문을 갖게된다.
대표적인 방법은 Xavier initialization으로 data 수의 제곱근으로 나누어주자는 아이디어를 실험적으로 발견하게 되었다.

코드에 W = np.random.randn(d_in,d_out)/ np.sqrt(d_in)를 넣고 다시 수행해보자.

png

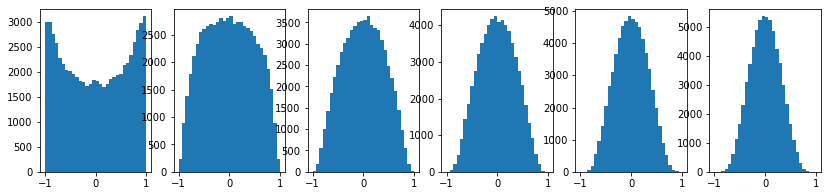
즉, data가 많아질수록 더 큰 값으로 나누어준다는 것이다.
일반적으로 output 값들은 input의 개수가 많아질수록 분산이 커지는 경향이 있기 때문에, 이러한 방식으로 scaling이 가능해 진다.

Xavier 논문에서는 통계학적 측면의 증명도 제공하고 있다.
개략적으로만 이해해보자.

우선 linear한 model $ y=Wx $가 있고, dimension은 다음과 같다고 가정해보자.
$ x \in \mathbb{R}^{d_{in}} $, $ W \in \mathbb{R}^{d_{out} \times d_{in}} $, $ y=Wx \in \mathbb{R}^{d_{out}} $

$ y_i=W_i^Tx=\sum_{j=1}^{d_{in}} W_{ij}x_j $

$ \Leftrightarrow Var[y_i]=Var[\sum_{j=1}^{d_{in}} W_{ij}x_j] $ $ (\because Var[X+Y]=Var[X]+Var[Y]) $

(가정: W와 x는 independent하다.)

$ \Leftrightarrow \sum_{j=1}^{d_{in}} Var[W_{ij}x_j] = d_{in} Var[W_{ij}x_j]$

(가정: W와 x는 identically distributed하다.)

두 가정을 합쳐서 i.i.d assumption 이라고 함

$ \Leftrightarrow d_{in} Var[W_{ij}x_j] = d_{in} (E[W_{ij}^2x_j^2] - E[W_{ij}x_j]^2) $ $ (\because Var[X]=E[X^2]-E[X]^2) $

$ \Leftrightarrow d_{in} (E[W_{ij}^2x_j^2] - E[W_{ij}x_j]^2)=d_{in} (E[W_{ij}^2]E[x_j^2] - E[W_{ij}]^2E[x_j]^2) $ $ (\because E[XY]=E[X]E[Y]) $

$ \Leftrightarrow d_{in} (E[W_{ij}^2]E[x_j^2] - E[W_{ij}]^2E[x_j]^2)=d_{in} (Var[W_{ij}]Var[x_j])$

(가정: 데이터나 weight모두 zero-centering을 했다고 가정하므로, $E[x]=E[W]=0$)

$ \therefore Var[y_i]=d_{in} (Var[W_{ij}]Var[x_j])$

최종 수식에서 input variance $ Var[y_i] $ 와 output variance $ Var[x_j]$ 가 같아지려면, 결국 weight은 $ Var[W_{ij}]=\frac{1}{d_{in}} $이 된다.
따라서 표준편차는 variance의 제곱근을 취하여 정규분포에 곱해주는 것이다.

He Initialization

지금까지는 tanh에 대해서만 실험을 했었다. 그러면 자주 사용된다는 ReLU에도 잘 될까??
np.tanh(x.dot(W)) 대신 np.maximum(0, x.dot(W))로 교체해보자.
차원을 유지하면서 두 array간 max값을 도출하는 np.maximum을 사용해야한다.

png

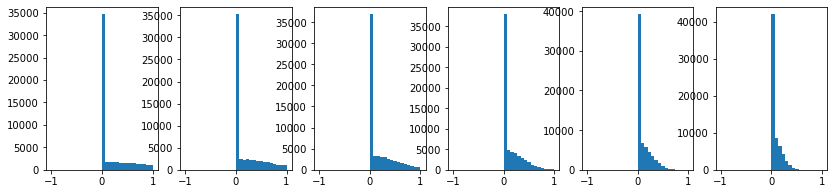
앞서 본것 처럼 ReLU는 0이하인 구간에서 gradient가 죽는 문제가 있었다.
우리가 생성한 평균이 0인 정규분포 data는 layer를 탈때마다 output을 절반씩 사라지게 만든다(0이 되어버린다).
그리고 0값이 된 x에 의해 gradient들도 0이되어 업데이트가 되지 않는다.

이러한 단점을 보완하고자 조금더 treatment를 준 것이바로 He initialization이다.
아이디어는 data 수의 절반에 대한 제곱근으로 약간 변형된다.
기존 코드에 W = np.random.randn(d_in,d_out)/ np.sqrt(d_in/2)로 변경하여 결과를 보자.

png

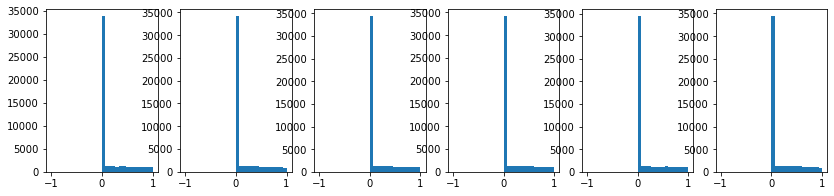
이렇게 하면 layer가 쌓이더라도 기존 분포가 잘 유지되고 있는 것을 확인할 수 있다.


Reference

이 포스팅은 cs231n 수업(by Prof. Li Fei-Fei at Stanford University)과 Machine Learning for Visual Understanding (by 서울대학교 이준석 교수님) 수업을 듣고 공부하며 작성하였습니다.

https://cs231n.github.io/

http://viplab.snu.ac.kr/viplab/courses/mlvu_2021_2/index.html

https://ai-rtistic.com/2021/10/29/cs231n-lecture6/

https://fabj.tistory.com/52

댓글남기기

참고