Yonggeun Shin

Yonggeun Shin

시행착오가 밑거름이 되는 공간

[cs231n] Neural Networks와 Backpropagation

업데이트:

개요

png

이번 포스팅에서는 deep learning의 기본 개념인 Neural networks의 기본 구조와 구성요소를 간단하게 알아보고, Loss를 통해 실질적으로 weight이 업데이트되는 과정인 Backpropagation에 대해 알아보자.


Neural Networks

Perceptron

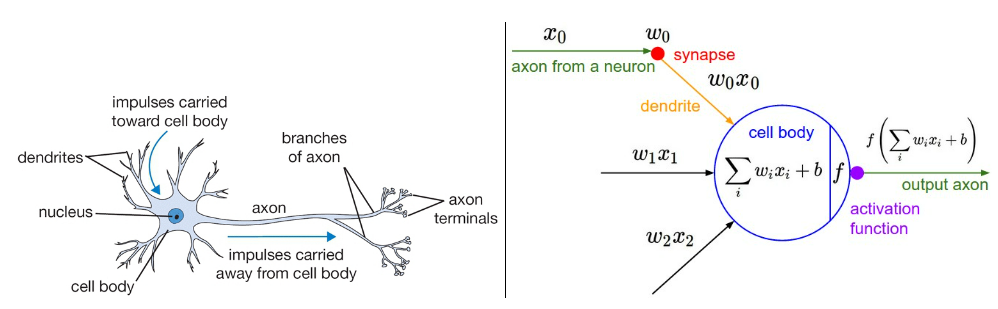
신경망을 얘기하면 뉴런을 닮아있는 퍼셉트론(Perceptron)에 대한 얘기가 먼저 나온다.

png

이것은 사실 이전에 포스팅한 linear classifier를 보기쉽게 표기한 것 뿐이다.

*하나 추가된 내용은 activation function에 한번 태워서 빼는 것인데, 이는 perceptron을 multi layer로 쌓게 될때 non-linearity를 반영하기 위한 treatment이다(MLP에서 설명하자).

MLP (Multilayer Perceptron)

따라서 위에서 설명한 linear form을 node형태로 나타낸 것이 결국 신경망이라고 생각할 수도 있다. 여기서 layer를 겹겹이 쌓는 것이 바로 MLP(Multilayer Perceptron)이다.

아래 그림 한장으로 모두 이해할 수 있다.

png

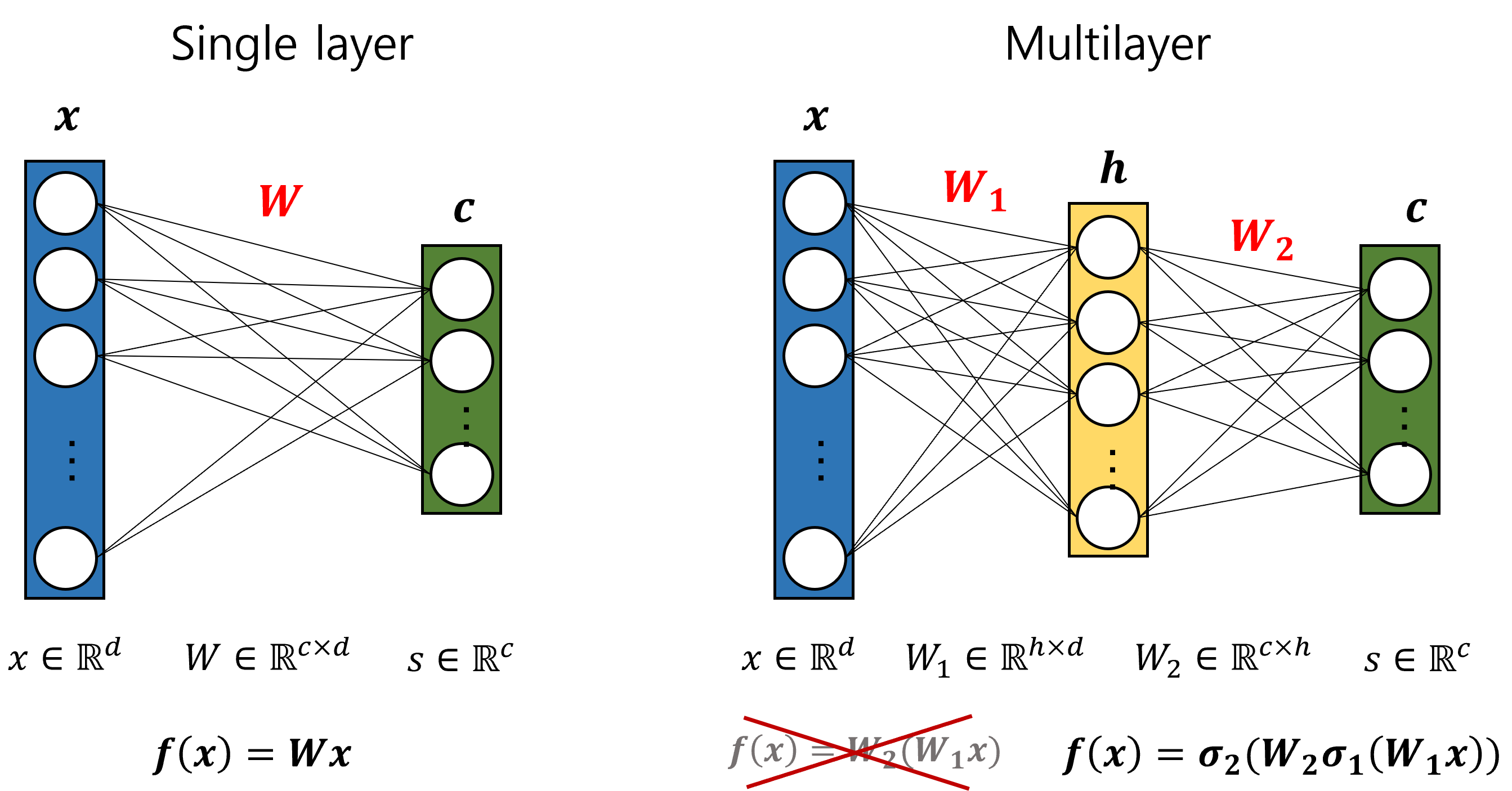
활성화 함수(Activation function)를 통해 non-linearity를 반영할 수 있는 이유는 행렬곱을 통해 알 수 있다.

그림에서 보는 것 처럼 input과 weight vector에 대한 연산은 행렬곱으로 이루어진다. Multilayer에서 layer을 쌓을때 활성화함수가 없으면 $ f(x)=W_2(W_1x)$ 가 되어 결국 single layer와 다를게 없어진다.

따라서 신경망이 나오게 된 계기라고도 할 수 있는 non-linear 문제를 다루려면 꼭 필요한 조건이라고 할 수 있다.

사용해볼 수 있는 activation function은 sigmoid나 ReLU, tanh 등이 있고 추후에 따로 다루기로 하자.


Backpropagation

경사하강법에서 얘기했던 것 처럼, Loss를 minimize하기 위하여 현재 시점에서 gradient를 계산하고 weight를 업데이트 해야 한다고 했었다. 그리고 gradient는 미분을 통해 구할 수 있었다. 즉, loss function에 대한 각 weight의 gradient가 필요하다.

\[\frac{\partial L}{\partial W_1}, \frac{\partial L}{\partial W_2}\]

위의 MLP에서의 gradient를 analytical하게 구해보자.

Loss와 MLP는 각각 $ L=(\hat y-y)^2 $와 $ \hat y = W_2\sigma (W_1x) $라고 하자.
우리가 구하고자 하는 gradient는 chain rule에 의해서 다음과 같이 계산된다.

\[\begin{align*} & \frac{\partial L}{\partial W_2}=\frac{\partial L}{\partial \hat y} \frac{\partial \hat y}{\partial W_2} = 2(\hat y-y)*\sigma(W_1x) \\ & \frac{\partial L}{\partial W_1}=\frac{\partial L}{\partial \hat y} \frac{\partial \hat y}{\partial h} \frac{\partial h}{\partial W_2} = 2(\hat y-y)*W_2*h(1-h)*x \quad (\because h=\sigma(W_1x)) \\ \end{align*}\]

그러나 모델이 복잡해질수록 수학적인 방식으로 미분하는건 불가능하다.
이런 이유로 생겨나게 된 것이 바로 역전파 (Backpropagation) 알고리즘 이다.

Simple example

backpropagation의 핵심은 chain rule이라고 볼 수 있다.
먼저 간단한 예제를 보자.

$ f(x,y,z)=(x+y)z $ 와 같은 함수가 있다고 했을때, 이를 computational graphs 로 나타내면 아래와 같다.

png

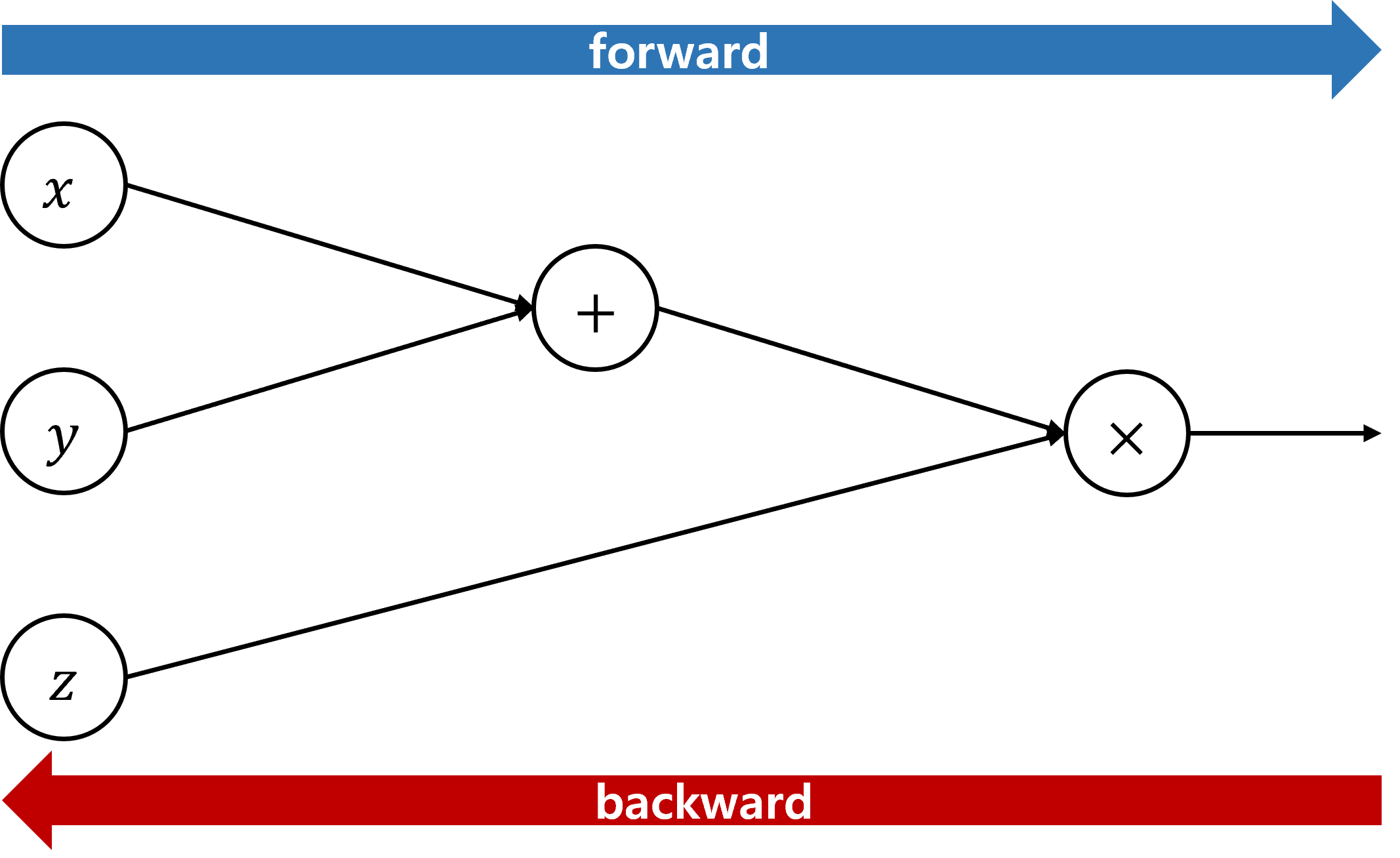
  • forward: input vector를 통해 Loss를 계산하는 과정
  • backward: loss를 기반으로 gradient를 계산하는 과정

input으로 $ (x,y,z)=(-2, 5, -4)$ 가 들어간다고 가정했을때, 우리는 최종 $f$ 값에 대해 $x,y,z$가 얼마나 기여했는지를 구하고 싶은 것이다. 다시 표기하면 아래와 같다.

png

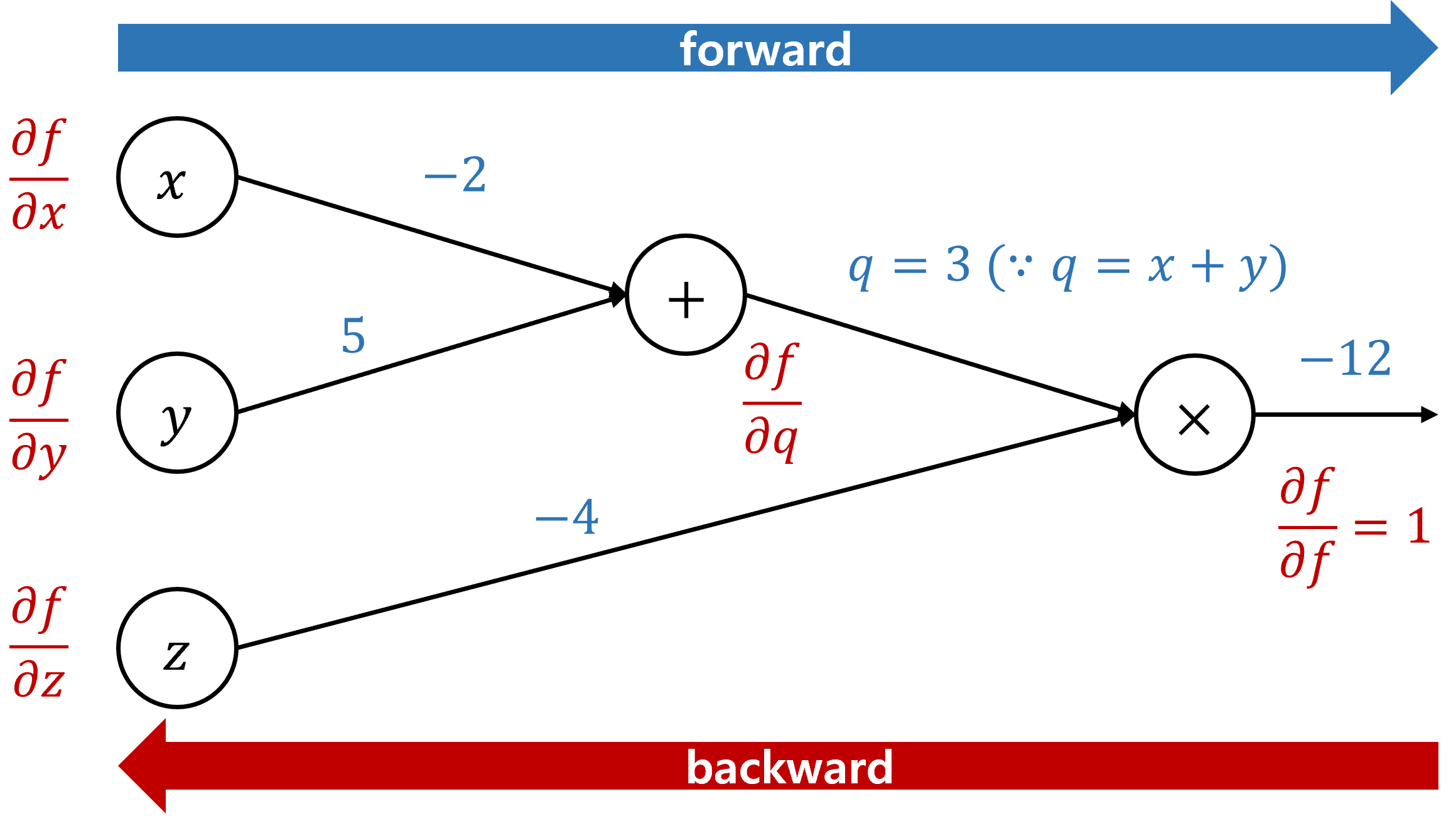
편의를 위해 $q=x+y$로 치환하였다. 가장 마지막 값은 자기 자신으로 미분하여 $\frac{\partial f}{\partial f}=1$ 이되고, 하나씩 역으로 전파된다.

\[\begin{align} & \frac{\partial f}{\partial z}=\frac{\partial (qz)}{\partial z}=q=3 \\ & \frac{\partial f}{\partial q}=\frac{\partial (qz)}{\partial q}=z=-4 \\ & \frac{\partial f}{\partial x}=\frac{\partial f}{\partial q} \frac{\partial q}{\partial x}=\frac{\partial (qz)}{\partial q} \frac{\partial (x+y)}{\partial x}=z*1=-4 \\ & \frac{\partial f}{\partial y}=\frac{\partial f}{\partial q} \frac{\partial q}{\partial y}=\frac{\partial (qz)}{\partial q} \frac{\partial (x+y)}{\partial y}=z*1=-4 \\ \end{align}\]

최종적인 backward gradient까지 표기해보자.

png

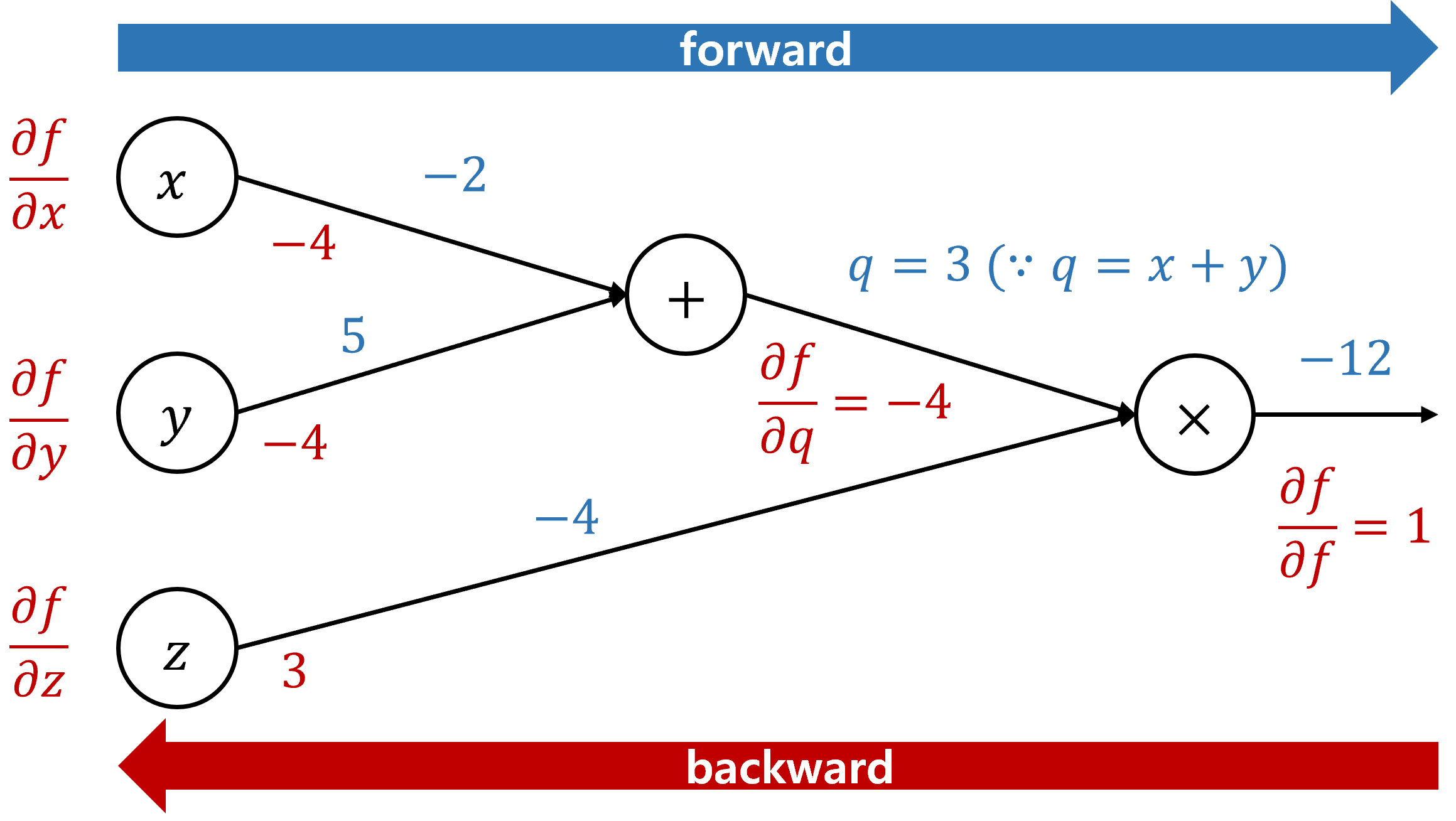
이렇게 제일 마지막 값부터 역으로 전파해야하는 이유는, chain rule을 적용하기 위해서는 뒤쪽에서 계산한 값이 필요하기 때문이다.

위 과정을 pytorch로 확인해보자. pytorch는 Autograd를 기반으로 backward를 할때 자동으로 미분값을 계산해준다.

import torch

x = torch.tensor(-2.0, requires_grad=True)
y = torch.tensor(5.0, requires_grad=True)
z = torch.tensor(-4.0, requires_grad=True)

f = (x+y)*z
f.backward()
print(x.grad, y.grad, z.grad)

tensor(-4.) tensor(-4.) tensor(3.)

Chain rule

Chain rule을 조금더 일반화된 형태로 이해해보자.
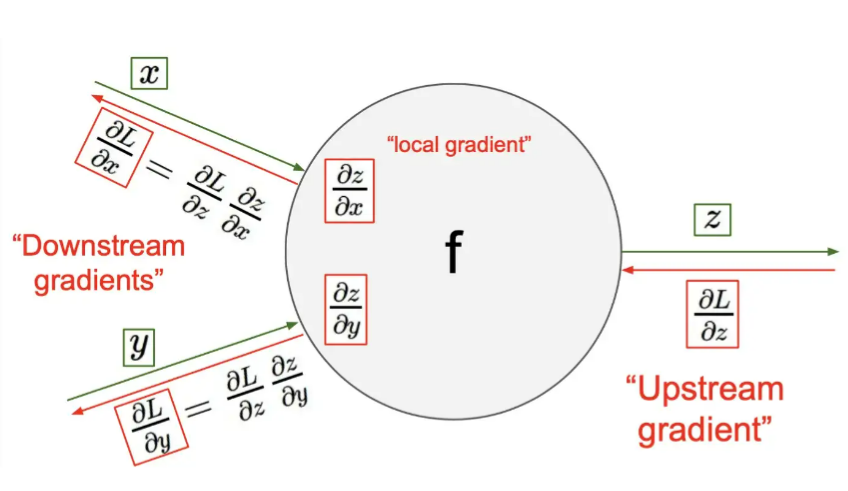
앞의 예제에서 직접 계산을 해봤는데, node 하나의 관점에서 forward와 backward의 규칙이 존재하는 것을 알 수 있다.

png

결론부터 얘기하면, 각 node마다 들어오는 input과 output간의 Local gradient만 계산하면 Upstream gradient와 곱해서 Downstream gradient로 나가게 된다.
앞의 예제에서 처럼 가장 마지막의 node는 항상 1이기 때문에, node마다 local gradient만 계산하고 곱하여 맨 앞으로 나아갈 수 있는 것이다.

Backward patterns

자주사용되는 연산들에서 chian rule에 의해 backpropagation 알고리즘이 적용될 때 발견할 수 있는 pattern들이 있다.

png

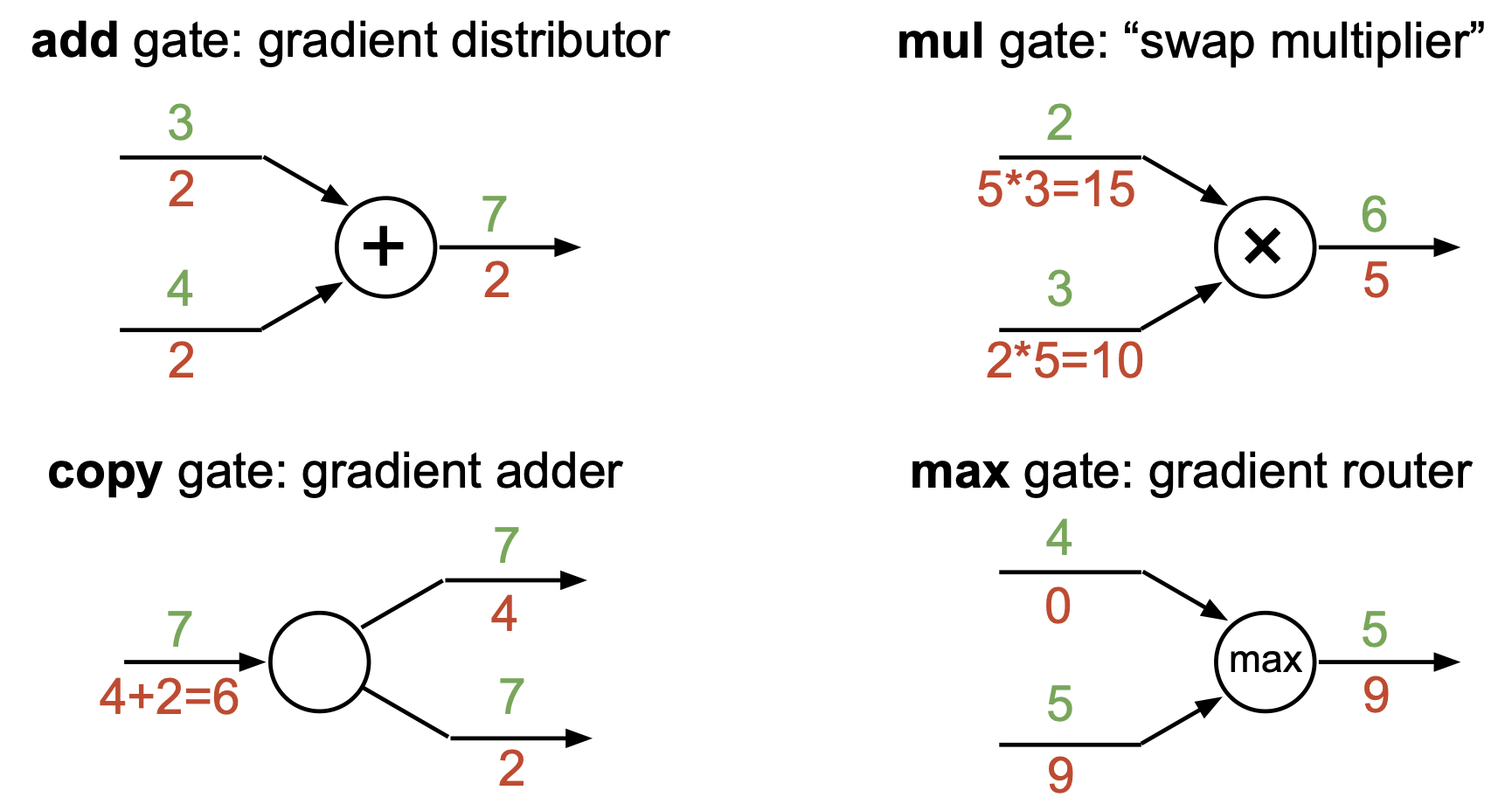
  • add gate: upstream gradient를 그대로 복사해서 downstream에 전달
  • mul gate: upstream gradient에 상대방의 input 값을 곱해서 downstream에 전달
  • copy gate: copy해서 forward로 나간 gradient들이 합쳐서 downstream에 전달
  • max gate: upstream gradient를 max값으로 지정됐던 쪽(argmax)에 그대로 전달, 나머진 0
    • 미분은 변화율을 의미하는데, max값이 아닌 쪽은 input이 달라져도 영향이 없기 때문임

Logistic regression

다른 예제로 이번에는 logistic regression에 대하여 backpropagation 알고리즘을 적용해보자.
주어진 함수에 대한 forward와 backward는 아래와 같이 나타난다.

\[f(x,w)= \frac{1}{1+e^{-(w_0x_0+w_1x_1+b)}}\]

png

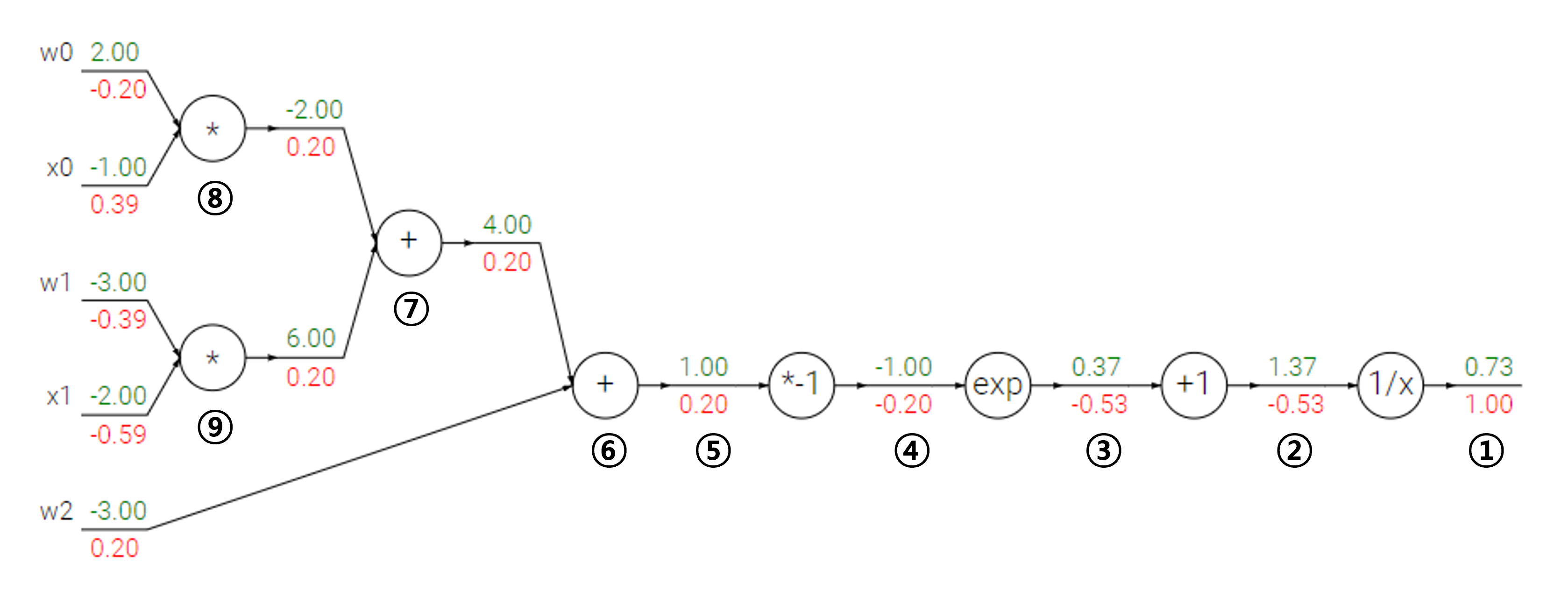
  1. 마지막 node의 gradient는 항상 1이다.
  2. $ f(x)=\frac{1}{x} $이므로, $ \frac{\partial f}{\partial x}=-\frac{1}{x^2}$
    • (upstream)(local) = $(1.00)(-\frac{1}{1.37^2})=-0.53$
  3. $ f(x)=x+1 $이므로, $ \frac{\partial f}{\partial x}=1$
    • (upstream)(local) = $(-0.53)(1)=-0.53$
  4. $ f(x)=e^x $이므로, $ \frac{\partial f}{\partial x}=e^x$
    • (upstream)(local) = $(-0.53)(e^{-1})=-0.20$
  5. $ f(x)=-x $이므로, $ \frac{\partial f}{\partial x}=-1$
    • (upstream)(local) = $(-0.20)(-1)=0.20$
  6. add gate에 의해 같은 값으로 downstream에 전파
  7. add gate
  8. mul gate에 의해 upstream gradient에 상대방의 input 값을 곱해서 downstream에 전달
  9. mul gate

이렇게 구해진 각 weight들은 gradient를 기반으로 업데이트 된다.

\[w_i^{new}=w_i^{old}-\alpha (\frac {\partial L}{\partial w_i})\]

vectors 역전파

지금까지 모든 차원이 scalar인 경우에 대해 알아봤지만, 실제로는 input과 output이 vector또는 metrix인 경우로 확장된다. 이때 Jacobian Matrix를 사용한다.

Jacobian Matrix는 모든 벡터들의 1차 편미분 값으로 이루어진 행렬을 의미한다.
아래 그림에서 local gradient를 계산할때, $[D_x \times D_z] $와 $[D_y \times D_z] $ 차원으로 이루어진 두개의 자코비안 행렬을 계산하게 된다.
즉, scalar와 같은 맥락에서 변수들 간의 gradient를 계산하여 넘겨준다 얘기다.
곱해서 downsteam으로 나갈땐 행렬곱을 통해 나간다.

jpg

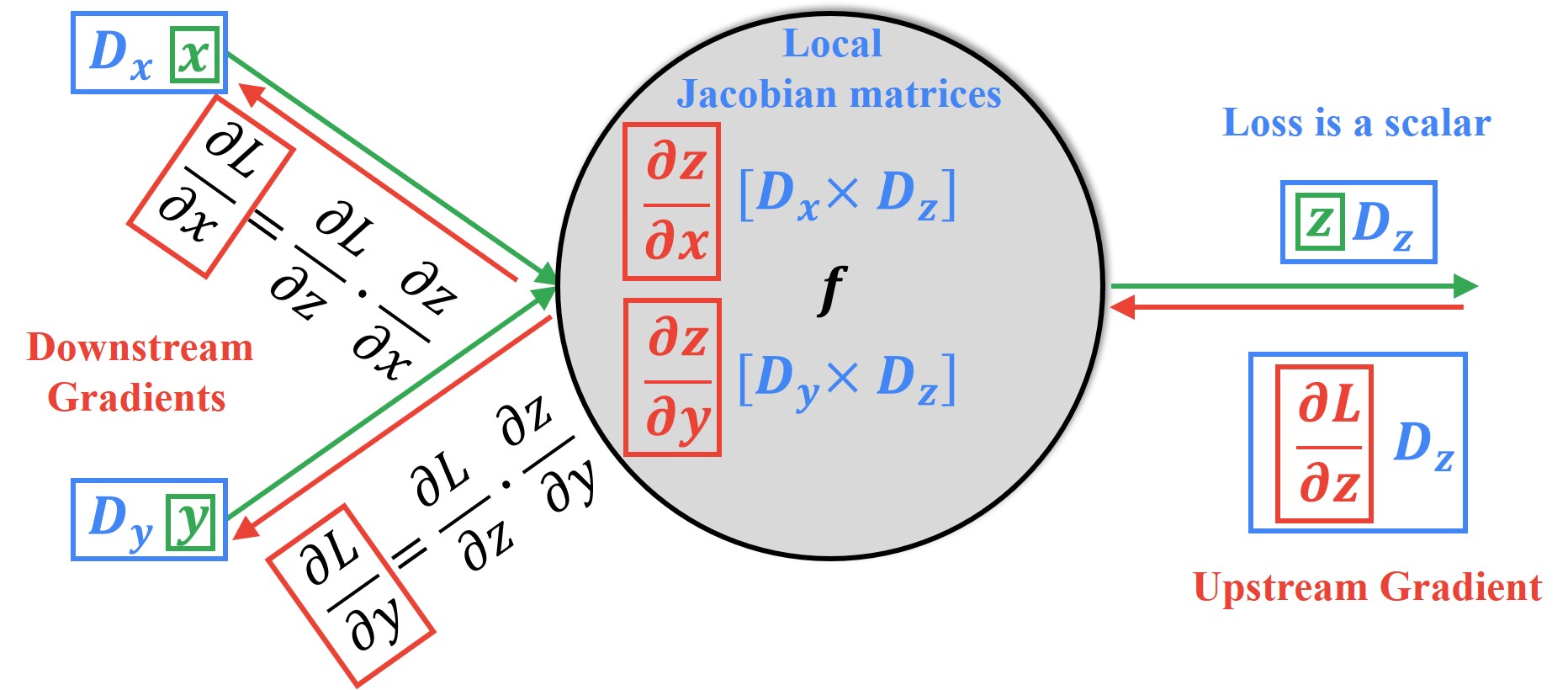
헷갈릴 수 있지만, 결국 Upstream과 Downstream으로 나가는 gradient들의 차원은 기존 forward의 variable이 가졌던 차원과 동일해야 한다.

Matrix에 대한 역전파는 차원이 하나 더 커지지만, 같은 맥락으로 이해할 수 있다.


Reference

이 포스팅은 cs231n 수업(by Prof. Li Fei-Fei at Stanford University)과 Machine Learning for Visual Understanding (by 서울대학교 이준석 교수님) 수업을 듣고 공부하며 작성하였습니다.

https://cs231n.github.io/

http://viplab.snu.ac.kr/viplab/courses/mlvu_2021_2/index.html

https://ganghee-lee.tistory.com/30

https://datahacker.rs/009-pytorch-how-to-apply-backpropagation-with-vectors-and-tensors/

https://gaussian37.github.io/math-calculus-jacobian/

댓글남기기

참고