Yonggeun Shin

Yonggeun Shin

시행착오가 밑거름이 되는 공간

[cs231n] Loss function과 Optimization

업데이트:

개요

png

우리는 이전 포스팅의 Linear classifier에서 input image와 가중치 연산을 통해 label간의 최종 score를 산출했다.
이에 따라 생기는 두가지 물음에 대한 답이 이번 포스팅의 내용이다.

  • Loss function : 그 score가 어느 정도의 성능을 나타내는건지?
  • Optimization : 더 좋아지려면 어떻게 해야하는지?


Loss function

Loss function은 현재 model이 얼마나 좋은 예측을 하고 있는지를 정량적으로 확인할 수 있는 지표이다.
따라서 Loss function은 True 값이 $y$이고 predict 값이 $\hat{y}$ 일 때의 $L(y,\hat{y})$ 이다.

이는 model이 개선되어야하는 정도라고 이해할 수 있다.
즉, $y$와 $\hat{y}$이 같아질수록 0에 가까워야하며, 반대일수록 커지는 형태이어야할 것이다.

Margin-based와 Distance-based

Loss function을 배우기 앞서, $y$와 $\hat{y}$이 다른 정도를 나타내는 방법을 정의할 필요가 있을 것이다.

Margin-based loss는 $y\hat{y}$ 형태로 부호를 기반으로 정량화하는 방법이다. 이진분류(binary classification)에서 $y={+1,-1}$이라고 할때 아래와 같이 정의된다.

  • $y\hat{y}$ > 0 이면, 맞게 예측을 한 것이 될 것이고
  • $y\hat{y}$ < 0 이면, 부호가 다르므로 틀린 것이다.

자세한 내용은 여기를 참고하자.

distance-based loss는 $y-\hat{y}$ 형태로 실제값과 예측값의 차이를 기반으로 정량화하는 방법이다.

이제 Loss function에 대해 알아보자.

Multiclass SVM Loss

Hinge Loss라고도 불리는 Multiclass SVM(Support Vector Machine) Loss가 있다(Margin-based loss로 설명).

먼저 binary classification 문제에서 margin-based loss로 표기된 hinge loss를 확인해보자.

png

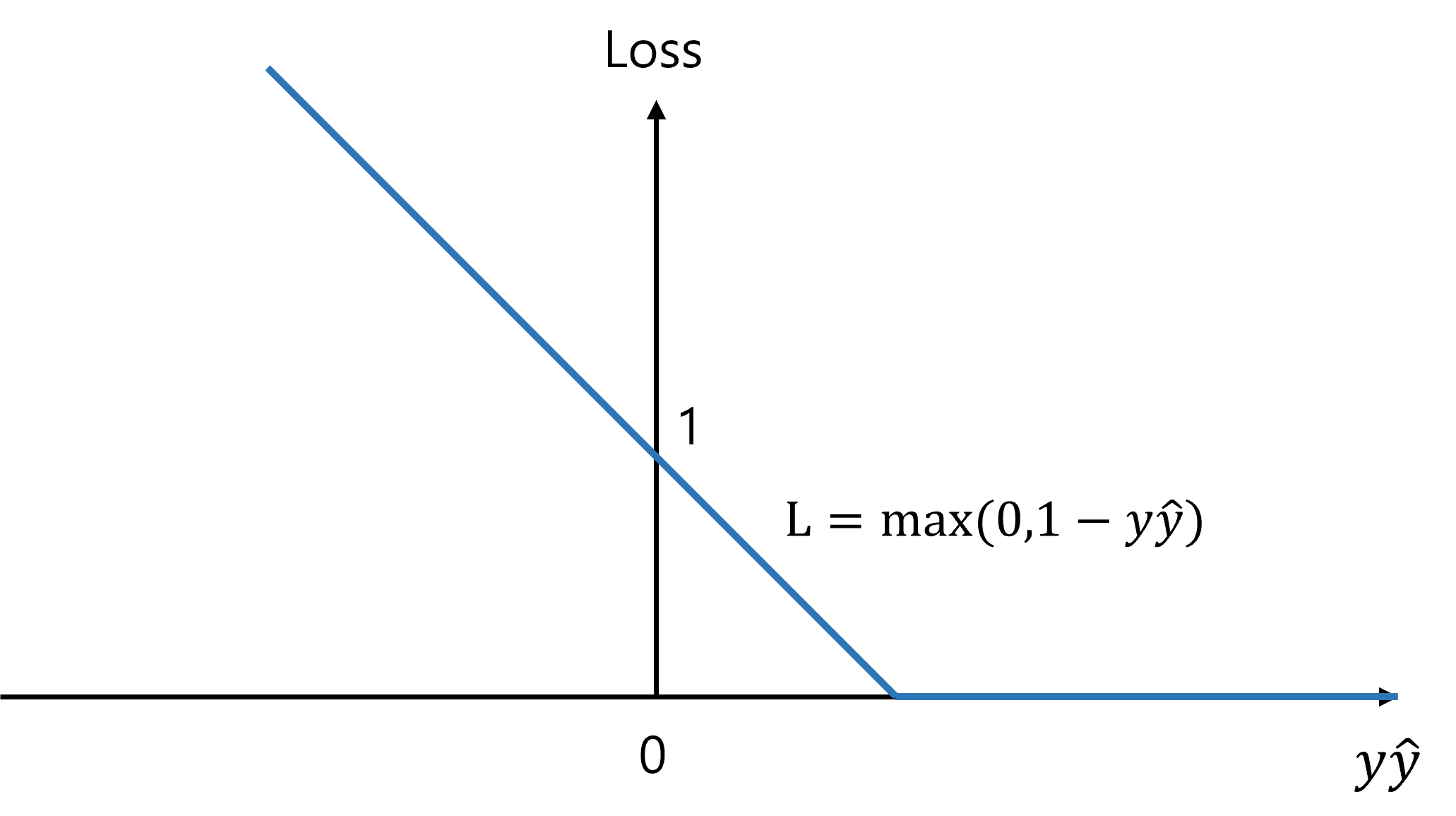
Idea는 Margin이라는 개념을 도입해서(위 그림에서는 margin=1), Margin 보다 큰 값으로 예측할때만 Loss를 0으로 주고 그 외에는 비례해서 loss가 커진다.

class가 여러개인 문제에서는 distance-based loss로 다음과 같이 일반화된다.

\[\begin{align*} L_i&=\sum_{j\neq y_i} \begin{cases} 0 \qquad\qquad\qquad\; if \quad s_{y_i}\geq s_j+1 \\ s_j-s_{y_i}+1 \qquad otherwise\\ \end{cases} \\ & \\ & = \sum_{j\neq y_i} max(0, s_j-s_{y_i}+\Delta) \end{align*}\]

여기서 $\Delta$ 는 margin을 의미하며, $s_{y_i}$와 $s_j$는 이미지 $i$에 대한 예측 값들에서 정답 클래스와 정답이 아닌 클래스의 score들을 나타낸다.

따라서 car이라는 이미지 $i$에 대한 예측이 다음과 같을 때 loss $L_i$는 다음과 같다($\Delta=1$).

cat   car   airplane
1.3   4.9   2.0
\[L_i=max(0,1.3-4.9+1)+max(0,2-4.9+1)=0\]

즉, 한 이미지에서 정답으로 예측한 값 $s_{y_i}$가 정답이 아닌 값 $s_j$ 대비 margin $\Delta$ 보다 크게 확신(?) 할 경우에만 loss를 0으로 주겠다는 것이다.
이는 결국 margin이 클수록 정답이 오답 대비 score의 갭이 커져야한다는 (확실해야한다) 의미다.

따라서 epoch 마다의 최종 loss는 평균값으로 아래 수식과 같다.

\[L=\frac{1}{N} \sum_{i=1}^N L_i\]

Hinge Loss에서 특징을 조금 정리해보면 다음과 같다.

  • margin은 보통 1로 설정한다.
    • distance-based loss에서 가중치와 scale에 따라 점수차이가 달라지므로 margin의 크기가 큰 의미가 없는 경우가 많기 때문
  • 데이터에 민감하지 않다.
    • 위 수식에서 $s_{y_i}\geq s_j+1$ 를 만족하면 loss는 언제나 0이므로, 이때 score가 달라지는 것은 학습에 영향을 주지 않음
  • $j\neq y_i$ 인 경우만 보는 이유
    • 정답 클래스는 loss가 항상 1이 되기 때문에 제외해야함

Softmax classifier

지금까지는 linear classifier로 부터 도출되는 score 값에 대해 다뤘는데, 이 값은 절대적 수치가 뭘 의미하는지? 알기가 어렵다. (얼마나 확신한다는거야?)

(이전 포스팅에서도 다룬적이 있지만) 이러한 수치를 [0,1]의 확률값으로 변환시켜주는 sigmoid와 그 확장인 softmax에 대해 알아보자.

먼저 binary classification에서 class 1을 정답으로 예측하기 위한 loss는, 앞서 언급한 것처럼 $s_1-s_2$가 될 것이다.

이를 확률값으로 도출하기 위해 sigmoid function 대입해주면 아래와 같이 나타난다.

png

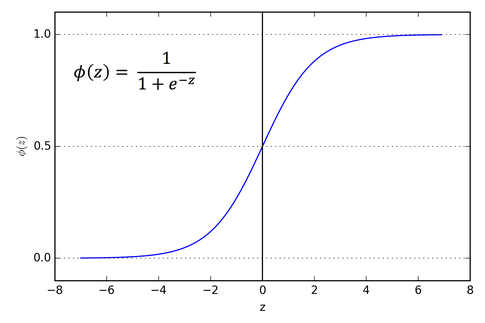
여기서 기존 score인 $s_1-s_2$를 대입해주고 아래와 같이 정리하면 확률형태로 도출된다.

\[p(y=c_1|X)=\frac{1}{1+\exp^{-(s_1-s_2)}} = \frac{e^{s_1}}{e^{s_1}+e^{s_2}}\] \[p(y=c_2|X)=\frac{1}{1+\exp^{-(s_2-s_1)}} = \frac{e^{s_2}}{e^{s_1}+e^{s_2}}\]
  • 모든 사건의 확률은 [0,1] 값을 가짐
  • 모든 사건에 대한 확률의 합은 1

결국 형태는 모든 class의 score에 각각 exponential을 씌운 값 대비 각 class의 값으로 변환되는 형태이다.

이를 class가 k(>2)개 일때로 확장한 것이 Softmax classifier이다.

\[p(y=c_i|X) = \frac{e^{s_2}}{e^{s_1}+e^{s_2}+...+e^{s_k}} = \frac{e^{s_i}}{\sum_j e^{s_j}}\]

Cross Entropy Loss

Cross Entropy Loss는 위와 같이 확률적(probabilistic)으로 score를 정의할 때에 대하여 loss를 정량화하는 방법 중 하나이다.

확률적으로 정의했다는 것은 다음과 같다.

  • $y$ True value : {0,1}
  • $\hat{y}$ predict value : [0,1]

즉, predict 값은 sigmoid 의해 확률값으로 도출되며, ground truth는 0또는 1의 값을 갖는다.
softmax일 경우는 y=[0,0,1,0,0,0] 와 같이, k개의 class중 true만 1로 표시되는 형태로 확장된다.

이미지 $N$장에 대한 Cross entropy loss는 다음과 같이 정의된다.

  • k class에 대한 일반적인 수식
\[L=-\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K y_{ik}log(\hat{y}_{ik})\]
  • Binary classification (k=1)에서의 수식
\[L=-\frac{1}{N} \sum_{i=1}^N [y_{i}log(\hat{y}_{i}) + (1-y_i)log(1-\hat{y}_{i})]\]

binary는 class가 2개 이므로, k에서 $y_i$와 $1-y_i$ 만 남게되기 때문이다.

일반적인 수식을 좀더 살펴보면, $y_ik$는 결국 ground Truth 값 1개만 1이기 때문에 나머지 0으로 사라지는 항을 제외하면 아래와 같이 단순해진다.

\[L=-\frac{1}{N}\sum_{i=1}^N log(\hat{y}_{iT_i})\]

$\hat{y}_{iT_i}$는 이미지 $i$에서 분류기가 groud truth에 대해 예측한 확률값이다.
즉, 실제 답에 해당하는 확률값을 얼마나 잘 맞췄냐는 것으로만 loss를 주겠다는 것이다.

추가적으로 위 수식에서 $-log$가 하는 역할을 알아보자.

png

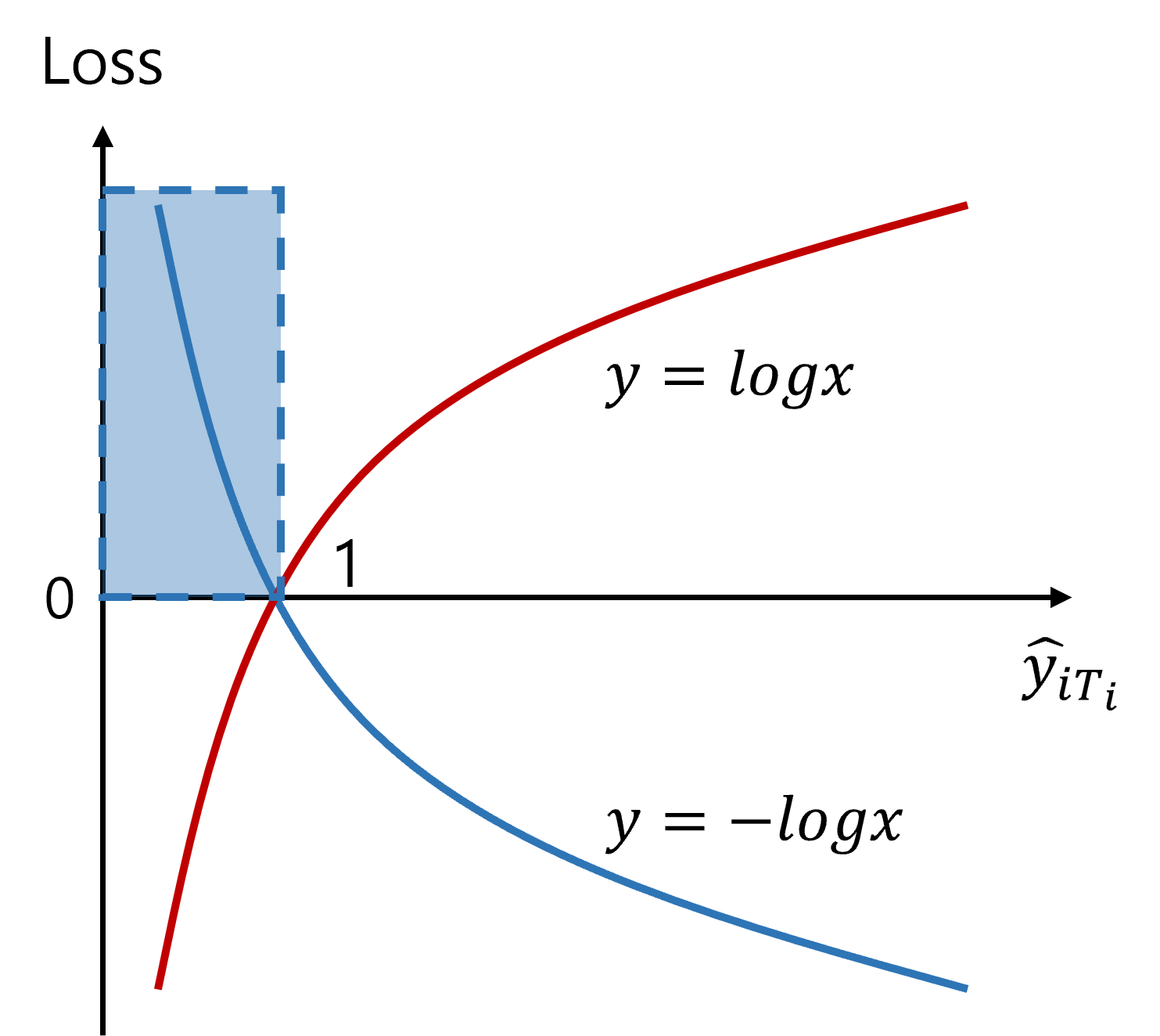
위 그림처럼 우리의 prediction들은 [0,1] 사이의 확률값으로 도출된다. $y=-logx$ 함수에 대입시키면, 1에 가까워질수록 loss가 작아지고 반대는 커지는 형태로 loss를 디자인할 수 있다.


Optimizer

지금까지 현재 학습 결과가 어느정도의 성능을 가지는지 정량화했다면, Optimizer는 더 좋아지려면 가중치를 어떻게 업데이트 해야할지 결정하는 최적화 문제이다.
이 자체는 매우 방대한 내용이지만, 여기서는 이전에도 다룬적 있는 경사하강법(gradient descent)의 개념만 잡고 넘어가도록하자.

gradient descent

우리는 loss function을 global하게 minimize하는 것이 궁극적인 목표이다. 그러나 실제로 도출되는 함수의 형태를 완벽하게 파악할 수 없기 때문에, heuristic하게 해를 찾아나가야 한다.

근데 이렇게 찾아나가는 방법을 산에서 하산하듯이 기울기(gradient)에 따라 방향을 결정하고, 그 방향으로 나아가는 것(learning rate)이 바로 경사하강법이다.

이를 설명하기 위한 그래프는 아래와 같이 나타난다.

png

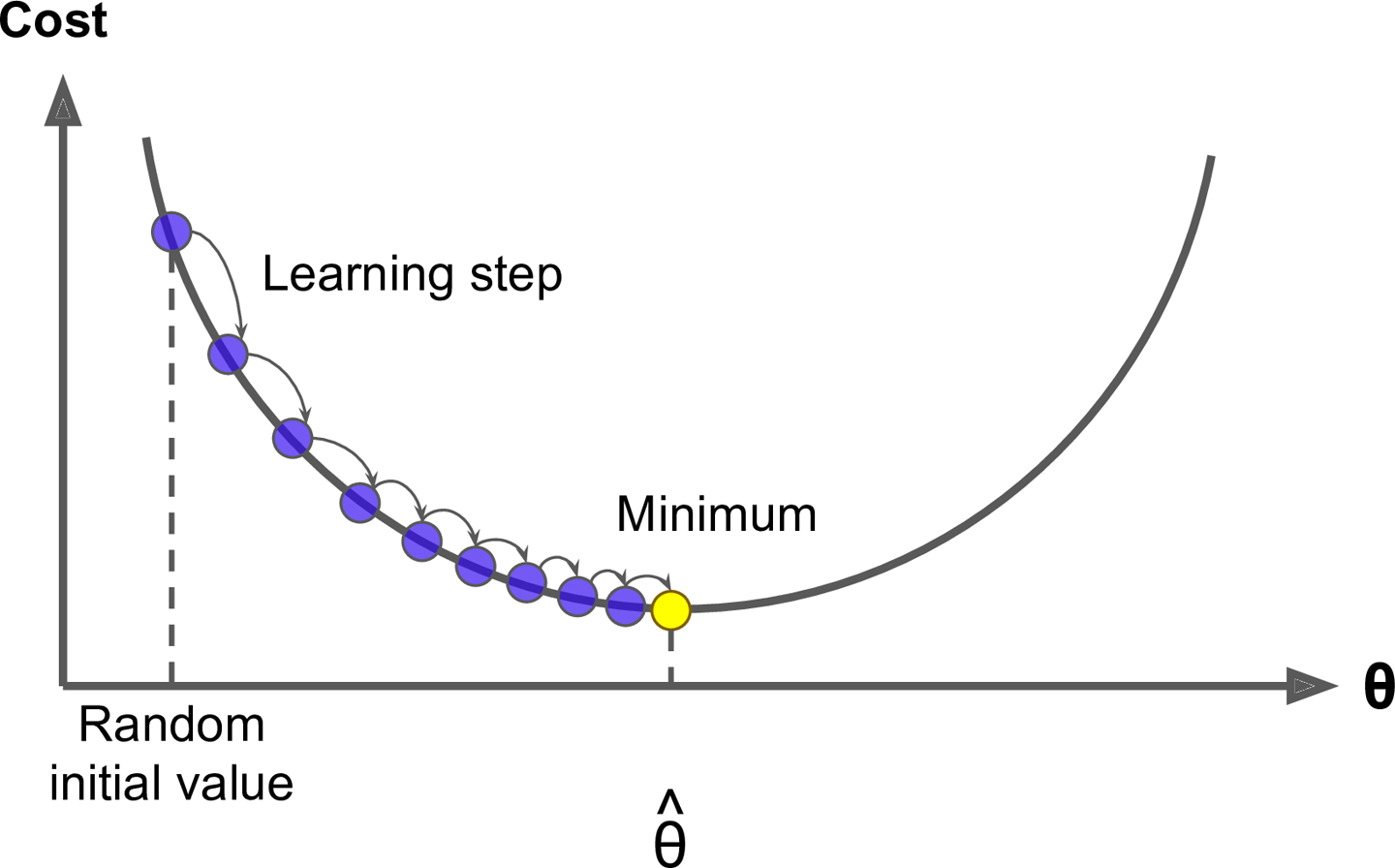
즉, model의 parameter인 $\theta$값들에 의해 정의된 cost $J(\theta)$가 minimum에 도달하도록 $\theta$ 를 찾게된다.

따라서 업데이트하기 위한 equation은 아래와 같다.

\[\theta^{new} = \theta^{old}-\alpha \bigtriangledown_\theta J(\theta)\]

*$\alpha$ 는 learning rate
*$-$인 이유는 gradient가 음수일땐 우측으로, 양수일땐 좌측으로 이동하기 위한 조치이다.

Challenge

png

Source : The journey of Gradient Descent

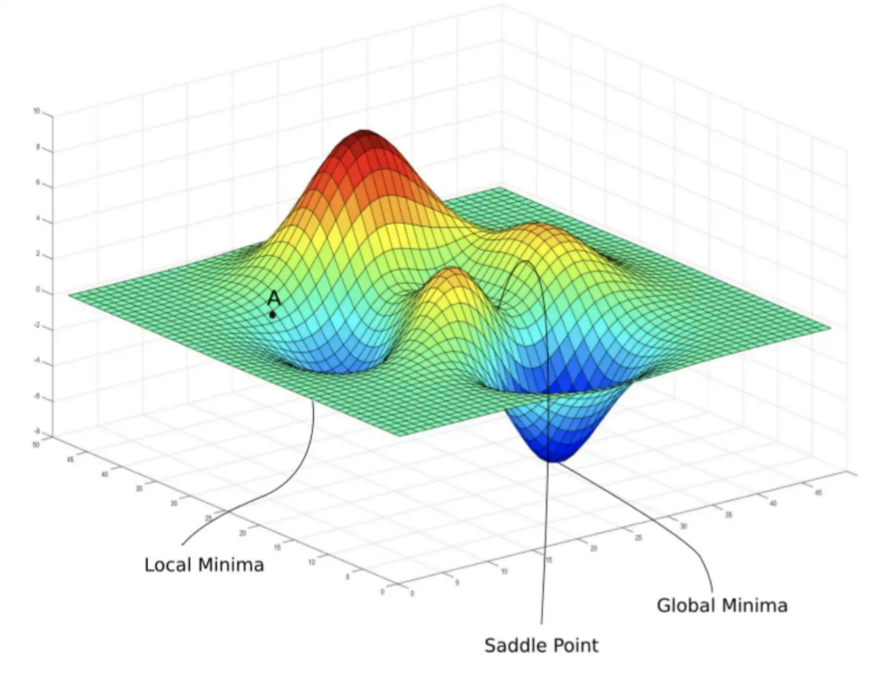
하지만 이 방법도 여러가지 문제가 있다.

  • 실제로 위 그림처럼 cost가 convex하지 않을 수 있다.
    • saddle points와 같은 점들
    • gradient 만으로는 local minimum인지 알 수 없음
  • 미분이 가능해야한다(differentiable).
    • 일부 loss function들은 미분이 불가능한 점이 존재
  • 수렴(converging)도가 매우 느림.
    • 일반 gd는 모든 데이터셋에 대해 gradient를 계산해야하는 방식

Stochastic Gradient Descent

이러한 문제를 개선하고자, 전체 데이터셋에서 일부 dataset만 sampling하여 학습에 사용하겠다는 것이 확률적 경사하강법(SGD; Stochastic Gradient Descent)이다.

sample size는 32,64,128 등으로 사용하며, 이를 mini-batch라고 부른다.

*diminishing returns: mini-batch가 작을 때는 size가 조금 커지면(32->64) 성능이 금방 좋아지지만, 이미 size가 큰 상황에서는 더 커질때(8,192->16,384) 늘어나는 연산량 대비 성능개선이 적은 편이다.

SGD를 이용한 training curve에서 왜 noise가 나타날까??

jpg
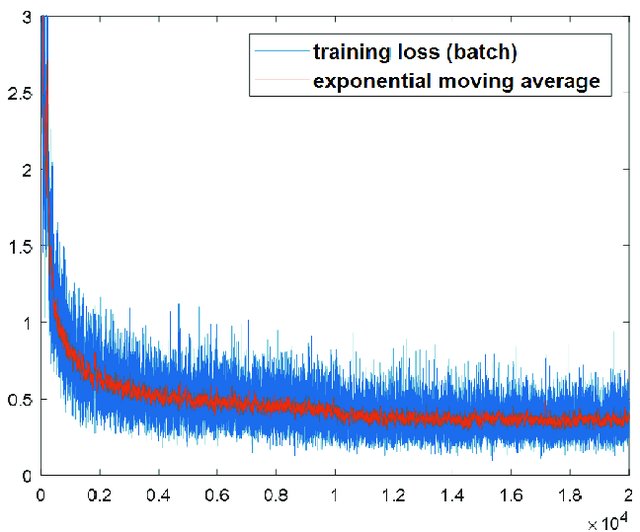
Source : Conference paper

  • 한 epoch마다 mini-batch로 쪼개서 학습시키기 때문에 (즉, 전체 데이터셋이 아니기 때문에) update된 gradient가 가끔은 증가할 수도 있는 noise가 생기는 것이다.


Reference

이 포스팅은 cs231n 수업(by Prof. Li Fei-Fei at Stanford University)과 Machine Learning for Visual Understanding (by 서울대학교 이준석 교수님) 수업을 듣고 공부하며 작성하였습니다.

https://cs231n.github.io/

http://viplab.snu.ac.kr/viplab/courses/mlvu_2021_2/index.html

https://greeksharifa.github.io/machine_learning/2021/10/24/Margin-Based-Loss/#sigmoidloss

https://say-young.tistory.com/entry/CS231n-Lecture-3-Loss-Functions

https://opentutorials.org/module/3653/22995

댓글남기기

참고