[Handson ML] 로지스틱(Logistic), 소프트맥스(Softmax) 회귀 - 모델 훈련

개요

분류 문제에서 주로 활용되는 로지스틱(logistic), 소프트맥스(softmax)에 대해 알아보자.
소프트맥스는 로지스틱과 개별적으로 알고있는 경우가 많으나, 다항 로지스틱(Multinomial Logistic)이라고도 불린다.

로지스틱(logistic) 회귀

로지스틱 회귀(Logistic Regression) 는 회귀 알고리즘이지만 분류문제에서 주로 사용된다.

추정 확률(predict_proba()와 같은)이 50%가 엄으면 해당 범주에 속한다고 예측하고, 아니면 속하지 않는다고 예측한다.

이것을 이진 분류기(Binary Classifier)라고 한다.

1. 확률 추정

로지스틱 회귀는 선형회귀모델과 같이 입력 변수의 가중치 합을 계산하고(편향도 더한다) 바로 예측값을 출력하지 않고 결과값의 로지스틱(logistic)을 출력한다.

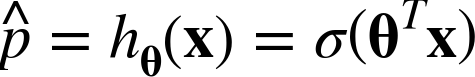
위 식은 로지스틱 회귀모델의 확률(p_hat)추정 식이다.
로지스틱은 줄여서 로짓이라고도 부르며 σ(·)로 표시하는데 0~1의 값을 출력하는 시그모이드 함수(sigmoid function) 이다.

이 함수에 대한 시기은 다음과 같다.

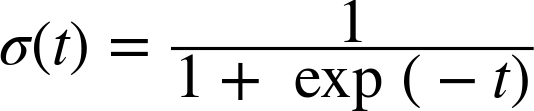
이 시그모이드 함수를 구현해서 시각적으로 표현해보자.

[-10, 10] 구간안에 100개의 t값을 시그모이드 함수에 대입한다.

import numpy as np

t = np.linspace(-10, 10, 100)
sig = 1 / (1 + np.exp(-t))

t와 시그모이드 결과값을 plotting 해보자.

plt.figure(figsize=(9, 3))
plt.plot([-10, 10], [0, 0], "k-")
plt.plot([-10, 10], [0.5, 0.5], "k:")
plt.plot([-10, 10], [1, 1], "k:")
plt.plot([0, 0], [-1.1, 1.1], "k-")
plt.plot(t, sig, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$")
plt.xlabel("t")
plt.legend(loc="upper left", fontsize=20)
plt.axis([-10, 10, -0.1, 1.1])

plt.show()

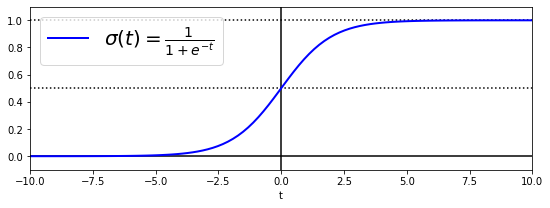
위와 같이 시그모이드 함수는 S자 형태를 띄며, 어떤 값(t)을 대입하면 0~1사이의 값을 반환하도록 해준다.

이를 이용해 양상 범주에 속할 확률을 추정하면, 이에 대한 예측 y_hat을 쉽게 구할 수 있다.

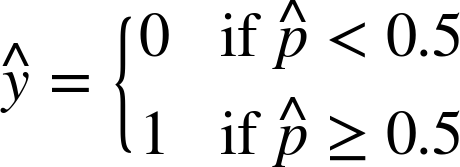
위에서 간단히 구한 결과는 t ≥ 0 이면 σ(t) ≥ 0.5이므로(반대는 반대로), 시그모이드 공식과 함께 생각하면 θ^T·x가 양수일때 1(양성 범주), 음수일 때 0(음성 범주)이라고 예측한다.

사이킷런의 LogisticRegression은 범주 레이블을 반환하는 predict()메서드와 (시그모이드 함수를 이용한)범주에 속할 확률을 반환하는 predict_proba()메서드를 가지고 있다.

2. 훈련과 비용함수

이제 로지스틱 회귀모델이 어떻게 확률을 추정하는지 알았으므로 훈련시켜보자.

훈련의 목적은 양성 샘플(y=1)에 대해서는 높은 확률, 음성 샘플(y=0)에 대해서는 낮은 확률을 추정하는 모델의 파라미터 벡터 θ를 찾는게 될 것이다.

이러한 아이디어로 하나의 훈련샘플 X에 대해 나타낸 비용함수 식이 다음과 같다.

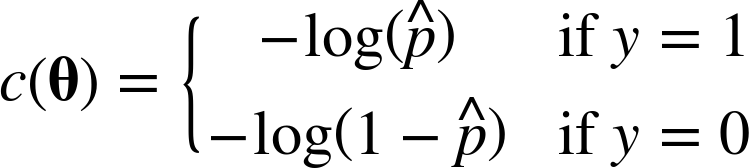
위 식을 직관적으로 이해해보면, t가 0에 가까워 질수록 -log(t)가 매우 커져서 비용이 크게 증가한다.

즉, 양성 샘플(y=1)인데 이 확률을 0에 가깝게 추정(음성이라고 추정)하면 비용함수가 매우 커진다는 의미로 이해할 수 있다.

반대로 t가 1에 가까워지면 -log(t)는 0에 가까워져 비용은 0이 된다.

전체 훈련 세트에 대한 비용함수는 모든 훈련 샘플의 비용을 평균한 것이다. 이를 로그 손실(log loss) 라고 하며 다음과 같이 쓸 수 있다.

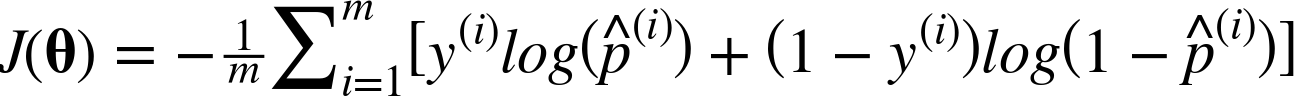
대괄호[]안을 보면 양성 범주일때 y(i)=1이 되고 1-y(i)=0이 되어 첫번째 항만 남게되고, 반대의 경우는 두번째 항만 남게되면서 결국 하나의 샘플에 대한 비용함수 C(θ)식과 같아진다.

이 비용함수는 정규방정식에서와 같이 최솟값을 계산하는 해가 존재하지 않는다.

하지만, 볼록함수이므로 경사하강법(또는 다른 최적화 알고리즘)이 전역 최솟값을 찾는 것을 보장한다.

이 비용함수의 j번째 모델 파라미터 θj에 대해 편미분하면 다음과 같다.

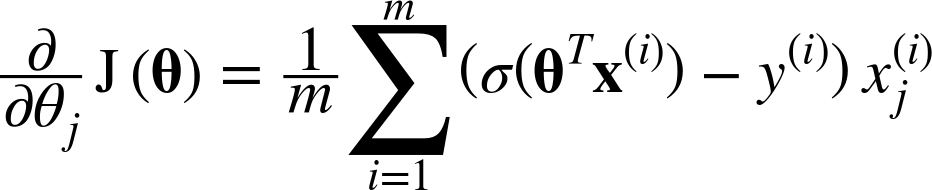
이는 배치 경사하강법에서 배웠던 비용함수MSE의 편도함수와 매우 비슷한 형태이다.

각 샘플에 대해 예측 오차를 계산하고, j번째 변수값을 곱하고, 모든 훈련 샘플 수로 나누어 평균을 낸다.

마찬가지로 모든 편도함수를 포함한 그래디언트 벡터를 만들면 배치 경사하강법 알고리즘을 사용할 수 있다.

3. 결정 경계

이제 로지스틱 모델을 훈련시켜보자.
데이터셋은 붓꽃(iris) 데이터를 한다. 이는 3개의 품종(Iris-Setosa, Iris-Versicolor, Iris-Vierginica)에 속하는 150개의 꽃잎(petal)과 꽃받침(sepal)의 너비와 길이를 담고 있다.

정리하면 샘플 수는 150개, 변수는 4개, 범주는 3개로 이루어진 데이터이다.

그러면 이제 꽃잎의 너비를 기반으로 Iris-Versinica종을 감지하는 이진분류기를 만들어 보자.

# 데이터 로드
from sklearn import datasets

iris = datasets.load_iris()
list(iris.keys())

['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']

X = iris["data"][:,3:]    # 꽃잎의 너비 변수만 사용
y = (iris["target"]==2).astype("int")  # iris-Versinica면 1, 아니면 0

# 로지스틱 회귀모델 훈련
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(solver='liblinear')
log_reg.fit(X,y)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='warn', n_jobs=None, penalty='l2',
                   random_state=None, solver='liblinear', tol=0.0001, verbose=0,
                   warm_start=False)

그러면 이제 꽃잎의 너비가 0~3cm인 꽃에 대해 모델의 추정확률을 계산해보자.

import matplotlib.pyplot as plt

X_new = np.linspace(0,3,1000).reshape(-1,1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:,1], "g-", label = "Iris-Virginica")
plt.plot(X_new, y_proba[:,0], "b--", label = "not Iris-Virginica")
plt.legend()
plt.show()

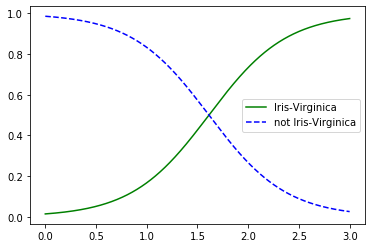
좀더 보기좋게 그려보자.

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]

plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], "bs")  # 음성범주 pointing
plt.plot(X[y==1], y[y==1], "g^")  # 양성범주 pointing

# 결정경계 표시
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)

# 추정확률 plotting
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")

plt.text(decision_boundary+0.02, 0.15, "Decision  boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])

plt.show()

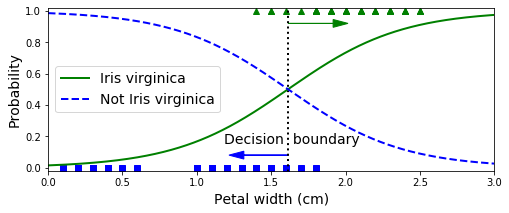
그래프를 보면 Iris-Verginica(y=1)는 꽃잎 너비가 1.4~2.5cm 사이에 분포(초록 삼각형)한다.

그리고 Iris-Verginica가 아닌 꽃들은 일반적으로 꽃잎 너비가 더 작아 1.8cm보다 작게 분포한다. 그래서 약간 중첩되는 구간이 존재한다.

decision_boundary

array([1.61561562])

양쪽의 확률이 50%가 되는 1.6cm 근방에서 결정경계(decision boundary)가 만들어지고, 분류기는 1.6cm보다 크면 Iris-Verginica로 분류하고 작으면 아니라고 예측할 것이다.

log_reg.predict([[1.7], [1.5]])

array([1, 0])

확인해보니 정말 그렇다.!

이번에는 꽃잎 너비와 꽃잎 길이 2개의 변수를 이용해 훈련시켜보자.

from sklearn.linear_model import LogisticRegression

X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.int)

log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)

x0, x1 = np.meshgrid(
        np.linspace(2.9, 7, 500).reshape(-1, 1),
        np.linspace(0.8, 2.7, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]

y_proba = log_reg.predict_proba(X_new)

• 사이킷런의 LogisticRegression모델의 규제강도를 조절하는 하이퍼파라미터는 alpha가 아니라 그 역수에 해당하는 C이다.
• C가 높을수록 모델의 규제가 줄어든다.

plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs")
plt.plot(X[y==1, 0], X[y==1, 1], "g^")

zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)


left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]

plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])

plt.show()

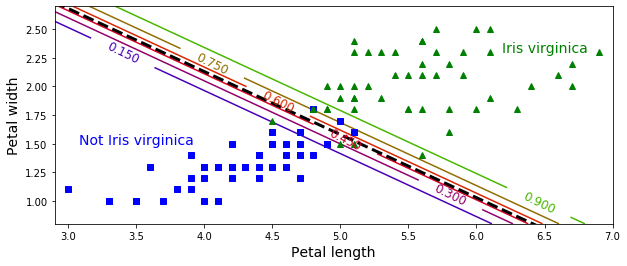
위 그래프의 점선은 모델이 50% 확률을 추정하는 지점으로, 이 모델의 결정경계이다.
(이 경계는 θ0 + θ1x1 + θ2x2 = 0을 만족하는 (x1,x2)의 집합으로 선형경계 임을 주목하자)

이 (x1,x2)조합에 따라 Iris-Verginica에 속할 확률을 15%부터 90%까지 나타내고 있다.

다른 선형 모델처럼 로지스틱 회귀 모델도 ℓ1,ℓ2 페널티를 사용하여 규제할 수 있고, 사이킷런은 ℓ2 페널티를 기본으로 한다.

4. 소프트맥스 회귀

로지스틱 회귀모델은 여러 개의 이진 분류기를 훈련시켜 연결하지 않고, 직접 다중 범주를 지원하도록 일반화될 수 있다.

이를 소프트맥스 회귀(Softmax Regression) 또는 다항 로지스틱 회귀(Multinomial Logistic Regression) 라고 한다.

개념은 간단한데, 샘플 X가 주어지면 소프트맥스 회귀 모델이 각 클래스 k에 대한 점수 s_k(x)를 계산하고, 그 점수에 소프트맥스 함수(또는 정규화된 지수함수)를 적용하여 각 범주별 속할 확률을 추정한다.

범주 k에 대한 점수 s_k(x)를 계산하는 식은 다음과 같다.

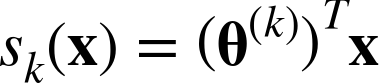
위 식처럼 각 범주들은 자신만의 파라미터 벡터 θ(k)를 가지고 있고, 파라미터 행렬 Θ에 행으로 저장된다.

이렇게 샘플 x에 대해 각 범주들의 점수가 계산되면 소프트맥스 함수를 통과시켜 범주k에 속할 확률 p_hat_k를 추정한다(이 함수는 각 점수에 지수함수를 적용한 후 정규화를 한다).

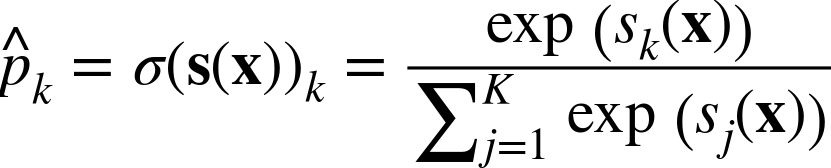
• k : 범주의 수
• s(x) : 샘플 x에 대한 각 범주의 점수를 담고 있는 벡터
• σ(s(x))k : 이 샘플이 범주 k에 속할 확률

소프트맥스 회귀 분류기도 로지스틱 회귀와 마찬가지로 추정확률이 가장 높은 범주를 선택한다.

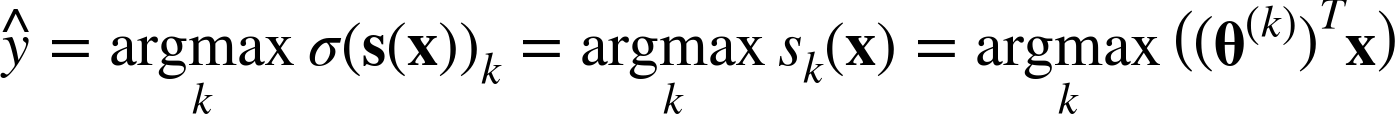
• argmax연산은 함수를 최대화하는 변수의 값을 반환한다(numpy에도 비슷한 함수가 있는데 array에서 최댓값을 가지는 원소의 index를 반환).
• 위 함수에서는 추정확률 σ(s(x))k가 최대인 k값을 반환

소프트맥스 회귀 분류기는 한 번에 하나의 범주만 예측한다(다중 범주이지만, 다중출력은 아니다).
따라서 붓꽃처럼 상호 배타적인 범주에 대해서 사용이 가능하다(하나의 사진에 여러 사람의 얼굴을 인식하는 경우는 불가능하다).

그렇다면 이제 훈련을 시켜보자.

훈련의 목적은 모델이 타깃 범주에 대해서는 높은 확률(다른 범주면 낮은 확률)을 추정하도록 하는 것이다.

다음의 크로스 엔트로피(cross entropy) 비용함수를 최소화 하는 것은 타깃 범주에 대해 낮은 확률을 예측하는 모델을 억제하므로 목적과 부합하다.

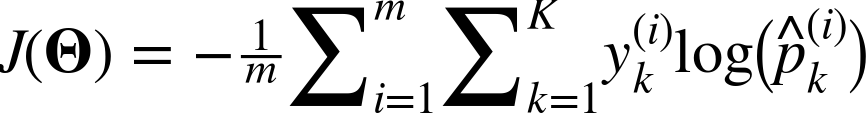
• i번째 샘플에 대한 타깃 범주가 k일때, y(i)k가 1이고, 그 외에는 0이다.

크로스 엔트로피는 추정된 범주의 확률이 타깃 범주에 얼마나 잘 맞는지 측정하는 용도로 종종 사용된다.

이해를 돕기위해 이진분류라고 가정하면(K=2), 이 비용함수는 로지스틱 회귀의 비용함수와 같아질 것이다.

이 비용함수의 θ(k)에 대한 그래디언트 벡터는 다음과 같다.

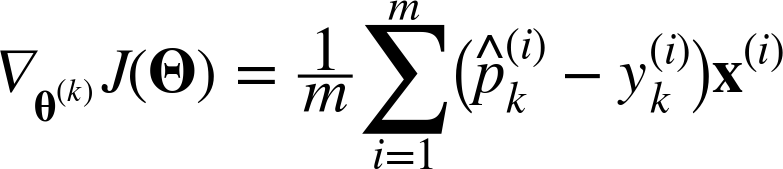
이제 각 범주에 대한 그래디언트 벡터를 계산할 수 있으므로 비용함수를 최소화하기 위한 파라미터 행렬Θ를 찾기 위해 경사하강법을 사용할 수 있을 것이다.

사이킷런의 LogisticRegression은 범주가 2이상이면 일대다(OvA) 전략을 사용한다(분류 포스팅 참고).

하지만 multi_class='multinomial'옵션을 주면 소프트맥스 회귀를 사용할 수 있다.
또한 solver='lbfgs'옵션을 주어 소프트맥스 회귀를 지원하도록 알고리즘을 지정해야 한다.

그리고 하이퍼파라미터 C를 사용하여 조절할 수 있는 ℓ2규제가 적용된다.

다음 코드를 보자.

X = iris["data"][:, (2, 3)]  # 꽃잎 길이와 너비 변수
y = iris["target"]           # 3개의 범주 그대로 사용

softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)

LogisticRegression(C=10, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='multinomial', n_jobs=None, penalty='l2',
                   random_state=42, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)

이제 꽃잎 길이가 5cm, 너비가 2cm인 붓꽃을 발견했다고 가정하고 품종을 분류하도록 분류기에 넣어보자.

softmax_reg.predict([[5,2]])

array([2])

softmax_reg.predict_proba([[5,2]])

array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])

약 94%의 확률로 Iris-Verginica(y=2)라고 분류하는 것을 알 수 있다.

이렇게 훈련시킨 소프트맥스 분류기의 결정경계를 시각화 해보자.

# 새로운 샘플 생성
x0, x1 = np.meshgrid(
        np.linspace(0, 8, 500).reshape(-1, 1),
        np.linspace(0, 3.5, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]


y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")

from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])

plt.show()

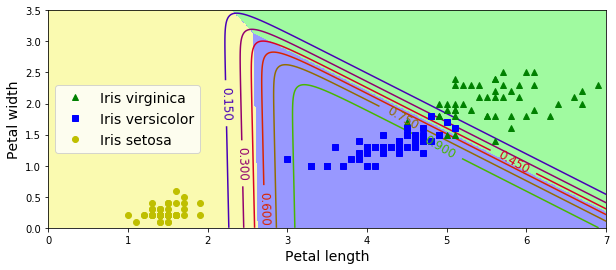
3개의 범주지만, 범주와 범주 사이의 결정경계(배경색)가 모두 선형임을 알 수 있다.

이 모델은 이진분류와 달리 0.5의 경계가 아니라 범주에 속할 확률이 0.5 이하 이더라도 분류한다는 점을 유의하자(범주가 2개보다 많으므로).
예를들어 모든 결정경계가 만나는 지점은 동일하게 33.3%의 추정확률을 갖는다.

Reference

도서 [Hands-0n Machine Learning with Scikit-Learn & Tensorflow] 를 공부하며 작성하였습니다.