[ML] 은닉 마르코프 모델 (Hidden Markov Model, HMM)
업데이트:
개요
이번 포스팅은 sequential data(ex 날씨, 주식, 자연어, ..)를 모델링하는데 이점을 지니고 있는 은닉 마르코프 모델(Hidden Markov Model, HMM)에 대한 글이다. HMM은 마르코프 체인(Markov chain)을 확장한 모델이라고 볼 수 있다.
마르코프 연쇄(Markov chain)란?
마르코프 연쇄(Markov chain)는 마르코프 성질(Markov Property)을 가진 이산확률과정(discrete-time stochastic process)를 의미한다.
- 이산확률과정(discrete-time stochastic process) : 시간이 연속적으로 변하지 않고 이산적으로 변하며(현재상태 -> 다음상태), 이에 따라 특정 상태가 발생할 확률이 변화하는 과정
- 마르코프 성질 : 미래의 상태($o_t$)는 오직 현재의 상태($o_{t-1}$) 혹은 더 이전의 일정기간($o_{t-1},o_{t-2},…$)에만 영향을 받는다고 가정. 즉, 미래의 어떤 상태를 예측하기 위해 과거의 긴 이력을 필요로 하지 않는 성질(memoryless)
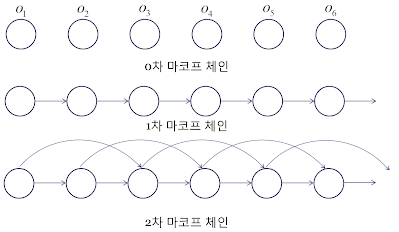
바로 이전상태(r=1) 혹은 더 이전 상태(r=2)까지 고려한다고 했을 때, 아래 그림과 같이 r차 Markov chain으로 나타낼 수 있다.
즉 바로 이전상태만 고려하는 확률식은 아래와 같이 나타낼 수 있다.
\[P(o_{t}|o_{1},...,o_{t-1}) = P(o_{t}|o_{t-1})\]이러한 아이디어는 생각보다 우리의 현실 세계를 잘 반영한다. 바로 앞에 닥친 우리의 미래가 과거의 긴 역사를 바탕으로 하기보다 바로 최근의 과거에 의존하는 경우가 많기 때문이다.
예를들어 우리가 매일 같이 이동하는 패턴에서도 날씨에 따라, 교통 상황에 따라, 기분에 따라 등등 그때 그때 즉각적으로 반응하기 마련이다.
은닉 마르코프 모델(Hidden Markov Model)
은닉 마르코프 모델은 위와 같은 확률모델에 숨겨진 상태 (Hidden state) 라는 개념이 추가된다.
내가 적용했던 문제로 예를 들면 우리가 가진 정보는 사람들의 이동 기록 밖에 없지만, 단순히 다음번의 이동이 아니라 각 이동에 어떤 목적 (출근, 귀가, 여가 등) 이 숨겨져 있는지를 알고 싶었다.
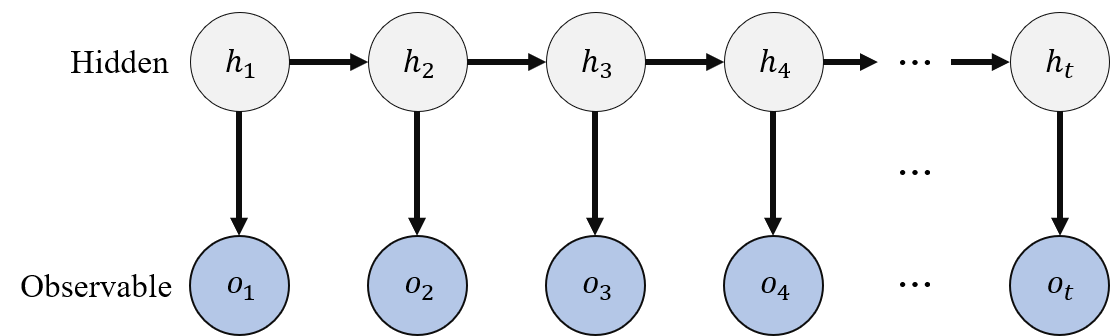
아래 그림처럼 우리가 갖고 있는 정보는 $o_{t}$ 뿐이며, 이들의 sequence를 통해 숨겨진 상태인 $h_{t}$의 sequence를 추론하고 싶은 것이다.

HMM의 파라미터
HMM은 앞서 말했듯이 관측치(Observable state)와 은닉 상태(Hidden state)로 구성되며 우리가 알고 싶은 state의 수는 미리 결정되어야 한다.
가능한 hidden state의 집합을 $S={S_{1},S_{2},S_{3},…,S_{N}}$라고 했을 때, HMM의 주요 파라미터는 3가지가 있다.
1. Initial Probability (초기 확률)
\[\pi=\{\pi_{i}\} = \{P(h_{1}=S_{i})\}, 1≤i≤N\]초기확률은 가장 처음 state $h_{1}$이 $S_{i}$에서 시작할 확률을 의미한다.
2. Transition Probability (전이 확률)
\[A=\{a_{ij}\} = \{P(h_{t}=S_{j}|h_{t-1}=S_{i})\}, 1≤i,j≤N\]Hidden state 간의 전이확률은 NxN개의 정사각형 행렬로 아래와 같이 도식화 된다. 여기서 현재 상태 $h_{t}$는 바로 이전 상태 $h_{t-1}$에만 의존한다. 따라서 N개의 state에 대해 t-1번째 i state에서 t번째 j state로 전이되는 행렬을 구성한다.
3. Emission Probability (방출 확률)
\[B=\{b_{i}(k)\} = \{P(o_{t}=k|h_{t}=S_{i})\}, 1≤i≤N, 1≤k≤M\]특정 hidden state $h_{t}$로 부터 observation이 관측될 확률을 의미한다. 여기서 K는 관측치의 가능한 집합이 M개 있을 때의 변수이며, 방축확률은 NxM 행렬을 구성한다.
최종적으로 HMM의 파라미터 아래와 같다.
\[\lambda = \{\pi, A, B\}\]HMM 적용
HMM이 풀수 있는 문제는 크게 3가지가 있다.
- Learning parameter
- likelihood computation
- Decoding
Learning : Baum-Welch algorithm
\[\hat{\lambda} = argmax_{\lambda}\prod_{t}^{T} P(o_{t}|\lambda)\]HMM의 파라미터는 관측치의 집합 $O={o_{1},o_{2},o_{3},…,_{k}}$으로 부터 우도함수(likelihood)를 최대화하는 방향으로 추정한다.
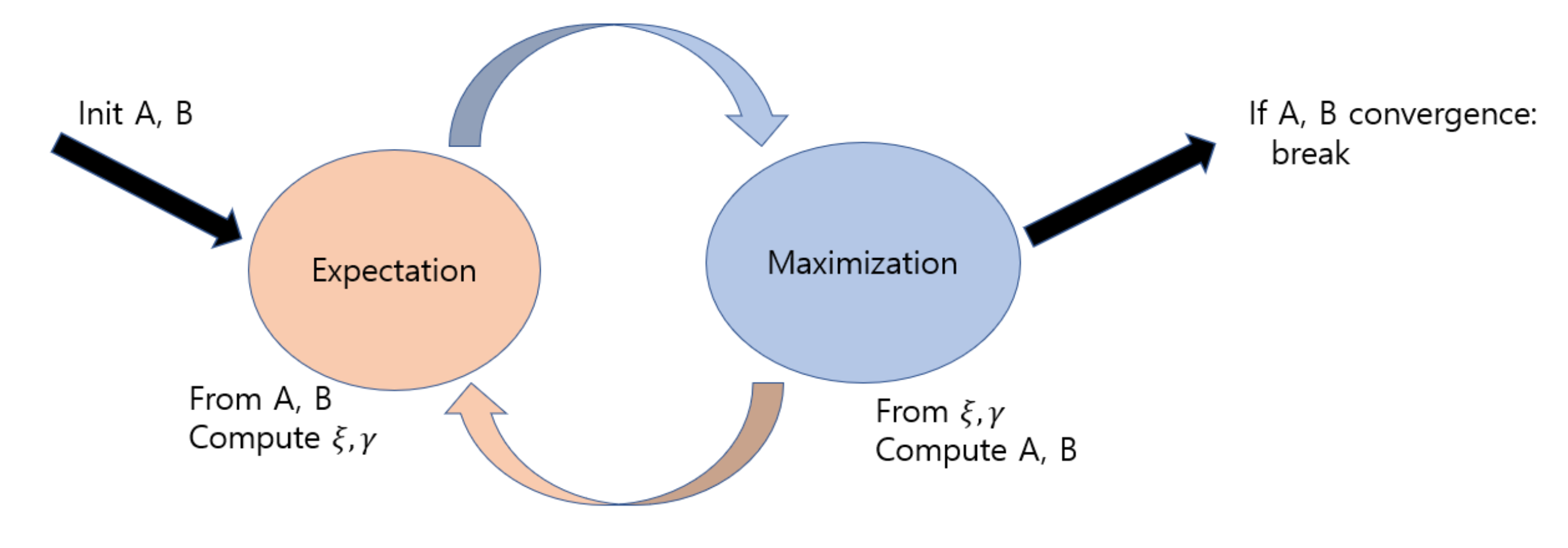
Baum-Welch 알고리즘은 Expectation-Maximization(EM) 알고리즘의 일종으로, 아래와 같이 두 과정을 반복하며 최적의 $\lambda$를 찾아간다.
- E-step : A,B가 고정된 상태에서 $\xi$, $\gamma$ 계산
- M-step : $\xi$, $\gamma$가 고정된 상태에서 A,B를 업데이트
$P(O|\lambda^{new})>P(O|\lambda)$ 인 최적 추정값 도출할 때 까지 1과 2를 반복한다.
Notation : A(전이확률), B(방출확률), $\xi$(전이 기대값) ,$\gamma$(state의 기대값)
pesudo code는 아래와 같다.
likelihood computation : Forward algorithm
HMM의 파라미터 $\lambda$와 관측치의 sequence $O$가 주어졌을 때, 이 $O$가 관측될 확률을 계산하는 것이다. 즉 우도함수(likelihood)를 구하는 것이다.
먼저 단순히 계산을 해보자.
1번 관측치가 나타날 확률 \(P(o_{1})=\displaystyle\sum_{i_{1}} p(S_{i_{1}})p(o_1|S_{i_1})\)
1,2번이 연속으로 나타날 확률
\(P(o_{1},o_{2})=\displaystyle\sum_{i_{1}} p(S_{i_{1}})p(o_1|S_{i_1})\displaystyle\sum_{i_{2}} p(S_{i_{2}}|S_{i_{1}})p(o_2|S_{i_2})\)
T개 sequence가 연속으로 나타날 확률
\(P(O)=\displaystyle\sum_{i_{1}}\displaystyle\sum_{i_{2}}...\displaystyle\sum_{i_{T}}p(S_{i_{1}})p(o_1|S_{i_1})p(S_{i_{2}}|S_{i_{1}})p(o_2|S_{i_2})...p(S_{i_T}|S_{i_{T-1}})p(o_T|S_{i_T})\)
이와 같이 hidden state가 N개이고 관측치 sequence의 길이가 T라면, $N^T$개의 경우의 수가 발생하며 계산적 비효율성이 발생하게 된다.
따라서 이를 위해 dynamic programming 기반의 Forward algorithm을 사용하게 된다. 이는 중복되는 계산을 컴퓨터에 저장해 두었다가 재사용하는 것이 핵심이다. 예를들어 위에서 1,2의 확률에는 1의 확률이 포함되어 있으므로 갖고있다가 바로 쓰자는 얘기다.
pesudo code는 아래와 같다.

source
Decoding : Viterbi algorithm
Decoding 문제는 모델 $\lambda$와 관측치(observation) sequence가 주어졌을때, hidden state의 sequence $S$를 찾고 싶은 것이다. HMM이 풀고자하는 궁극적인 문제라고 할 수 있다. 이를 위해서는 Viterbi algorithm이 사용된다. 앞의 Forward algorithm과 계산방식은 유사하다.
pesudo code는 아래와 같다.

source
Python 라이브러리 : hmmlearn
HMM을 제공하는 python 라이브러리는 hmmlearn가 있다. 원래는 scikit-learn 내에서 제공되고 있었으나, 얼마전에 분리되어 독립적으로 관리되고 있는 것 같다.
공식 docs과 hmmlearn github가 있고 비교적 자주 업데이트를 해주는 것 같다. 그러나 실제로 적용된 알고리즘들의 수식을 볼수가 없어서, 확인하려면 일일이 소스코드를 까봐야하는 불편함이 있다….
다른 사람들이 만들어 놓은 github 소스도 많이 있다.
최근에 진행했던 연구에서 대중교통 스마트 카드 tagging 데이터에 hmm을 적용했었는데, 코드 설명을 위해 간략하게 활용하려고 한다.
from hmmlearn.hmm import GaussianHMM,GMMHMM
import pandas as pd
import numpy as np
X = pd.read_csv("ex_dt.txt", encoding='cp949')
X.head(10)
데이터는 한 사람이 특정 장소에 도착 tag를 한 후, 다음 이동을 위해 tag하기 까지의 기록으로 정제되어 있는 데이터 샘플이다.
예를 들면, 아래와 같이 id0이라는 사람은 하루의 첫 장소에 16시 쯤(start time) 도착해서 15시간(duration) 정도 머물렀고, 다음장소로는 오전 8시쯤 도착해서 6.9시간 정도 머물렀다고 해석하면 된다.
| id | start_time | duration | |
|---|---|---|---|
| 0 | 0 | 16.183333 | 15.843333 |
| 1 | 0 | 8.516667 | 6.946111 |
| 2 | 0 | 15.966667 | 19.434444 |
| 3 | 1 | 18.316667 | 14.366944 |
| 4 | 1 | 9.083333 | 7.305278 |
| 5 | 1 | 16.750000 | 1.521111 |
| 6 | 1 | 18.566667 | 13.775278 |
| 7 | 2 | 21.700000 | 11.204444 |
| 8 | 2 | 9.583333 | 11.570278 |
| 9 | 2 | 21.800000 | 11.159444 |
hmmlearn.hmm에는 GaussianHMM, GMMHMM, Multinomial HMM을 제공한다.
이들은 input data가 discrete인지, continuous인지에 따라 Emission probability 계산 시 필요한 모델이 달라지기 때문에 알고 사용해야한다. 자세한 내용은 공식 홈페이지를 참고하면 될 것 같다.
- Multinomial HMM : input이 discrete 함
- GaussianHMM : input이 continuous 함
- GMMHMM : 여러개의 gaussian 모델로 확장된 모델
여기서는 GaussianHMM을 썼다.
중요한 파라미터는 n_components로 hidden state의 개수를 지정하는 값이다. 클러스터링에서 k값을 지정하는 것과 유사하다.
model = GaussianHMM(n_components=4, verbose=True, n_iter=100, random_state= 108).fit(X)
1 -1152.1125 +nan
2 -1044.2909 +107.8216
3 -992.7844 +51.5065
4 -974.6446 +18.1398
5 -959.1834 +15.4613
6 -874.2685 +84.9149
7 -838.1007 +36.1678
8 -838.0098 +0.0909
9 -837.9890 +0.0207
10 -837.9857 +0.0033
그런데 여기서 앞서 얘기한 데이터는 하나로 이어진 sequence가 아니라 한 사람마다 sequence를 가지고 있는 multi sequence 데이터이므로, 다른 방법이 필요하다.
다행히 이런 경우도 라이브러리에서 제공을 해주고 있다. 각 sequence의 길이를 카운트해서 length인자를 추가해주면 된다.
lengths = X.groupby('id', sort=False).size().tolist()
model = GaussianHMM(n_components=4, verbose=True, n_iter=100, random_state= 108).fit(X,lengths)
데이터가 작아서 금방 fitting이 됐다. predict할 때도 length는 필요하고, 요약해보면 3번 state가 35개로 가장 많고 나머지도 적절하게 state가 생성되었음을 알 수 있다.
X["hidden_state"] = model.predict(X,lengths)
X["hidden_state"].value_counts()
3 35
0 28
1 19
2 18
Name: hidden_state, dtype: int64
여기서 중요한 점은 HMM의 파라미터를 통해 우리는 이 결과가 합리적인지 해석적으로 접근할 수 있는 장점이 있다.
먼저 transiton probability는 4개의 state들 간의 전환확률을 나타낸다고 했다. 이것을 이동의 목적들과 비교했을 때 합리적인지 해석할 수 있을 것이다. initial prob도 마찬가지.
# Print trained parameters and plot
print(">> Transition matrix")
print(np.round(model.transmat_, 2))
print()
print(">> Initial Probability")
print(np.round(model.startprob_, 2))
print()
>> Transition matrix
[[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0.77 0. 0.23 0. ]
[0. 0.99 0. 0.01]]
>> Initial Probability
[0.42 0. 0. 0.58]
그리고 각 state들에 포함된 이동의 기록들이 어떤 통계치를 가지는지 살펴보면, 대략 무엇을 위한 이동이였는지 짐작할 수 있을 거라 생각한다.
print(">> Means and vars of each hidden state")
for i in range(model.n_components):
print("{0}th hidden state".format(i))
print("mean = ", np.round(model.means_[i],2))
print("var = ", np.round(np.diag(model.covars_[i]),2))
print()
>> Means and vars of each hidden state
0th hidden state
mean = [21.4 9.37 10.2 3.75]
var = [33.69 3.22 9.37 3.44]
1th hidden state
mean = [ 5.5 20.87 12.78 3. ]
var = [11.92 5.14 8.63 0. ]
2th hidden state
mean = [ 5.94 11.21 7.38 4. ]
var = [12.81 11.72 12.71 0. ]
3th hidden state
mean = [21.11 19.86 12.36 0.73]
var = [30.2 7.61 26.4 0.74]
자세한 내용은 생략하고, hmmlearn의 활용 방법에 초점을 맞추었다.
Hidden markov model은 비지도 학습(unsupervised learning)방법의 하나라고 볼 수 있을 것이다. 처음에 이해하기가 굉장히 어려웠다. sequence가 존재하는 데이터를 클러스터링 하기에 유용하고, 추정된 파라미터를 통해 해석적으로 접근할 수 있는 장점이 있는 것 같다.
Reference
https://www.youtube.com/watch?v=HB9Nb0odPRs&t=2966s
https://ratsgo.github.io/machine%20learning/2017/03/18/HMMs/
https://untitledtblog.tistory.com/97
https://sites.google.com/site/machlearnwiki/RBM/markov-chain
https://ratsgo.github.io/speechbook/docs/am/baumwelch




댓글남기기