[cs231n] Recurrent Neural Networks - RNN, LSTM
업데이트:
개요

지금까지는 image dataset을 기반으로 classify하는 문제에 대해 다뤘었다.
이번 포스팅에서는 시간 차원의 순서가 의미를 가지는 sequential한 dataset을 모델링하는데 유용한 Recurrent Neural Networks에 대해 알아보자.
Recurrent Neural Networks
background
아래 그림은 지금까지 주로 다룬 image classification task에서의 Vanilla Neural network와 sequence를 반영하고 있는 Recurrent Neural Network의 유형들을 보여주고 있다.
기존 Neural network는 one-to-one 구조로 1장의 image로부터 학습을 통해 1개의 class를 예측하는 task였지만, sequence를 반영해야 하는 다양한 task들이 존재한다.
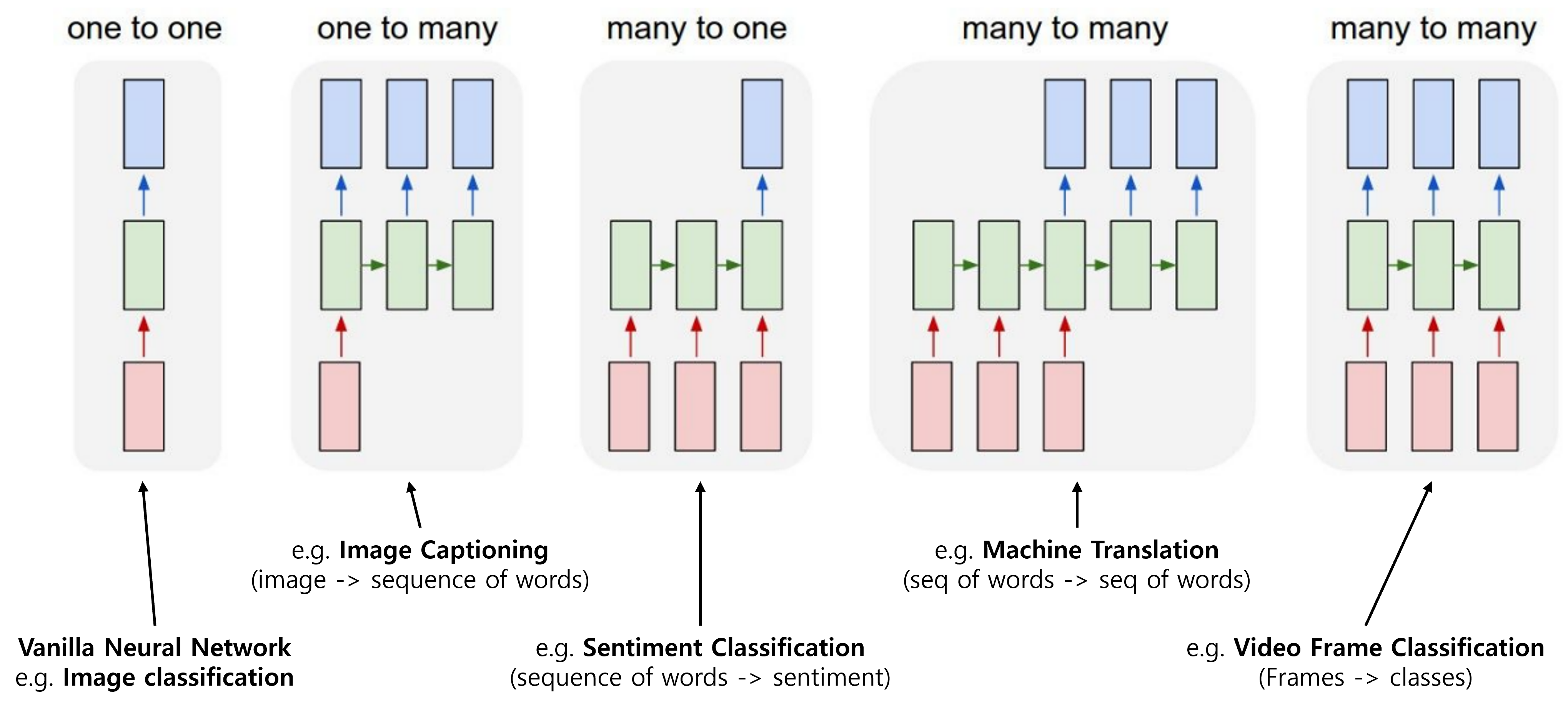
- one-to-many: Image Captioning
- 하나의 input으로 부터 여러개의 sequence output을 생성
- ex) 한 장의 이미지로 부터 해당 이미지를 설명하는 캡션(문장)을 만들어 내는 문제
- many-to-one: Sentiment Classification(감성분석)
- 여러 개의 sequence input을 통해 하나의 output을 생성
- ex) 감성분석: 단어들로 이루어진 문장으로 부터 감성(sentiment)을 분석하는 문제
- many-to-many(variable output): Machine translation
- 여러 개의 sequence input을 통해 여러 개의 sequence output을 생성
- ex) 번역: 한국어 문장으로부터 영어 문장으로 번역하는 문제
- ex) video captioning: 영상에 자막을 생성하는 문제
- many-to-many(same output): Video Frame classification
- 여러 개 sequence의 input을 통해 각 sequence에 해당하는 output을 예측
- ex) video의 각 frame 단위로 classification을 하는 문제
크게 4가지 유형의 sequence를 다루기 위해 고안된 신경망이 Recurrent Neural Networks이다.
one-to-one으로 수행했던 image classification과 같은 Non-sequential processing에 대해서 RNN을 적용할 수도 있다.
예를 들어, MNIST와 같은 손글씨 숫자 이미지 분류를 위해 단순히 CNN과 같은 모델을 사용할 수도 있지만, 사람이 숫자를 쓰는 순서가 있기 떄문에 image를 순차적으로 살펴보는 것이 도움이 될 수도 있다.
또한 이러한 특성은 classification 뿐 아니라 image 생성을 위한 generative model에도 쓰일 수 있다.
Structure
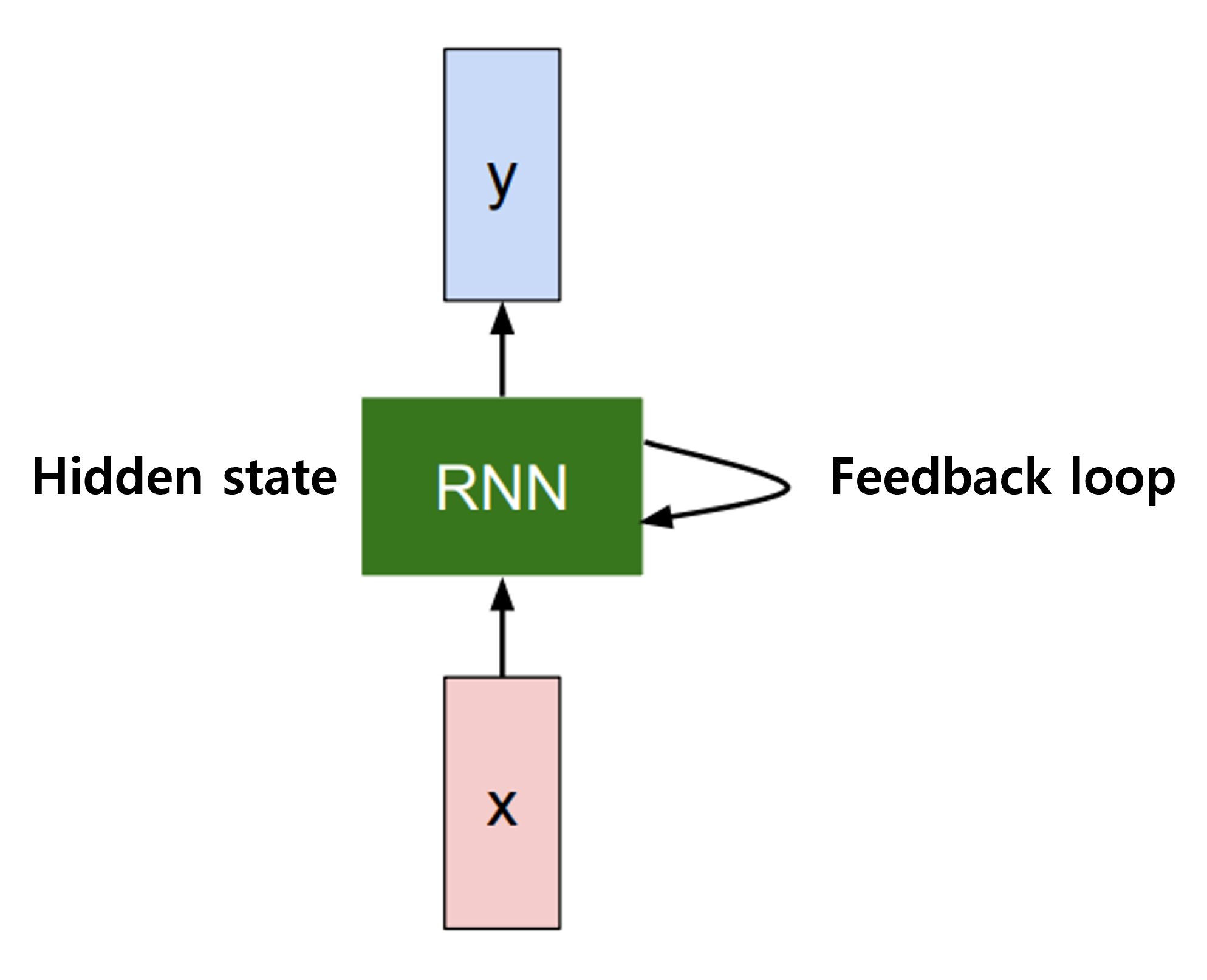
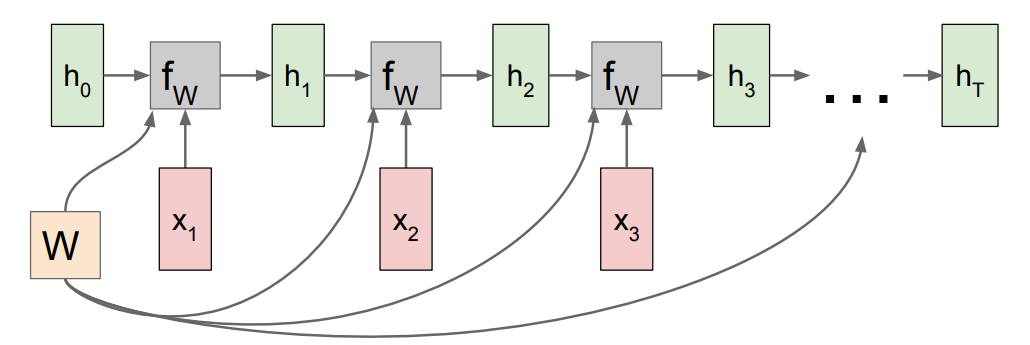
RNN은 아래 그림과 같이 feedback loop를 통해 hidden state을 지속적으로 업데이트하는 방식으로 학습한다.
즉, 기존 방식처럼 input에 대해서만 weight을 결정하는게 아니라, 이전의 hidden state도 함께 고려한다. 이렇게 해서 sequential data를 모델링 한다.
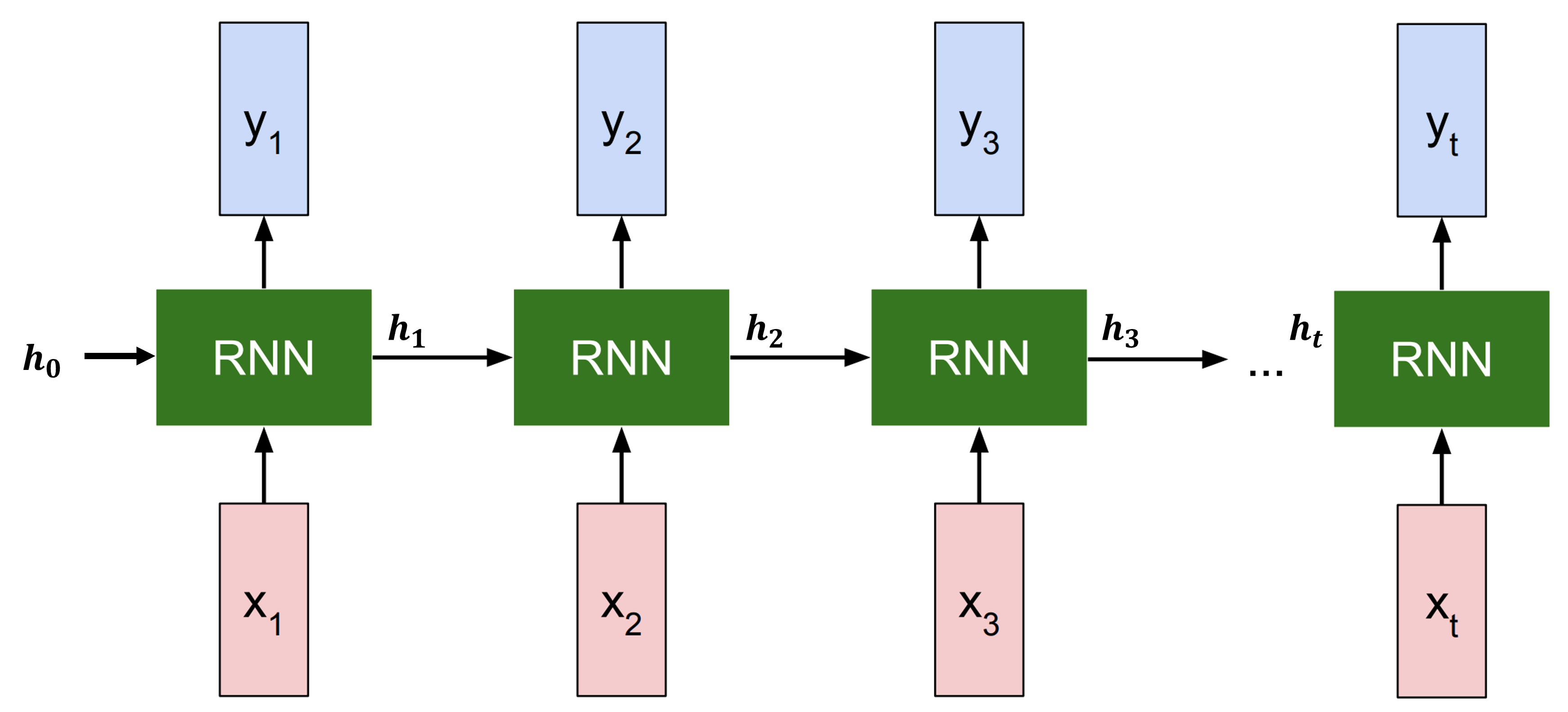
좀 더 이해하기 쉽게 sequence를 펼쳐서 forward pass를 나타내면 아래 그림과 같다.
input $x_i$가 들어올때마다 hidden state은 $h_{i-1}$에서 $h_i$로 업데이트 되며, 내부적인 계산에 따라 $y_i$가 출력된다.
그리고 처음에는 이전 hidden state이 없으므로, 초기값인 $h_0$가 주어진다.
hidden state을 업데이트하는 과정은 아래 수식으로 표기되며, 우리가 학습해야할 parameter는 $W$이다.
즉, input sequence vector ${ x_1,x_2,x_3,…,x_t }$ 가 주어졌을 때, t시점의 hidden state $h_t$는 이전 state인 $h_{t-1}$과 t시점의 input인 $x_t$에 대해 $f_W$을 적용하여 업데이트 된다.
중요한 점은 parameter $W$는 바뀌지 않고 처음부터 마지막 step까지 같은 값을 사용한다는 것이다(sequence를 반영하기 위한 중요한 사항이다).
구체적으로 simple RNN의 수식은 아래와 같이 표기된다.
학습해야할 parameter는 $W_{hh}, W_{xh}, W_{hy}$가 되며, non-linearity를 넣어주기 위해 $tanh$를 씌워준다.
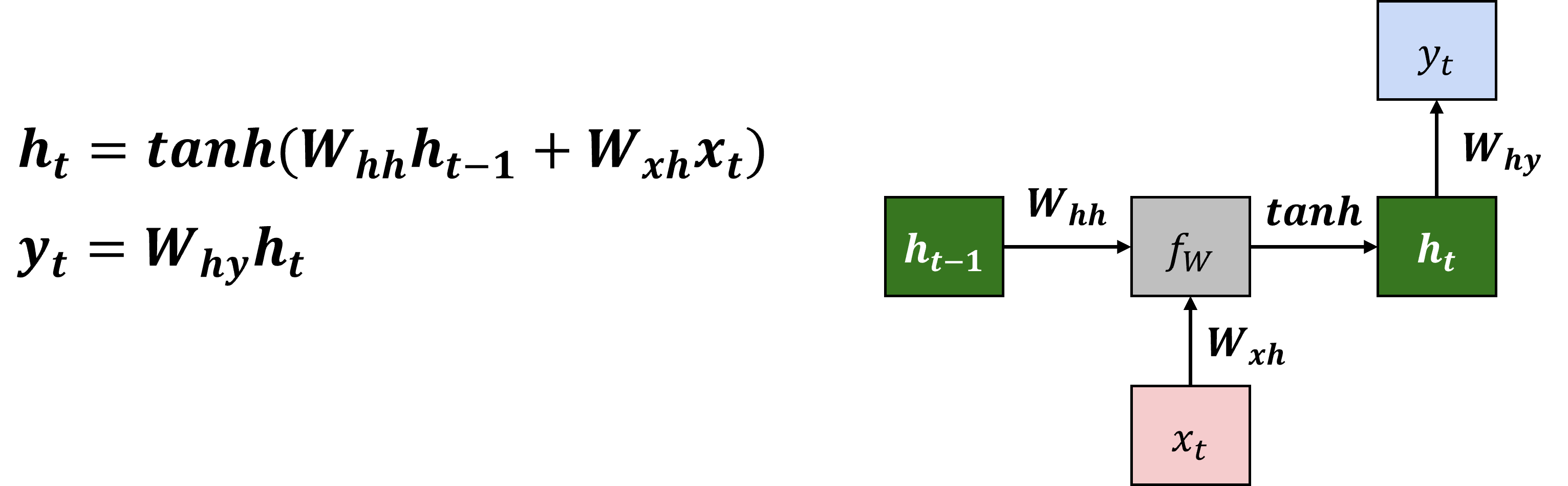
아래 그림과 같이 매 time-step마다 hidden state과 input값들은 바뀌지만, paremeter $W$ 들은 항상 같은 값을 이용하는 것을 볼 수 있다.
이제 RNN이 어떻게 학습되는지 알아보자.
지금까지 배운 neural network의 training은 아래와 같이 진행되었다.
- forward pass를 통해 $y_hat$을 출력
- ground truth인 $y$값과 비교하여 loss를 계산
- loss를 기반으로 gradient 계산(backpropagation)
- gradient를 기반으로 weight optimization
RNN도 크게 다르지 않지만, 앞서 언급했었던 구조(one-to-many 등)에 따라 동작방식이 달라지게 된다.
먼저 아래 그림은 many-to-many(same output)인 경우이다.
이때 loss는 각 step에서의 ground truth와 비교하여 계산되며, 그때마다 backpropagation이 진행된다.
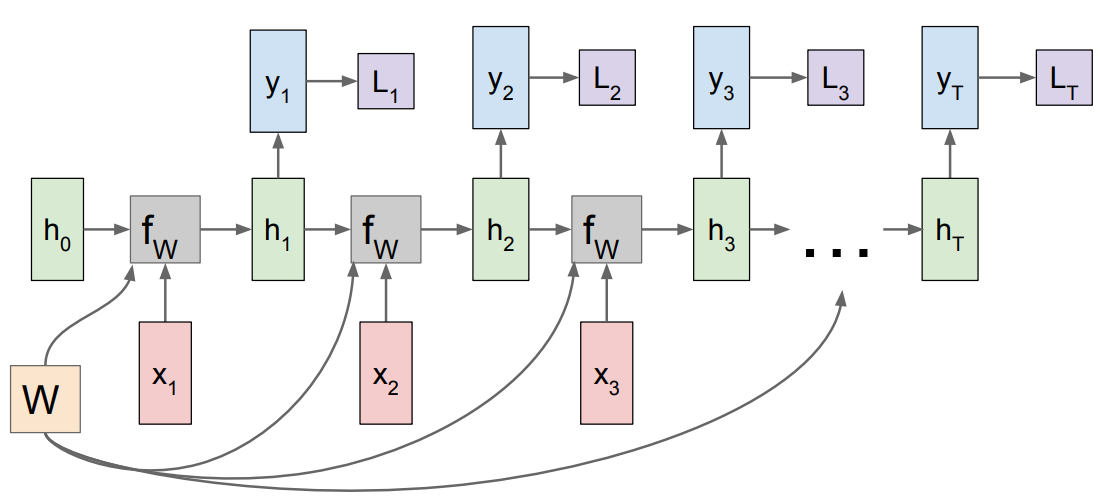
RNN의 역전파는 recurrent한 특징이 있어서 BPTT(BackPropagation Through Time)라고 하는 알고리즘을 사용한다.
마지막 step의 최종 loss만이 아니라, 각 step에서 backpropagation이 진행되는데서 차이가 있다.
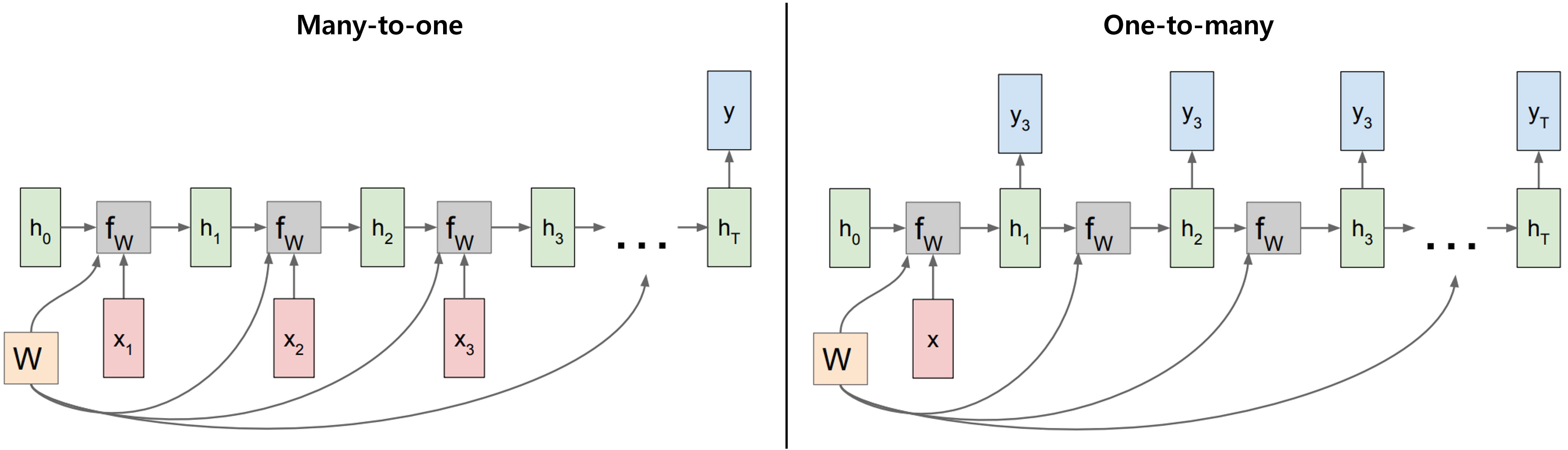
many-to-one과 one-to-many의 경우에도 아래와 같이 표현된다.
즉, hidden state을 업데이트하는 구조는 동일하지만, input과 output에 따라서 optional하게 변형시킬 수 있는 것이다.
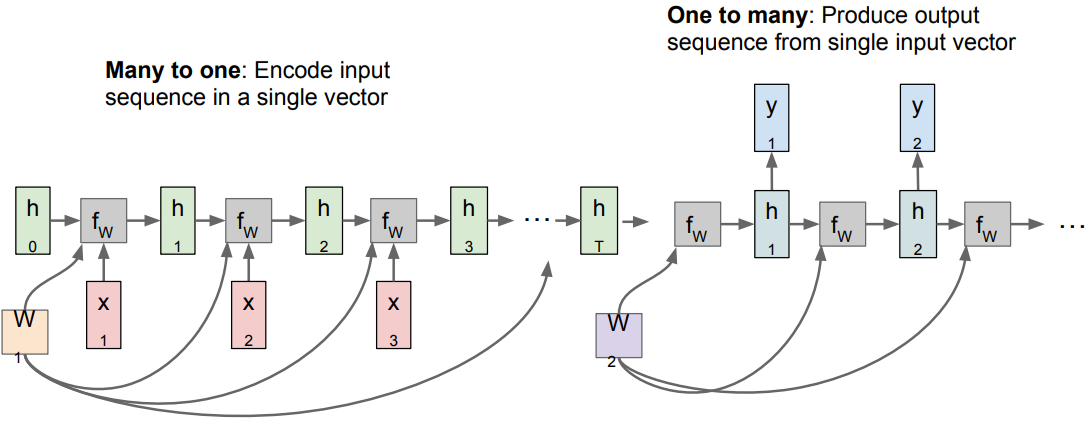
다음은 many-to-many(variable output)로 input과 output의 차원이 다르면서 여러 개이기 때문에, 앞의 두 방법(many-to-one과 one-to-many)을 결합해서 사용한다.
sequence-to-sequence(seq2seq)라고 부르며, 앞단의 many-to-one이 encoder, 뒷단의 one-to-many이 decoder역할을 한다.
Advantages and Disadvantages
지금까지 살펴본 Simple RNN의 장단점은 아래와 같다.
- 장점
- input의 길이와 상관없이 같은 weight으로 모델링이 가능하다.
- 따라서 Model size는 input의 크기에 영향을 받지 않는다.
- (문장이나 비디오 길이가 얼마가 되든 상관없음)
- 이전까지의 step들을 활용해서 현재 정보를 계산한다.
- 단점
- Recurrent computation은 느린편이다.
- 순차적인 계산이 필요하기에 병렬로 처리하기가 어려워진다.
- vanishing gradient 문제가 존재(다음 section에서 다룸)
- 이에 따라 long-range dependence를 반영하기 어렵다.
- (긴 문장을 넣어도 마지막 정도만 기억하고 앞단의 정보가 손실되어버림)
cs231n 강의에서는 python의 numpy만 이용해서 RNN을 구현한 코드도 제공하고 있다.
Gradient Flow
여기서는 Simple RNN이 backpropagation을 하는 과정에서 발생하는 vanishing gradient 문제에 대해 알아보자.
RNN은 $h_t$를 만들 때 $h_{t-1}$이 반영되기 때문에, 역전파가 진행될 때 $h_{t-1}$에 의한 gradient도 더해져 연쇄적으로 반영된다.
여기에서는 vanishing gradient를 다루기 위해 $W_{hh}$의 gradient만 유도해보자.
아래 그림은 기존 RNN을 다시 나타낸 것이다.
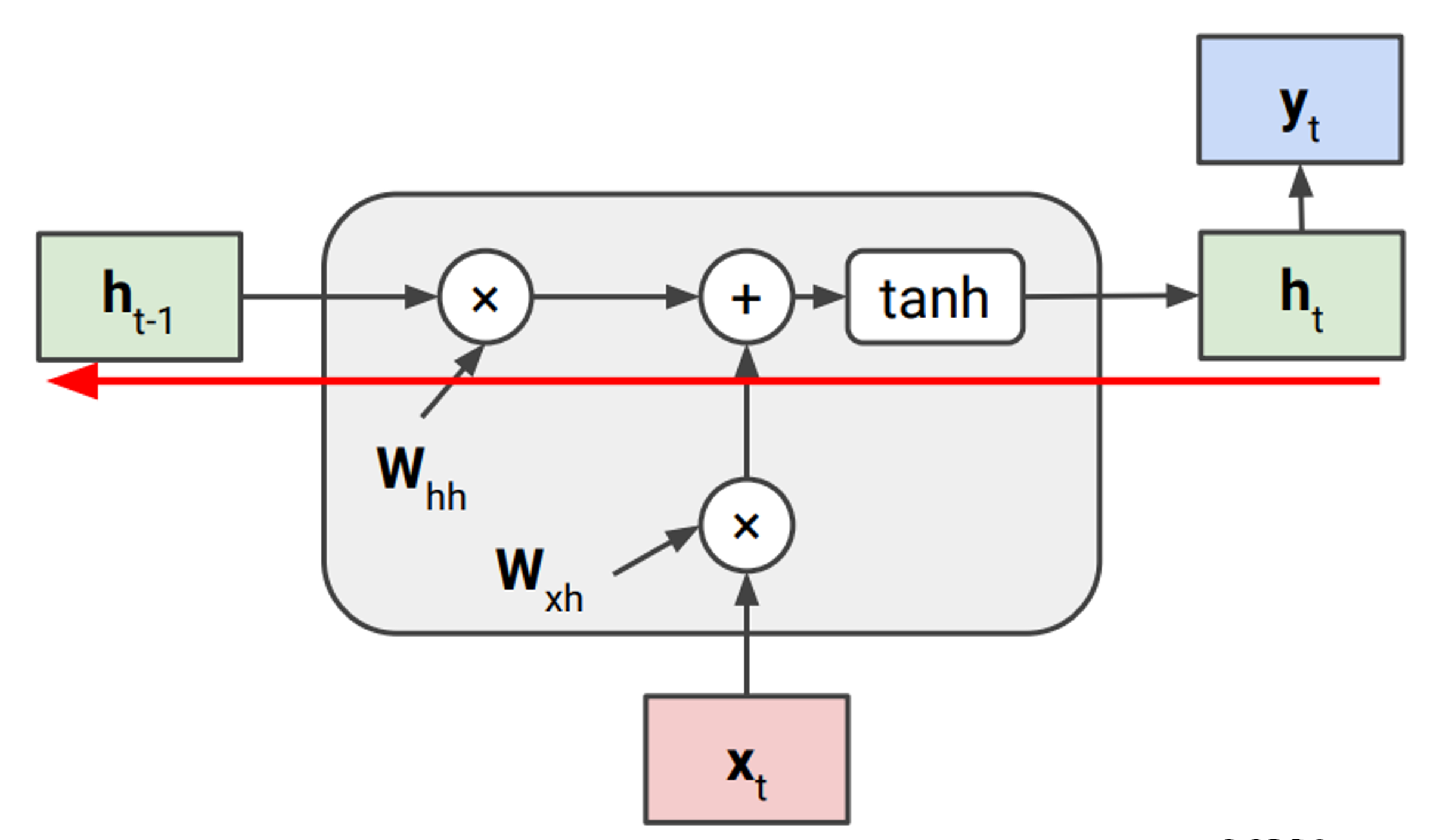
이전에 포스팅했던 backpropagation와 마찬가지로 chain rule이 적용된다.
즉 $h_t$에서 $h_{t-1}$로 가는 local gradient는 아래와 같이 계산된다.
$h_t=tanh(W_{hh}h_{t-1}+W_{xh}x_t)$
$\frac{\partial h_t}{\partial h_{t-1}}=tanh’(W_{hh}h_{t-1}+W_{xh}x_t)W_{hh}$
이를 기반으로 t 시점의 loss로부터 $W_{hh}$의 gradient인 $\frac{\partial L_t}{W_{hh}}$를 계산해보자.
\[\begin{align*} \frac{\partial L_t}{W_{hh}} &=\frac{\partial L_t}{h_t} \frac{h_t}{h_{t-1}} \frac{h_{t-1}}{h_{t-2}} ...\frac{h_{2}}{h_{1}} \frac{h_{1}}{W_{hh}} \\ &=\frac{\partial L_t}{h_t} (\prod_{k=2}^{t} \frac{\partial h_k}{\partial h_{k-1}}) \frac{h_{1}}{W_{hh}} \\ &=\frac{\partial L_t}{h_t} (\prod_{k=2}^{t} tanh'(W_{hh}h_{k-1}+W_{xh}x_k)W_{hh}) \frac{h_{1}}{W_{hh}} \\ &=\frac{\partial L_t}{h_t} (\prod_{k=2}^{t} tanh'(W_{hh}h_{k-1}+W_{xh}x_k))W_{hh}^{t-1} \frac{h_{1}}{W_{hh}} \\ \end{align*}\]이렇게 유도된 수식에서 중간에 2개의 term들을 한번 살펴보자.
첫번째는 $\prod_{k=2}^{t} tanh’(W_{hh}h_{k-1}+W_{xh}x_k)$로, tanh를 미분한 함수에 어떤 값이 들어간 형태로 도출된다.
아래 그림과 같이 tanh와 도함수를 보면, x=0에서 1이되며 양쪽으로 갈수록 0에 수렴하는 형태로 0~1사이 값을 가진다.
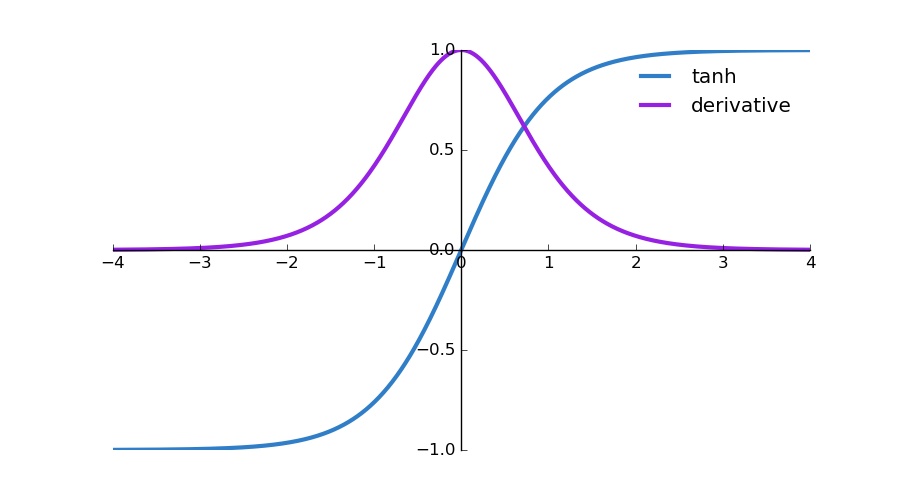
Source: Ronny Restrepo
이러한 값들이 t-1번 제곱되면 값이 계속 작아지고, 결국 vanishing gradients problem로 이어진다.
두번째는 weight matrix인 $W_{hh}^{t-1}$의 singular value(크기를 표현하는 상수)에 따라 문제가 생긴다.
- Largest singular value > 1이면, Exploding gradients
- Largest singular value < 1이면, vanishing gradients
앞서 RNN의 단점으로 언급했던 것 처럼, sequence가 길어짐에 따라서 gradient가 사라지거나 너무 커지는 문제가 생기기 때문에 control하기가 어렵다.
LSTM
위에서 다룬 RNN의 gradient flow에서 생기는 문제들을 개선한 것이 바로 LSTM (Long Short Term Memory)이다.
LSTM의 핵심은 각 step마다 hidden state($h_t$)만 업데이트하는 것이 아니라, cell state($c_t$)을 추가한 것이다.
이를 통해 기존 hidden state은 shor term memory를, cell state은 long term memory를 담당하도록 한다.
아래 그림처럼 cell state는 업데이트될때, 앞서 gradient flow에서 문제가 됐던 $W$를 곱하는 과정(FC)이 없다. 그렇기 때문에 cell gate에서는 sequence가 길어져 chain rule을 많이 타더라도 vanishing되지 않는다.
(*FC는 $W_{hh}h_{t-1}+W_{xh}x_t$ 연산을 fully-connected로 표기한 것)
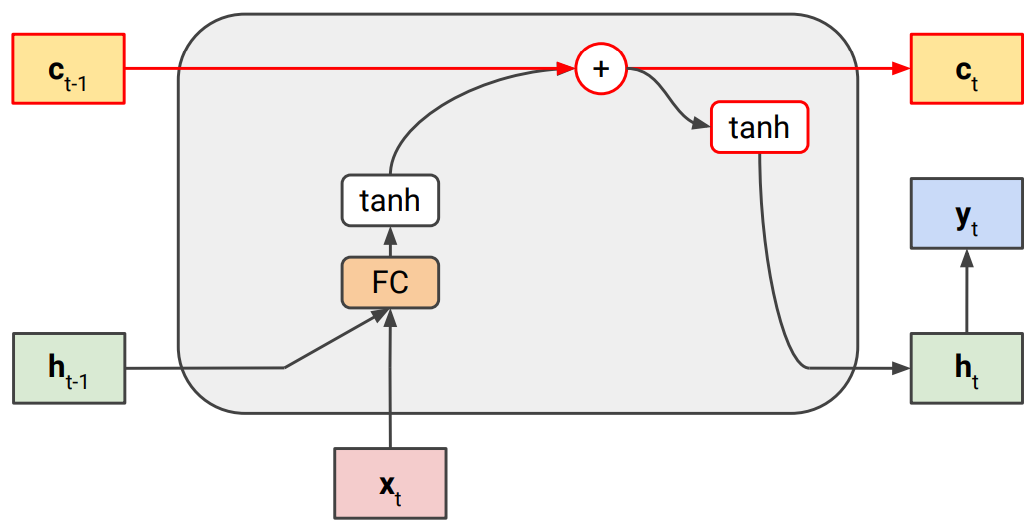
그리고 나서 아래 그림처럼 hidden state과 cell state와의 연계를 위해 gate를 넣어준다.
크게 3개의 gate가 존재하며, 역할에 대한 idea들이 담겨있다.
- Forget gate($f_t$): 이전까지의 정보를 얼마나 까먹을지 결정
- sequence가 길더라도, 끝날땐 끝나는 것으로 식별이 가능해야 한다.
- $\sigma$는 sigmoid로 0~1값을 가지므로, 지금까지 정보는 다 까먹어야 한다면 0에 가까운 값으로 활성화 될것이다.
- Input gate($i_t$): 현재 input과 hidden state을 얼마나 기억해둘지 결정
- 새로운 정보를 얼마나 받을지 결정하는 것이 필요하다.
- Output gate($o_t$): 다음 hidden state으로 넘어갈때 cell state에서 얼마나 정보를 받을지 결정
- 다음 hidden state은 현재의 정보(hidden state, input)와 지금까지의 정보(cell state)을 통해 결정된다.
즉, 이러한 구조를 통해 long term과 short term의 비중을 적절히 학습하도록 유도한 것이라 볼 수 있다.
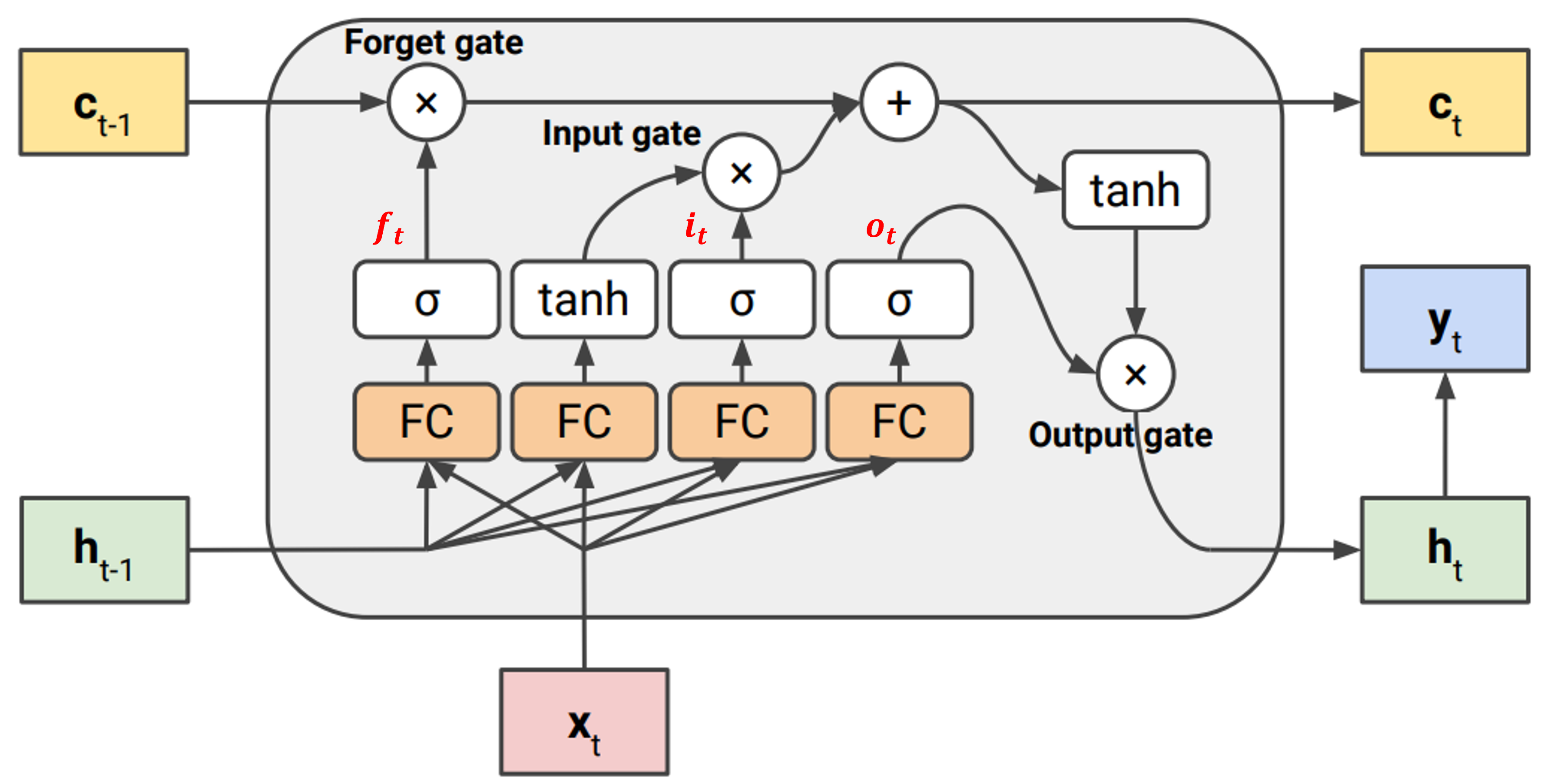
위 과정을 수식으로 표현하면 아래와 같다.
$c_t$의 수식을 보면, 첫번째 항은 이전 cell state($c_{t-1}$)를 forget gate($f_t$)가 관리해주고,
새로 들어온 정보($tanh(W_{new}x_t+U_{new}h_{t-1}+b_{new})$는 input gate($i_t$)가 제어해 주도록 설계되었다.
또한 $c_t$는 $c_{t-1}$에 paramter $W$를 직접 곱해져 계산되지 않고, 이전에서 값을 받아 사용하기 때문에 long term memory를 기억할 수 있게 되는 것이다.
$f_t=\sigma (W_fx_t+U_fh_{t-1}+b_f)$
$i_t=\sigma (W_ix_t+U_ih_{t-1}+b_i)$
$o_t=\sigma (W_ox_t+U_oh_{t-1}+b_o)$
$c_t=f_t\circ c_{t-1}+i_t \circ tanh(W_{c}x_t+U_{c}h_{t-1}+b_{c})$
$h_t=o_t\circ tanh(c_t)$
그러나 LSTM도 여전히 내부에 hidden state의 업데이트 과정은 포함되기 때문에(FC), vanishing/exploding gradient 문제가 발생할 가능성은 있다(훨씬 덜하다는 의미).
GRU
GRU(Gated Recurrent Units)는 LSTM과 비슷한 Idea에서 변형된 모델이다.
Paper는 Cho et al. (2014) Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation이다.
GRU는 LSTM과 달리 vanishing 문제 해결을 위해 cell state와 같은 별도의 state를 추가하지 않았다(그래서 Parameter가 더 적고 연산량이 빠르다).
대신에 아래 그림과 같이 hidden state을 update하는 과정에서, convex combination을 사용한다.
이를 통해 첫번째 항($(1-z_t)*h_{t-1}$)은 이전 state이 통과하도록 해준다(cell gate의 역할).
즉, $h_t$의 업데이트를 convex combination 통해 $W$에 영향을 받는 항과 그렇지 않은 항을 분리한 것이 핵심 idea이다.
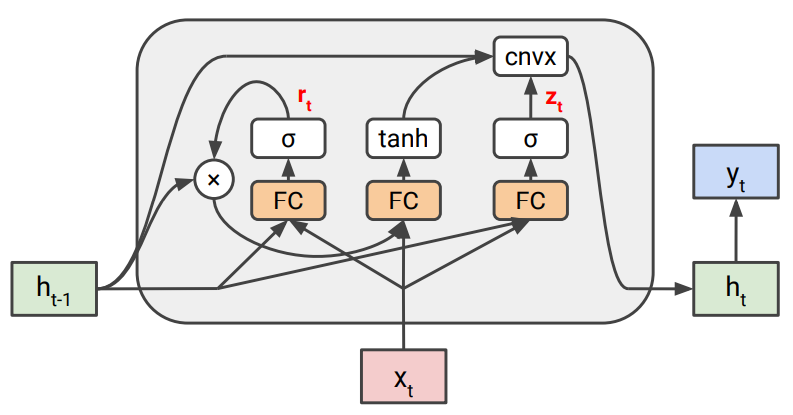
$r_t=\sigma (W_rx_t+U_rh_{t-1}+b_r)$
$z_t=\sigma (W_zx_t+U_zh_{t-1}+b_z)$
$h_t=(1-z_t)\circ h_{t-1}+z_t\circ tanh(W_hx_t+U_h(r_t\circ h_{t-1})+b_h)$
Reference
이 포스팅은 cs231n 수업(by Prof. Li Fei-Fei at Stanford University)과 Machine Learning for Visual Understanding (by 서울대학교 이준석 교수님) 수업을 듣고 공부하며 작성하였습니다.
https://cs231n.github.io/
http://viplab.snu.ac.kr/viplab/courses/mlvu_2021_2/index.html
https://ratsgo.github.io/natural%20language%20processing/2017/03/09/rnnlstm/
https://excelsior-cjh.tistory.com/184




댓글남기기