Yonggeun Shin

Yonggeun Shin

시행착오가 밑거름이 되는 공간

[cs231n] Training Neural Networks - part 2

업데이트:

개요

png

이전 포스팅에 이어서 마찬가지로 neural network를 training을 하는데 필요한 세부적인 기법들에 대한 내용이다.
Part2 은 Regularization, Optimization, Learning rate Scheduling, Batch Normalization에 대한 내용이 포함된다.


Regularization

Background

training을 할 때 자주 겪는 문제로 Overfitting이 있다. 우리는 새로운 데이터에도 잘 일반화될 수 있는 model을 개발해야하는 목표가 있다. training data에만 과적합되는 문제를 방지할 필요가 있다.
over fitting이 발생할 가능성이 높은 상황들은 아래와 같다.

  • training data의 noise까지 학습을 해버리는 경우
  • high-dimensional data와 noisy한 feature들을 다루는 경우
    • The curse of dimensionality
  • model의 복잡도가 불필요하게 높은 경우

The curse of dimensionality는 차원이 증가할 수록 같은 수준의 modeling을 위해 필요한 data의 수가 기하급수적으로 늘어나는 상황을 말한다.

png

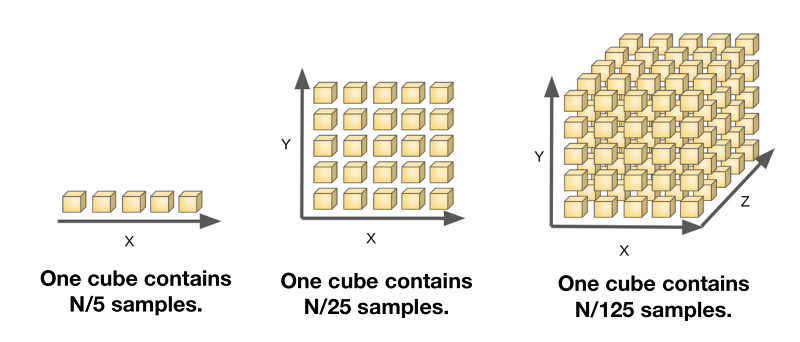
위 그림과 같이 1차원에서는 5개의 sample만으로 modeling이 가능했다면, 2차원은 $5^2$개, 3차원은 $5^3$개의 data가 필요하다. 하지만 우리의 데이터는 5개 밖에 없는데 dimension만 증가한다면, 편항될 가능성이 높고 이에 따라 overfitting이 생긴다.

이러한 상황은 이전 포스팅에서 다룬 kNN 알고리즘에 치명적으로 작용한다. 같은 데이터라도 dimension이 커질수록 distance가 증가하게 되어 잘 분류되지 않는 문제가 생긴다.

따라서 이러한 문제들을 방지하고 새로운 test data에도 잘 일반화시키기 위한 Regularization 기법들에 대해 알아보자.

Ridge, Lasso, Elastic Net

전통적인 방법은 additional한 term을 이용해 model에 규제(regularize)하여 model이 불필요하게 복잡해지는 것을 방지하는 방법이다. 이 term을 어떻게 구성하냐에 따라 Ridge, Lasso, Elastic net으로 나눠진다.

첫번째는 이전에 업로드한적 있는 Ridege Regression이다(L2 regularization 이라고도 한다).
Ridge Regression은 기존 regression의 loss function인 MSE에 L2-norm이라는 항을 추가하여 규제한다.

\[\begin{align*} J(\theta) & = (Y-X\theta)^T(Y-X\theta) + \sum_{i=0}^n \theta_i^2 \\ & = MSE(\theta) + \lambda \sum_{i=0}^n \theta_i^2 \end{align*}\]

즉, MSE를 minimize할 때, weight ($\theta$)이 과도하게 커지는 것을 방지한다.
weight이 커지는 것과 model의 복잡도가 증가하는 것은 강한 상관관계가 있기 때문에, 이러한 penelty term을 두어서 MSE를 줄이는 것이 L2-norm의 증가보다 효과가 클 경우에만 최적화된다.
L2-norm의 $\lambda$는 이 규제를 얼마나 강하게 줄 것인가에 대한 coefficient 값이다.

Lasso Regression는 penelty term으로 L1-norm을 추가하여 규제한다(L1 regularization 이라고도 한다).

\[J(\theta)= MSE(\theta) + \lambda \sum_{i=0}^n |\theta_i|\]

Elastic Net는 Ridge와 Lasso를 절충하여 penelty term으로 L1,L2-norm을 모두 추가하여 규제한다.

\[J(\theta) = MSE(\theta) +\lambda_1 \sum_{i=0}^n \theta_i^2 + \lambda_2 \sum_{i=0}^n |\theta_i|\] \[\lambda_1+\lambda_2 \leq 1\]

$\lambda_1=1$ 이면 Ridge, $\lambda_2=1$ 이면 Lasso로 동작한다.


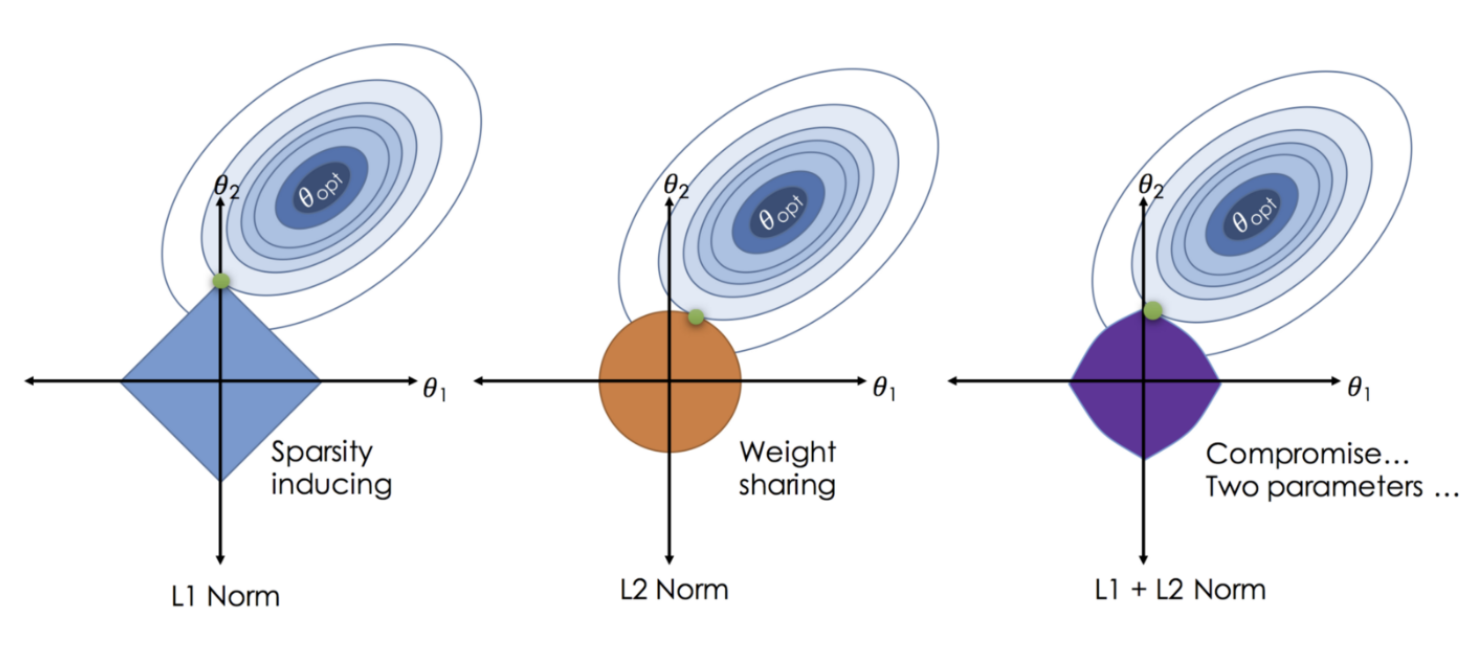
기존 Regression model에 penelty term을 두는 3가지 방법을 살펴보았다. 이런 규제가 실제로 어떻게 작용하는지 graphical하게 확인해보자.

png
*Source: https://soobarkbar.tistory.com/30

위 그림과 같이 penelty term의 영역 내에서만 weight이 업데이트 될 수 있다. 즉, optimal이 영역 밖에 있는 경우, 해당 영역과 가장 가까운 점에서 학습이 종료된다.

  1. Lasso(L1 Norm): 절대값으로 규제하므로 사각형의 구조를 갖는다.
    • 대부분 꼭지점으로 수렴하는 구조이므로, weight이 0이되도록 규제하는 것을 선호한다.
    • 따라서 noise에 조금 더 robust한 경향이 있다.
  2. Ridge(L2 Norm): 제곱으로 규제하므로 원형의 구조를 갖는다.
  3. Elastic Net(L1+L2 Norm): 사각형과 원형이 합쳐진 형태로 나타난다.

Neural Network에서는 이런 방식을 Weight decay라고도 표현한다.
하지만 Overfitting에 취약하기 때문에 더 다양한 방법들이 생겨났다.

Early Stopping

overffiting은 model이 trainig data에만 과하게 fitting되어 일반화가 잘 안되는 문제라고 했었다.
아래 그림처럼 학습이 진행됨에따라 training loss는 계속해서 감소하지만, validation set에서의 loss는 반등하는 지점이 있다. 이런 현상을 보통 overfitting되었다고 판단한다.

Early stopping은 이렇게 반등되는 시점에서 model 훈련을 종료시키는 방법이다.

png

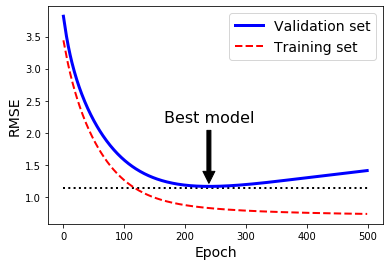
mini-batch를 이용한 SGD에서는 loss curve가 매끄럽게 감소하지 않기 때문에, 일정 시간(횟수)동안 관찰해보고 개선되지 않으면 stop하는 방법을 사용할 수 있다.

Dropout

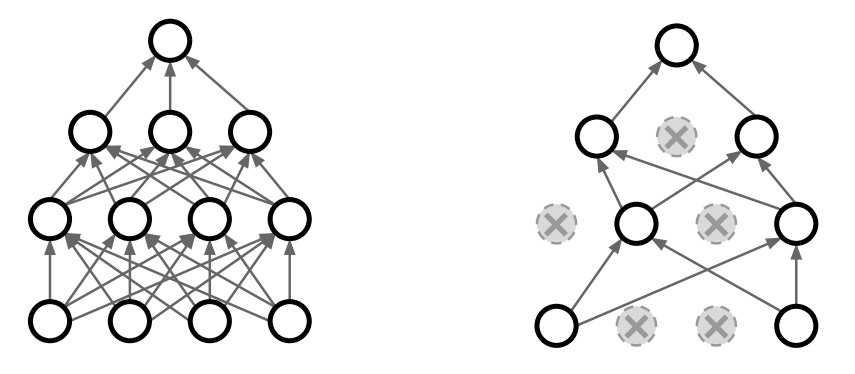
Neural Network에 특화된 방법으로 Dropout이라는 기법이 있다.
이는 random하게 일부 node들을 network에서 제외하고 학습시키는 방법이다. 얼마나 drop 시킬지를 parameter로 결정해야한다(e.g. 0.5이면 절반을 제외한다).

png

이러한 방법을 이용하면 다음과 같은 효과가 있다.

  • 임의의 node를 제외함으로써 한 feature에 영향력이 집중되는 현상을 방지한다.
  • ensemble model의 효과를 낼 수 있다.
    • forward마다 다른 node들을 가진 network가 학습되기 때문이다.

Dropout은 Pytorch나 Tensorflow와 같은 프레임워크에서 제공하고 있어서 구현할 일은 없지만, 원리를 아래 코드를 통해 살펴보자.

png

p라는 확률 값으로 masking을 해서 일부 node를 제외시킨다. 이때 살아남은 노드에는 제외한 비중 p만큼 값을 키워주어야 한다.
원래 network에서 node만 제외하면 weight자체가 작아져서 잘 분류가 안되기 때문에, scale을 맞춰주어야 하기 때문이다.
Test를 할때는 모든 node를 사용해서 inferece 한다.

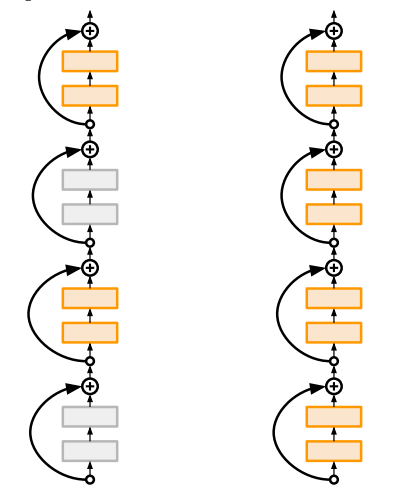
Stochastic Depth

Stochastic Depth는 dropout과 비슷하긴 한데, 일부 Layer를 건너뛰는(Depth 관점) 방법이다.
아래 그림처럼 training(왼쪽)할 때 일부 layer를 random하게 건너뛰도록 하고, testing(오른쪽) 할 때는 전체 network를 사용하여 inference한다.

png

Data Augmentation

Data Augmentation은 우리가 가진 input data를 label은 유지한채로 여러가지 방법으로 augment해서 학습 효율을 높이기 위한 기법이다.
여기서 학습 효율을 높인다는 의미는 다음과 같다.

  • 조금 다른 이미지에도 잘 일반화 되도록(training data에만 과적합되지 않도록) 하도록 한다.
  • training data가 적을 경우 확장시킬 수 있다.

실제로 augment 기법들은 무수히 많고, domain knowledge에 따라 달라질 수 있다.
여기서는 몇가지만 살펴보자.

  • Horizontal(Vertical) Flips

png

상하좌우로 뒤집어 같은 고양이를 다른 각도의 이미지로 학습시킬 수 있다.

  • Random Crops & Scaling

png

기존 사진의 일부분을 짜르거나(Random Crops), 사진을 확대 또는 축소(Scaling)하는 방법도 사용해볼 수 있다.
참고로 이러한 기법을 적용했던 ResNet에서는 Training 뿐 아니라 Testing 할때도 데이터를 여러가지로 augment해서 predict하고 이 값들의 다수결 투표를 통해 최종 성능을 측정했었다.

  • Cutout

png

Cutout은 이미지의 일부 영역을 무작위로 잘라내는 방법이다.
Crops과 달리 Cutout은 자르고 남은 이미지를 사용한다. 자른다는 것은 일부 영역의 pixel값들을 zero로 채워넣는 것을 의미한다.
small dataset에서는 잘 동작하지만, large scale에서는 불필요한 연산이 많아져 잘 쓰지 않는다.

  • Color Jitter

png

color jitter는 간략하게는 색상에서 대비(contrast)와 밝기(brightness)를 random하게 조정하는 기법이다. 즉, 같은 고양이가 다른 조명에서 찍혔을 때를 고려한 아이디어이다.

좀더 세부적으로는 color을 구성하는 RGB 값을 HSL(Hue, Saturation, Lightness)값으로 변환하여 조정해주고, 다시 RGB로 변환하여 data를 만드는 방식이다.
HSL을 쓰는 이유는 RGB를 바로 random하게 바꾸면 색의 변화를 직관적으로 알기 어렵기 때문에, HSL 값은 인식하기가 편하기 때문(ex. 밝기를 줄인다거나)이다.


Batch Normalization

이전 포스팅에서 Data Preprocessing을 통해 zero-centered한 data가 학습에 유리하다는 것을 알게 되었다.
그런데 input data에 대한 것 뿐만아니라, intermediate layers 들에서도 zero-centered하게 할 수는 없을까? 라는 물음에서 생겨났다.
Batch Normalization은 layer 중간 중간에서 강제적으로 output을 normalize시키는 방법이다.

이를 위해 아래 그림처럼 각 mini-batch의 input data가 N개이고 차원이 D일 때, 평균(mean)과 분산(variance)를 이용해서 normalize해주는 방법을 사용한다.

png

하지만 forward와 backward를 반복하여 학습하는 Nearual Network인데, 인위적으로 normalize를 해버리면 training이 되지 않을 것이다.
이를 위해 다시 원래의 값으로 변환해주는 수식하나가 추가된다.

png

수식에는 두개의 parameter가 존재하는데, 표준편차 역할을 하는 scale factor($\gamma$)와 평균 역할을 하는 shift factor($\beta$)이다.
두 parameter는 학습가능한 변수로서 backpropagation을 통해 학습된다.
이를 통해 BN(Batch Normalization)은 학습 가능한 layer가 되고, training이 되지 않는 문제를 방지할 수 있다.

정리하면 아래와 같다.

png

  1. mini-batch data로 부터 mean과 variance 계산
  2. normalize 실행 ($\epsilon$은 0으로 나눠지는 것을 방지하기 위한 값)
  3. 학습가능한 scale, shift parameter 추가

그리고 실제 사용할때는 아래 그림과 같이 activation function 바로 이전, 또는 FC와 Conv layer 바로 다음에 사용된다.
이전 포스팅에서 언급한 바와 같이 activation function의 input이 zero-centered data가 들어가야 zig-zag하지 않고 효율적인 미분이 가능하기 때문이다.

png

Test할 때는 어떻게 해야할까??
test는 batch가 없기 때문에 mean과 variance를 계산할 수 없다.
그래서 training data의 평균과 분산(고정값)을 이용하여 연산을 수행한다.
결국, test에서의 BN layer는 mean, varaince는 고정값이며, train된 2개 파라미터를 사용하므로 linear한 연산만 수행하고 넘어가는 것과 같다.

Batch Normalization을 이용하면 Layer 별로 zero-centered를 유지할 수 있기 때문에 다양한 장점이 생긴다.

  • Improves gradient flow through the network
  • Allows higher learning rates
  • Reduces the strong dependence on initialization
  • Acts as a form of regularization
  • slightly reduces the need for dropout, maybe
  • 계산량도 그닥 복잡해지지 않음

거의 모든 면에서 장점을 가지지만, test할때 training data의 mean과 variance를 그대로 사용하는 것에서 몇가지 약점이 생긴다.

  • training data가 i.i.d가 아닌 경우
  • test하려는데 data 분포가 바뀐 경우 (시간이 많이 흘렀다거나)
  • mini-batch size가 너무 작아서 mean, variance가 정확하지 않은 값인 경우

이를 개선하기 위해 Batch Renormalization 논문이 생겨나기도 했다.


Optimization

이전 포스팅에서 optimization에 주로 사용되는 방법인 SGD(Stochastic Gradient Desenct)와 여러가지 challenge들에 대해 배웠었다.
여기서는 문제점들을 다시 리뷰하고 이를 개선하기 위한 다양한 기법들에 대해 알아보자.

Problems with SGD

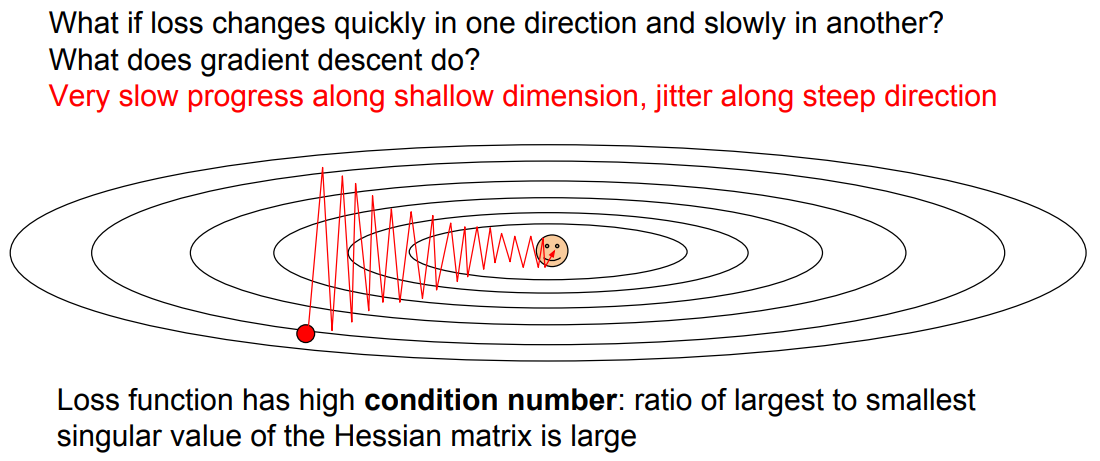
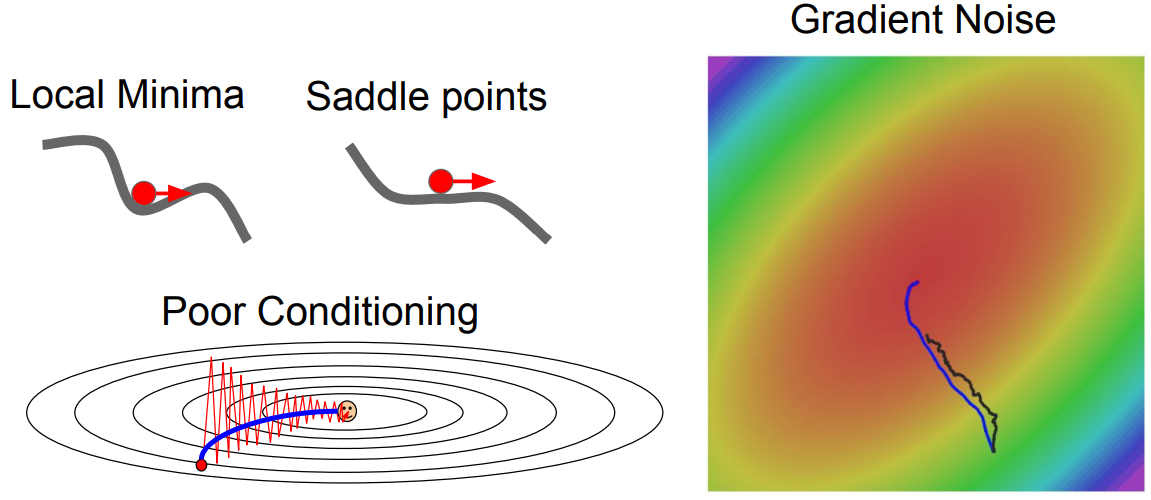
  1. Jittering

첫번째 문제는 Jittering으로, loss function의 한쪽 gradients가 상대적으로 큰 상황에서 optimize를 할때 zig zag 형태로 비효율적인 학습이 발생하는 것을 의미한다.

png

  1. Local optimum and Saddle points

두번째 문제는 이전 포스팅에서도 논의했었지만, Saddle point는 local minimum도 아닌데 gradient가 0이 되어 학습이 종료되는 이슈가 있다.
이 saddle points는 high dimensional data에서 흔히 볼 수 있는 현상이다.

  1. Inaccurate Gradient Estimation

세번째 문제는 SGD에 이용되는 mini-batch에 noise가 많이 포함된다면, gradient가 부정확할 수 있다는 것이다.
전체 training data가 large-scale로 갈 수록 문제가 심해지는데, train set 대비 mini-batch size의 차이가 커질 수록 일반화가 어려워지기 때문이다.

SGD + Momentum

앞서 살펴본 문제(특히 Saddle point)를 해결하기 위해 물리학적인 측면에서 발전된 아이디어가 Momentum이다.
이는 관성(inertia)을 이용해서 gradient가 0이 되더라도 움직이던 방향의 속도를 유지해줌으로써, saddle point를 넘어가도록 해주자는 아이디어이다.
이 관성은 아래 수식처럼 속도를 표현하도록 momentum 항 $v$를 추가하게 된다.

png

기존 SGD와 달리 gradient들을 누적해서, 누적된 값으로 update해주는 방식이다. 따라서 지금까지 움직였던 방향으로 힘(가속도)을 더 받을 수 있게 된다.
이를 통해 아래그림 처럼 Local minimum이나 saddle point를 탈출할 수 있고, gradient의 noise도 조금 감소하는 효과를 볼 수 있다.

png

AdaGrad

AdaGrad는 조금 다른 접근 방식으로, gradient를 적응적으로(Adaptive) 다뤄보겠다는 아이디어이다.
앞서 언급한 Jittering 문제를 해결하고자, gradient를 Element-wise로 scaling하는 방법을 사용한다.
Jittering 문제가 graident가 큰 쪽(경사가 깊은)으로만 너무 step size가 커져서 zig-zag되는 것이였기 때문에, 각 gradient scale을 맞춰서 비교적 균일하게 움직이도록 하는 것이다.
아래 그림의 코드를 보면 직관적으로 이해가 되는데,

png

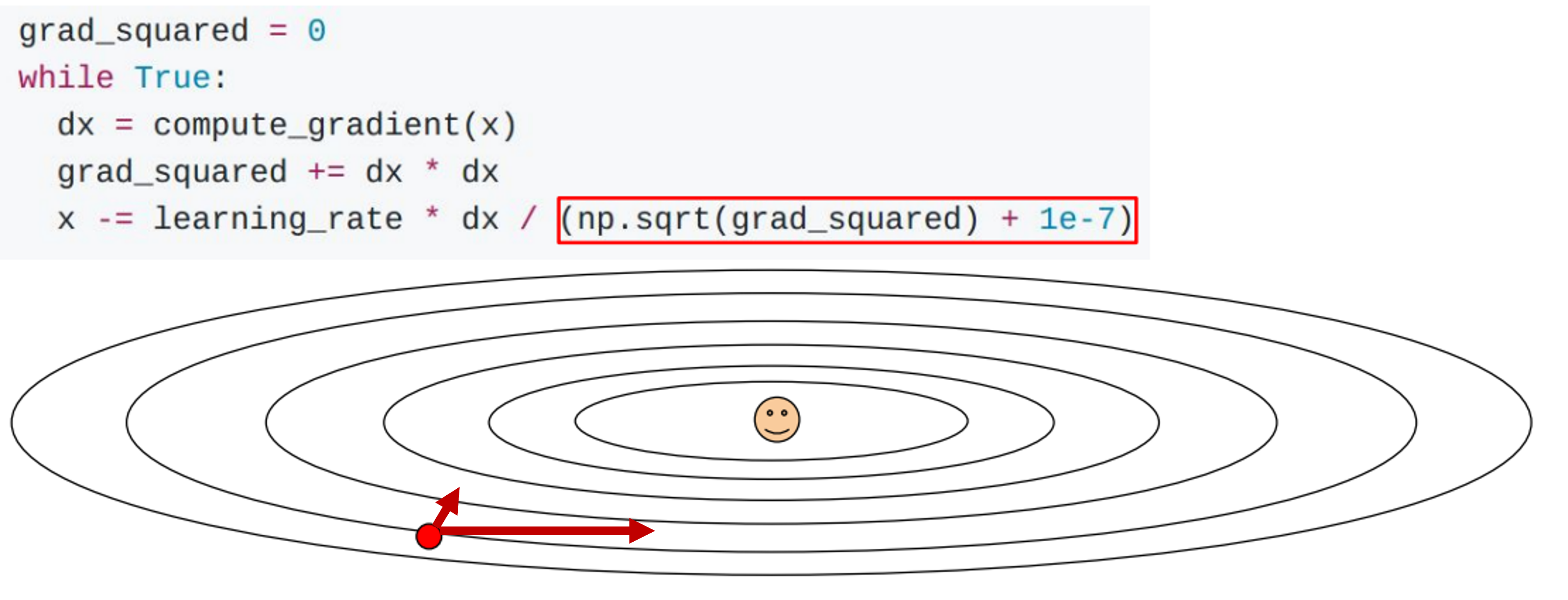
gradient(dx)를 제곱해서 누적하고 이 값을 다시 square root를 해서 나눠준다.
여기서 누적하는게 point인데, 즉, gradient가 컸던 것들은 큰 값으로 나누어져 작게 update가 되고 반대로 작은 값들은 크게 update가 되는 것이다.
이런 이유로 AdaGrad는 Learning rate을 조절하는 방법이라고도 한다.

그러나 이런 방법은 학습이 진행됨에 따라 step size를 계속 감소시켜 업데이트가 너무 느리게되는 문제가 생긴다.

RMSProp (Leaky AdaGrad)

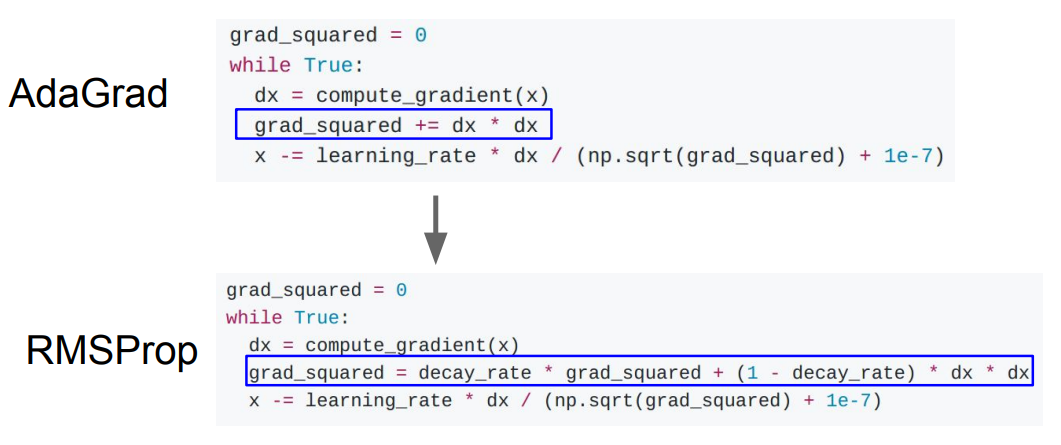
AdaGrad의 step size 감소 문제를 해결한 것이 RMSProp (Leaky AdaGrad)이다.
아래 그림처럼 그냥 누적하지 않고 decay rate을 추가한다. 이를 통해 과거의 값들에만 의존하지 않고 현재 값들의 추세도 반영할 수 있다.
예를 들어 decay_rate=0.9라고 해보자. 경사가 깊은 곳을 다 내려왔을 때 최근 gradient는 감소할 것이다. 따라서 이 간이 반복되면 누적된 grad_squared도 다시 작아질 것이다.

png

Adam

Adam은 현재 가장많이 사용하는 optimizer로, SGD + Momentum과 RMSProp을 절충한 방법이다.
특별히 다른 방법은 없고 두 방법을 합친것이기에 아래 코드를 보면 잘 이해가 된다.

png

first_moment는 SGD + Momentum에서 누적했었던 속도 $v$ 이였고, 관성을 기반으로 원래 진행하는 방향의 힘을 받을 수 있었다.
second_moment는 바로 살펴보았던 RMSProp에서 gradient scaling을 위한 grad_squared를 누적하는 수식이였다.
하지만 second_moment를 바로 나눠주었던 RMSProp과 달리 Bias correlation이 필요하다. 처음에는 moment들이 누적되지 않았기 때문에 0에 가까운 값을 갖는데, 이 상황에서 바로 moment를 나눠주면 step size가 너무 커지게 되는 문제가 발생한다. 이를 위해 약간의 보정을 해줬다고 이해할 수 있다.

실제로 beta1=0.9, beta2=0.999, learning_rate=1e-3 or 5e-4 정도를 사용하면 여러 model에서 잘 학습이 된다는 경험적인 의견도 있다.

First, Second-order Optimization

지금까지 살펴봤던 optimization 방법들은 First-order Optimization이다.
즉, 어느 한 점에서 미분을 하고 그 방향으로 이동시키는 과정을 반복했었다. 따라서 미분이라는 것은 그 점에서의 linear approximation이 되는 것이다.

png

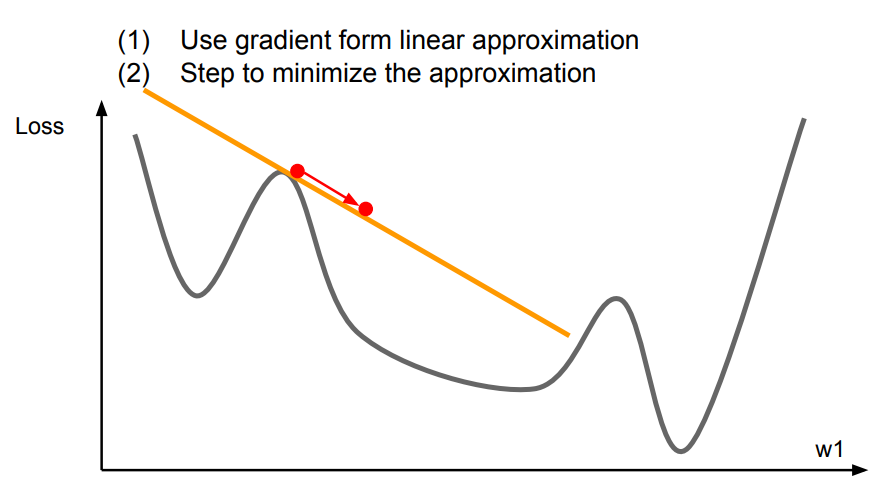
이러한 관점에서 Second-order Optimization은 linear가 아닌 2차식으로 approximation하는 방법을 의미한다.
아래 그림처럼 1차식 보다는 보다 Loss function에 근접하게 approximate할 수 있는 장점이 있다.
Loss function을 vector로 두번 미분하게 되면 Hessian matrix이 도출된다.

png

png

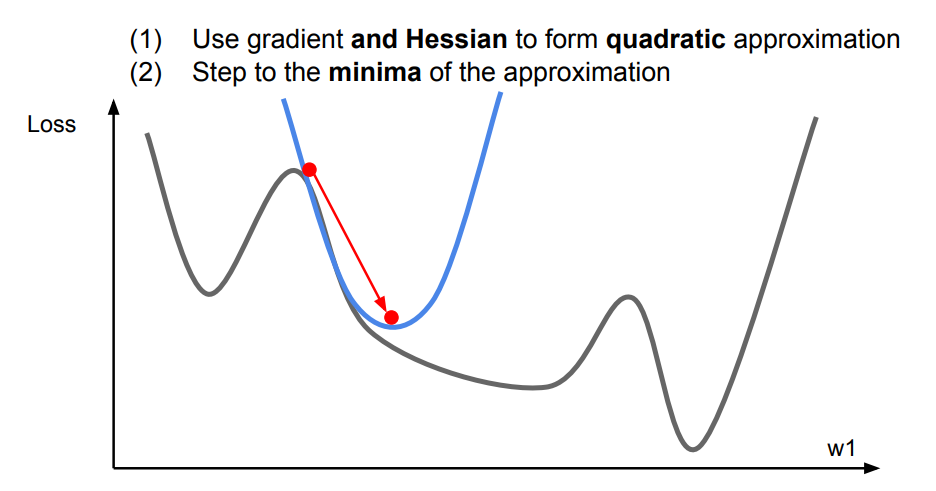
이러한 방식에는 장단점이 존재한다.

  • 장점
    • update되는 수식을 보면, 기존에 optimizer에서 필요했던 parameter나 learning rate이 필요없어 간단해진다.
    • First-order보다 더 정확한 gradient를 도출할 수 있다.
  • 단점
    • Hessian은 matrix라 $O(N^2)$의 연산량이 필요하므로, inverse($H^{-1}$) 계산에는 계산복잡도가 $O(N^3)$이 된다.
    • deep learning에서는 N이 매우 크기 때문에 계산복잡도가 기하급수적으로 증가한다.

이런 치명적 단점 떄문에 Second-order는 잘 쓰이지 않는다.


Learning Rate Scheduling

Learning rate scheduling은 Optimization에서도 중요한 hyperparameter로 작용했던 Learning rate을 어떻게 조정할지에 대한 전략에 대한 내용이다.
아래 그림과 같이 learning rate을 어떻게 설정하냐에 따라 performance가 달라지는 것을 알 수 있다.

png

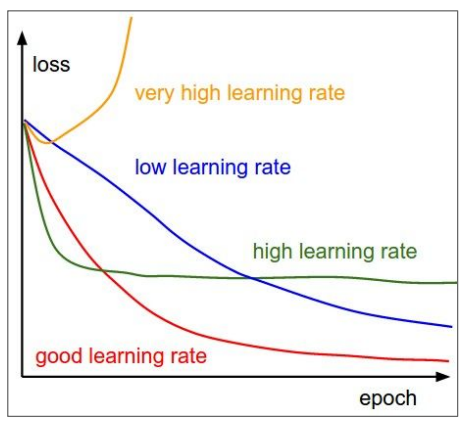
따라서 적절한 learning rate를 찾는것이 매우 중요한데, 초기값을 어떻게 설정할지(initial)와 어떻게 줄여나갈지(decay)에 따라 전략이 달라진다.
일반적으로 initial값을 크게 잡고, 점점 decay하도록 구성하는데, 아래와 같이 Cosine, Linear, Inverse Sqrt 등이 있다.

png

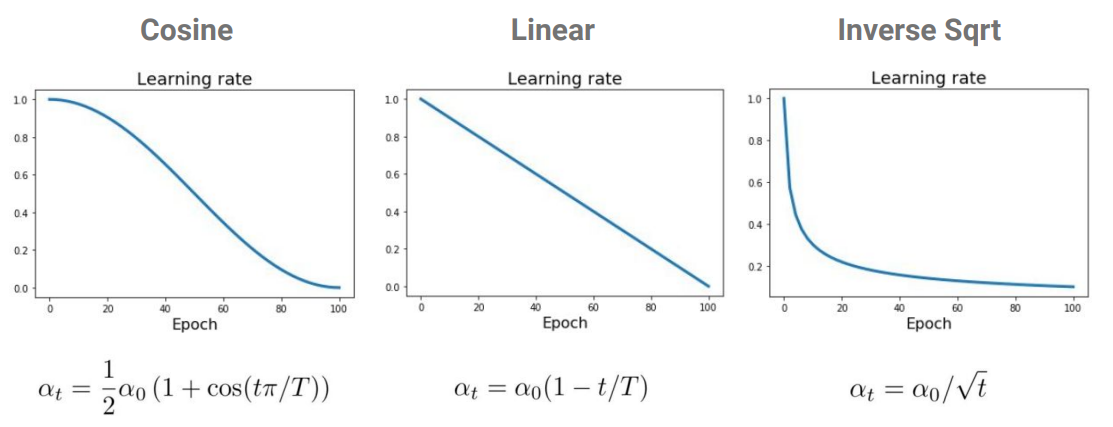
위 수식에서 $\alpha_t$는 epoch $t$에서의 learning rate을 의미하고, $\alpha_0$는 initial 값, $T$는 전체 epoch의 수 이다.


Reference

이 포스팅은 cs231n 수업(by Prof. Li Fei-Fei at Stanford University)과 Machine Learning for Visual Understanding (by 서울대학교 이준석 교수님) 수업을 듣고 공부하며 작성하였습니다.

https://cs231n.github.io/

http://viplab.snu.ac.kr/viplab/courses/mlvu_2021_2/index.html

https://datapedia.tistory.com/15

https://cvml.tistory.com/5#rp

댓글남기기

참고