[Handson ML] 부스팅(Boosting)과 스태킹(Stacking) - 앙상블
업데이트:
개요

이번 포스팅에서는 약한 모델을 연속적으로 보완해나가며 정확도를 개선하는 부스팅과 스태킹 알고리즘에 대해 알아보자.
부스팅(Boosting)
부스팅(Boosting)은 약한 학습기를 여러개 연결하여 강한 학습기를 만드는 앙상블 방법을 말한다.
기본 아이디어는 앞의 모델을 보완해 나가면서 일련의 예측기를 학습시키는 것이다.
1. 아다부스트
아다부스트(AdaoBoost)는 Adaptive Boosting의 줄임말로 이전 모델이 과소적합했던 훈련 샘플의 가중치를 더 높이는 방식이다.
이렇게 하면 새로운 예측기는 학습하기 어려운 샘플에 점점 더 맞춰지게 될 것이다.
과정은 다음과 같다.
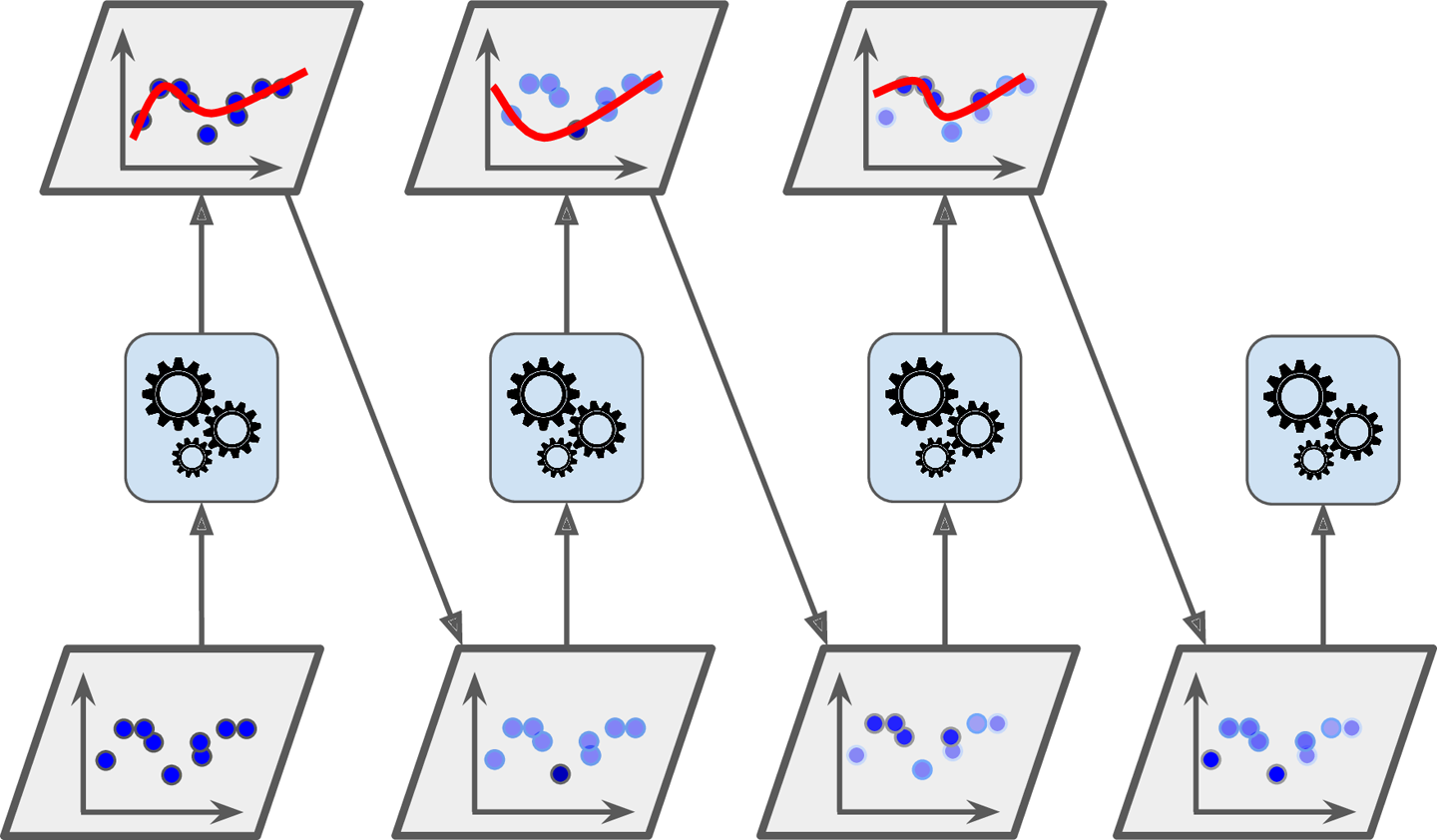
- 기반이 되는 첫 번째 분류기를 훈련 데이터셋으로 훈련시키고 예측값을 만든다.
- 잘못 분류된 훈련 샘플의 가중치를 상대적으로 높인다.
- 업데이트된 가중치를 사용해 두번째 분류기를 훈련세트로 훈련하고 다시 예측값을 만든다.
- 2~3과정 반복
다음은 moons dataset을 이용하여 5개의 연속된 SVM분류기의 Adaboost모델을 for문을 통해 수동적으로 가중치를 더해가는 과정을 임시로 구현한 코드이다.
코드를 보면 처음 가중치는 모두 1이고 잘못 분류된(y_pred != y_train)샘플에 대하여 (1+learning_rate)를 계속해서 곱해나간다.
그 후에 SVM분류기에 훈련 데이터를 다시 fit할때 sample_weight옵션에 업데이트된 가중치를 부여해주는 방식이다.
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 결정경계 plotting 함수 정의
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import numpy as np
def plot_decision_boundary(clf, X, y, axes=[-1.5, 2.5, -1, 1.5], alpha=0.5, contour=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if contour:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", alpha=alpha)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", alpha=alpha)
plt.axis(axes)
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
from sklearn.svm import SVC
m = len(X_train)
plt.figure(figsize=(11, 4))
for subplot, learning_rate in ((121, 1), (122, 0.5)):
sample_weights = np.ones(m)
plt.subplot(subplot)
for i in range(5):
svm_clf = SVC(kernel="rbf", C=0.05, gamma="scale", random_state=42)
svm_clf.fit(X_train, y_train, sample_weight=sample_weights)
y_pred = svm_clf.predict(X_train)
print(sample_weights[:10]) # 가중치가 더해가는 과정 출력, 10개만
sample_weights[y_pred != y_train] *= (1 + learning_rate)
plot_decision_boundary(svm_clf, X, y, alpha=0.2)
plt.title("learning_rate = {}".format(learning_rate), fontsize=16)
if subplot == 121:
plt.text(-0.7, -0.65, "1", fontsize=14)
plt.text(-0.6, -0.10, "2", fontsize=14)
plt.text(-0.5, 0.10, "3", fontsize=14)
plt.text(-0.4, 0.55, "4", fontsize=14)
plt.text(-0.3, 0.90, "5", fontsize=14)
plt.show()
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 2. 1. 1. 2.]
[1. 1. 1. 1. 1. 1. 4. 1. 1. 2.]
[1. 2. 1. 1. 1. 1. 4. 1. 1. 2.]
[2. 4. 1. 1. 1. 1. 4. 1. 1. 2.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1.5 1. 1. 1.5]
[1. 1. 1. 1. 1. 1. 2.25 1. 1. 1.5 ]
[1. 1. 1. 1. 1. 1. 3.375 1. 1. 1.5 ]
[1. 1.5 1. 1. 1. 1. 5.0625 1. 1. 1.5 ]
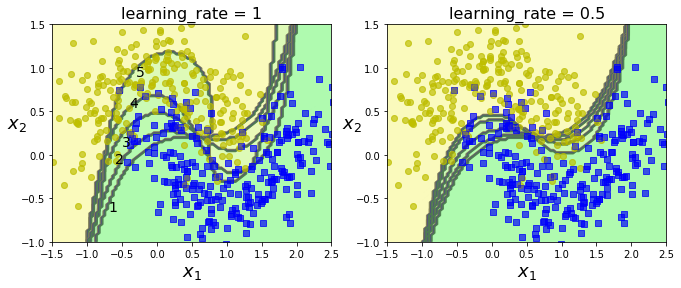
첫번째부터 다섯번째까지 학습을 진행할수록 더 정확하게 분류되는 것을 확인할 수 있다. 하지만 learning_rate이 1보다는 0.5인 경우가 더 일반화가 가능한 결과를 가져다준다.
이러한 방식은 이전에 배운 경사하강법과 비슷한면이 있다.
경사하강법은 cost function을 최소화하도록 예측기의 파라미터를 조정하고,
아다부스트는 예측이 더 정확해지도록 앙상블에 가중치를 조정한다.
무튼 아다부스트도 마찬가지로 모든 예측기가 훈련을 마치면, 배깅이나 페이스팅과 비슷한 방식으로 최종 예측을 만드는데, 가중치가 적용된 훈련세트의 전반적인 정확도에 따라 예측기마다 다른 가중치가 적용된다.
아다부스트는 이전의 학습에 대해 보완해나가는 연속적인 학습기법이므로, 병렬(분산)화를 할 수 없는 단점이 있다. 결국 배깅이나 페이스팅만큼 확장성이 높지 않다.
1-1. 아다부스트의 알고리즘
앞에서는 단지 learning_rate을 곱해나가는 방식으로 구현해봤지만, 좀더 자세히 들여다 보자.

-> j번째 예측기의 가중치가 적용된 에러율
위 식은 초기 가중치의 합에 대한 예측과 샘플이 다른 가중치의 합을 나타낸다.
- w(i)는 초기에 1/m(m : 훈련세트 수)로 초기화
- 첫번째 예측기 학습
- 위 식을 이용해 가중치가 적용된 에러율(r1)이 훈련세트에 대해 계산
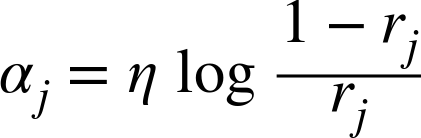
- 앞에서 구한 에러율(rj)와 학습률(η)을 이용해 예측기의 가중치(αj)계산
예측기가 정확할수록 에러율(rj)이 낮아져 가중치(αj)가 높아지게 된다.
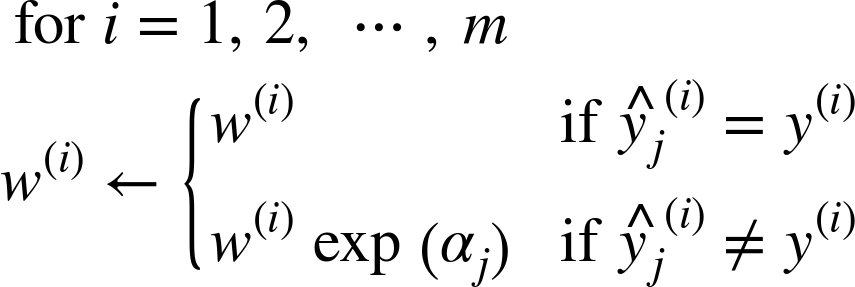
- 위 식을 이용해 각 샘플의 가중치를 업데이트한다.(즉, 잘못분류된 샘플의 가중치가 증가)
- 모든 샘플의 가중치 정규화(시그마w(i)로 나눔)
- 업데이트된 가중치를 사용해 새 예측기를 훈련
- 3~7의 과정 반복
- 지정된 예측기의 수에 도달하거나 완벽한 예측기가 제작되면 중단.
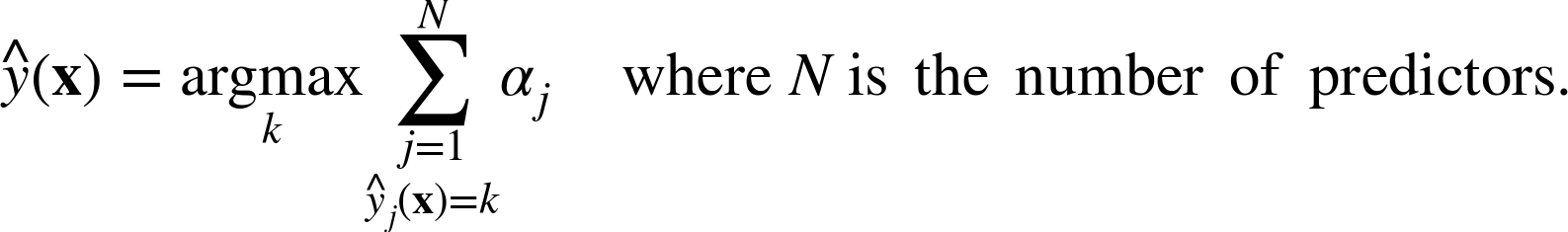
아다부스트는 예측을 할때 모든 예측기의 예측을 계산하고 예측기 가중치(αj)를 더해 예측결과를 만든다.
가중치 합이 가장 큰 범주가 예측결과가 된다.
사이킷런은 SAMME라는 아다부스트의 다중 범주 버전을 사용한다. 범주가 2개(이진분류)라면 SAMMEE가 아다부스트와 동일하다.
예측기가 범주에 속할 확률(predict_proba())을 계산할 수 있다면, SAMME.R(Real)이라는 변종을 사용한다.
이는 예측값 대신 확률에 기반하며 성능이 더 좋다.
SAMMEE와 SAMME.R의 가중치 계산 알고리즘은 차이가 있으므로 찾아보길 권장한다.
다음은 AdaBoostClassifier를 사용하여 moons dataset에 훈련시킨 200개의 아주 얕은(max_depth=1)결정트리 예측기의 결정 경계이다.
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
ada_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1), # 트리 노드 1개
n_estimators=200, # 200개 앙상블
algorithm='SAMME.R',
learning_rate=0.5,
random_state=42)
ada_clf.fit(X_train,y_train)
AdaBoostClassifier(algorithm='SAMME.R',
base_estimator=DecisionTreeClassifier(class_weight=None,
criterion='gini',
max_depth=1,
max_features=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
presort=False,
random_state=None,
splitter='best'),
learning_rate=0.5, n_estimators=200, random_state=42)
plot_decision_boundary(ada_clf, X, y)
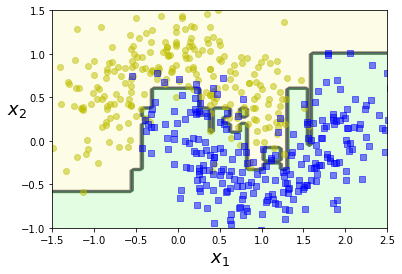
아다부스트 앙상블 모델이 훈련세트에 과대적합되면 추정기 수를 줄이거나 추정기에 규제를 주는 방법을 고려해보자.
2. 그래디언트 부스팅
그래디언트 부스팅(Gradient Boosting)도 아다부스트 처럼 이전 예측기의 오차를 보정하도록 예측기를 순차적으로 추가하지만,
반복마다 샘플의 가중치를 수정하는게 아니라(like 아다부스트) 이전 예측기가 만든 잔여오차(residual error)에 새로운 예측기를 학습시킨다.
간단한 예로 결정트리를 기반으로 회귀문제를 풀어보자.
노이즈가 섞인 2차곡선 형태의 훈련세트를 생성한다.
np.random.seed(42)
X = np.random.rand(100, 1) - 0.5
y = 3*X[:, 0]**2 + 0.05 * np.random.randn(100)
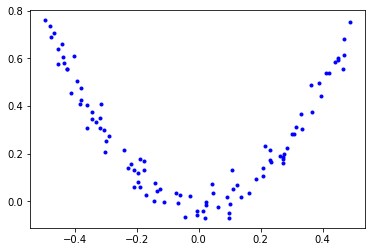
생성한 2차곡선의 데이터셋은 다음과 같은 형태를 가진다.
plt.plot(X,y, "b.")
plt.show()
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(max_depth=2)
tree_reg1.fit(X,y)
DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
첫번째 예측기에서 생긴 잔여 오차(y2)에 두번째 예측기를 훈련시킨다.
y2 = y-tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg2.fit(X,y2)
DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=42, splitter='best')
마찬가지로 두번째 예측기가 만든 잔여 오차에 세번째 예측기를 훈련
y3 = y2-tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg3.fit(X,y3)
DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=42, splitter='best')
이제 세개의 트리를 포함하는 앙상블 모델을 만들었으니, 새로운 샘플에 대한 예측을 만들려면 모든 트리의 예측을 더하면 된다.
X_new = np.array([[0.8]]) # 새로운 샘플 0.8
y_pred = sum(tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3))
y_pred
array([0.75026781])
이렇게 구한 개별 예측기와 앙상블 모델에 대해 시각화를 해보자.
def plot_predictions(regressors, X, y, axes, label=None, style="r-", data_style="b.", data_label=None):
x1 = np.linspace(axes[0], axes[1], 500)
y_pred = sum(regressor.predict(x1.reshape(-1, 1)) for regressor in regressors)
plt.plot(X[:, 0], y, data_style, label=data_label)
plt.plot(x1, y_pred, style, linewidth=2, label=label)
if label or data_label:
plt.legend(loc="upper center", fontsize=16)
plt.axis(axes)
plt.figure(figsize=(11,11))
plt.subplot(321)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h_1(x_1)$", style="g-", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Residuals and tree predictions", fontsize=16)
plt.subplot(322)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1)$", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Ensemble predictions", fontsize=16)
plt.subplot(323)
plot_predictions([tree_reg2], X, y2, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_2(x_1)$", style="g-", data_style="k+", data_label="Residuals")
plt.ylabel("$y - h_1(x_1)$", fontsize=16)
plt.subplot(324)
plot_predictions([tree_reg1, tree_reg2], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1)$")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.subplot(325)
plot_predictions([tree_reg3], X, y3, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_3(x_1)$", style="g-", data_style="k+")
plt.ylabel("$y - h_1(x_1) - h_2(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)
plt.subplot(326)
plot_predictions([tree_reg1, tree_reg2, tree_reg3], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1)$")
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.show()
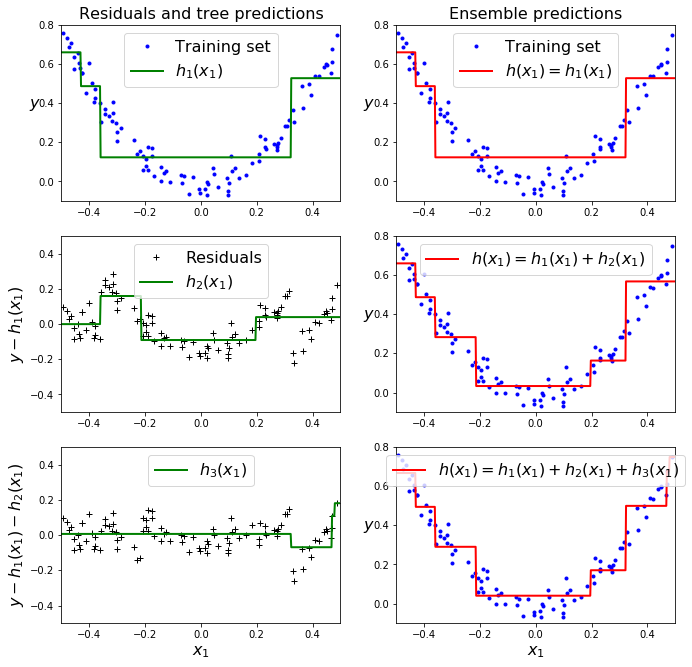
왼쪽열은 세개의 트리에 대한 개별 예측이고, 오른쪽열은 각각의 예측기의 잔여오차로 재학습하여 예측값을 더한 앙상블모델이다.
결정트리를 회귀문제에 이용할때는 예측값을 특정 구간에 대한 평균값을 이용하므로 계단형태를 띈다고 배웠었다(결정트리 포스팅).
첫번째 행은 하나의 예측기만 시행되었기 때문에 두그래프가 같고, 두번째 행은 첫번째 예측기의 잔여오차에 대해 학습되어 오른쪽의 앙상블 예측이 두개 예측의 합을 나타낸다.
세번째도 마찬가지다.
이렇게 트리가 앙상블에 추가될수록 예측이 점점 더 좋아지는 것을 볼 수 있다.
이러한 과정을 그래디언트 부스티드 회귀트리(Gradient Boosted Regression Tree, GBRT) 라고 한다.
사이킷런의 GradientBoostingRegressor를 사용하면 GBRT 앙상블을 간단하게 훈련시킬 수 있다.
from sklearn.ensemble import GradientBoostingRegressor
gbrt = GradientBoostingRegressor(max_depth=2,
n_estimators=3,
learning_rate=1.0,
random_state=42)
gbrt.fit(X,y)
GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None,
learning_rate=1.0, loss='ls', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=3,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
gbrt_slow = GradientBoostingRegressor(max_depth=2,
n_estimators=200,
learning_rate=0.1,
random_state=42)
gbrt_slow.fit(X, y)
GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None,
learning_rate=0.1, loss='ls', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=200,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
위 모델에 사용된 옵션(매개변수)은 다음과 같다.
n_estimators: 트리 수(즉, 반복 수)max_depth: 트리의 깊이(노드 수)learning_rate: 학습률
RandomForestRegressor와 같이 결정트리의 성장을 제어하는 매개변수와, 앙상블의 훈련을 제어하는 n_estimators 등을 제공한다.
learning_rate는 각 트리의 기여도를 조절하므로 0.1처럼 낮게 설정하면 앙상블을 훈련세트에 학습시키기위해 필요한 트리가 많아지지만 성능은 좋아진다.
다음은 같은 학습률, 다른 트리의 수로 예측한 GBRT앙상블 모델을 보여준다.
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_predictions([gbrt], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="Ensemble predictions")
plt.title("learning_rate={}, n_estimators={}".format(gbrt.learning_rate, gbrt.n_estimators), fontsize=14)
plt.subplot(122)
plot_predictions([gbrt_slow], X, y, axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("learning_rate={}, n_estimators={}".format(gbrt_slow.learning_rate, gbrt_slow.n_estimators), fontsize=14)
plt.show()
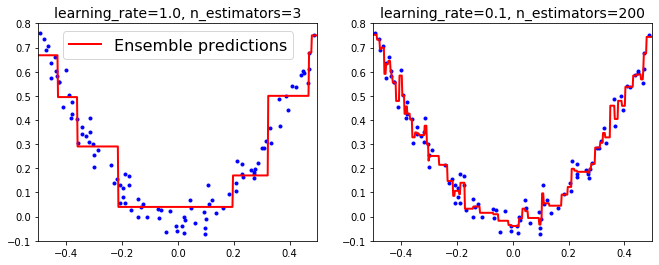
learning_rate을 1로했을때 왼쪽은 트리의 수가 너무 부족하고, 오른쪽은 너무 많아 과대적합된 경우이다.
이런 경우에 staged_predict()메서드를 사용해 최적의 트리 수를 구할 수 있다.
이는 훈련의 각 단계(트리가 1개일때, 2개일때,.. 등)에서 앙상블에 의해 만들어진 예측기를 순회하는 반복자(iterator)를 반환한다.
다음 코드는 120개의 트리로 GBRT앙상블을 훈련시키고 최적의 트리 수를 찾기위해 각 훈련단계에서 검증 오차를 측정하여 최적의 트리 수를 구하고 최종 GBRT 앙상블을 훈련시킨다.
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
X_train, X_val, y_train, y_val = train_test_split(X,y)
gbrt = GradientBoostingRegressor(max_depth=2,
n_estimators= 120)
gbrt.fit(X_train, y_train)
errors = [mean_squared_error(y_val, y_pred)
for y_pred in gbrt.staged_predict(X_val)]
bst_n_estimators = np.argmin(errors) + 1
# np.argim(array) : array에서 최솟값의 인덱스를 반환
# 즉, 최소값을 갖게하는 인덱스로 최적 트리의 수를 판단
gbrt_best = GradientBoostingRegressor(max_depth=2,
n_estimators=bst_n_estimators,
random_state=42)
gbrt_best.fit(X_train,y_train)
GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None,
learning_rate=0.1, loss='ls', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=63,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
이제 검증오차를 통해 최솟값을 찾은 것과, 최적의 트리 수를 찾아 훈련한 앙상블 모델을 시각화해보자.
min_error = np.min(errors)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(errors, "b.-")
plt.plot([bst_n_estimators, bst_n_estimators], [0, min_error], "k--")
# y 수직선 0~0.004 (x는 83위치)
plt.plot([0, 120], [min_error, min_error], "k--")
# x 수평선 0~120 (y는 min_error위치, 0.004)
plt.plot(bst_n_estimators, min_error, "ko")
plt.text(bst_n_estimators, min_error*1.2, "Minimum", ha="center", fontsize=14)
plt.axis([0, 120, 0, 0.01])
plt.xlabel("Number of trees")
plt.title("Validation error", fontsize=14)
plt.subplot(122)
plot_predictions([gbrt_best], X, y, axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("Best model (%d trees)" % bst_n_estimators, fontsize=14)
plt.show()
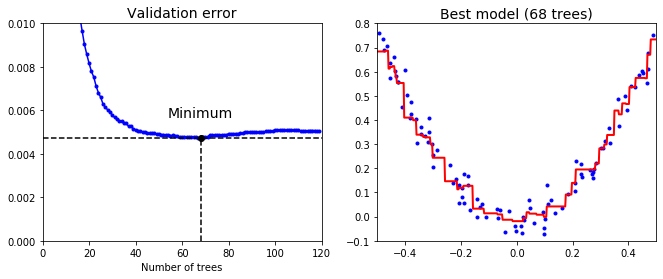
왼쪽은 검증 오차, 오른쪽은 최적 앙상블 모델의 예측이다.
이렇게 위와 같은 방법처럼 120개의 트리를 모두 훈련시키고 최적의 수를 찾기위해 검증오차를 분석하는 대신, 조기 종료를 이용할 수 있다.
warm_start=True로 설정하면 fit()메서드가 호출될 때 기존 트리를 유지하고 훈련을 추가할 수 있도록 해준다.
다음 코드는 연속해서 다섯번의 반복동안 검증오차가 향상되지 않으면 훈련을 멈추는 과정이다.
X_train, X_val, y_train, y_val = train_test_split(X,y)
gbrt = GradientBoostingRegressor(max_depth = 2,
warm_start=True, # 기존 트리를 유지
random_state=42)
min_val_error = float("inf")
error_going_up = 0
for n_estimators in range(1,120):
gbrt.n_estimators = n_estimators # 트리 수 입력
gbrt.fit(X_train, y_train) # 훈련
y_pred = gbrt.predict(X_val) # 예측값 생성
val_error = mean_squared_error(y_val, y_pred) # MSE 계산
if val_error < min_val_error: # 초기 min_val_error는 무한대(inf)
min_val_error = val_error
error_going_up = 0
else:
error_going_up += 1 # 누적
if error_going_up == 5: # 연속해서 5번이나 MSE가 기존보다 크면
break # 조기 종료
print("최적의 트리 수 :", n_estimators)
print("최적일 때의 MSE :", min_val_error)
최적의 트리 수 : 58
최적일 때의 MSE : 0.003316708108907353
앙상블 모델 초기에는 n_estimators 매개변수를 지정하지 않고, 1개부터 차례로 지정해가며 fit()을 호출한다.
그 후, MSE가 이전 MSE보다 크게나온 경우가 연속해서 5번이 될 경우 훈련을 멈춘다.
그리고 GradientBoostingRegressor는 각 트리가 훈련할 때 사용할 훈련 샘플의 비율을 subsample옵션으로 지정할 수 있다.
예를들어 subsample=0.25라고 지정하면 트리는 무작위로 선택된 25%의 훈련 샘플로 학습된다.
이렇게하면 편향은 높아지지만(과소적합위험 증가) 분산이 낮아지고(과대적합위험 감소) 훈련속도를 상당히 높일 수 있다.
이런 기법을 확률적 그래디언트 부스팅(Stochastic Gradient Boosting) 이라고 한다.
또한 loss옵션을 통해 비용함수를 지정해 줄 수 있다.
GradientBoostingClassifier의 default는devianceGradientBoostingRegressor의 default는ls(최소제곱)
3. XGBosst
XGBoost 내용 추가예정
X_train, X_val, y_train, y_val = train_test_split(X,y)
import xgboost
xgb_reg = xgboost.XGBRegressor(random_state=42)
xgb_reg.fit(X_train, y_train)
y_pred = xgb_reg.predict(X_val)
val_error = mean_squared_error(y_val, y_pred)
print("Validation MSE:", val_error)
[00:33:03] WARNING: C:/Jenkins/workspace/xgboost-win64_release_0.90/src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
Validation MSE: 0.004181325440984155
xgb_reg.fit(X_train, y_train,
eval_set=[(X_val, y_val)], early_stopping_rounds=2)
y_pred = xgb_reg.predict(X_val)
val_error = mean_squared_error(y_val, y_pred)
print("Validation MSE:", val_error)
[00:33:26] WARNING: C:/Jenkins/workspace/xgboost-win64_release_0.90/src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
[0] validation_0-rmse:0.296481
Will train until validation_0-rmse hasn't improved in 2 rounds.
[1] validation_0-rmse:0.270065
[2] validation_0-rmse:0.24498
[3] validation_0-rmse:0.22376
[4] validation_0-rmse:0.205112
[5] validation_0-rmse:0.187807
[6] validation_0-rmse:0.172791
[7] validation_0-rmse:0.157777
[8] validation_0-rmse:0.144445
[9] validation_0-rmse:0.133176
[10] validation_0-rmse:0.122882
[11] validation_0-rmse:0.114259
[12] validation_0-rmse:0.106627
[13] validation_0-rmse:0.099981
[14] validation_0-rmse:0.094226
[15] validation_0-rmse:0.089749
[16] validation_0-rmse:0.085981
[17] validation_0-rmse:0.0825
[18] validation_0-rmse:0.079568
[19] validation_0-rmse:0.076426
[20] validation_0-rmse:0.074301
[21] validation_0-rmse:0.072217
[22] validation_0-rmse:0.070208
[23] validation_0-rmse:0.06914
[24] validation_0-rmse:0.067514
[25] validation_0-rmse:0.066792
[26] validation_0-rmse:0.06643
[27] validation_0-rmse:0.06537
[28] validation_0-rmse:0.064468
[29] validation_0-rmse:0.064292
[30] validation_0-rmse:0.064095
[31] validation_0-rmse:0.063506
[32] validation_0-rmse:0.063709
[33] validation_0-rmse:0.063634
Stopping. Best iteration:
[31] validation_0-rmse:0.063506
Validation MSE: 0.004032999596648908
%timeit xgboost.XGBRegressor().fit(X_train, y_train)
32.4 ms ± 1.07 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
%timeit GradientBoostingRegressor().fit(X_train, y_train)
15.7 ms ± 291 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
XGboost와 관련 내용은 별도의 포스팅으로 추후에 업로드 할 예정이다.
스태킹(Stacking)
지금까지는 앙상블에 속하는 모든 예측기의 예측을 취합하는 방식에 대한 여러가지 방법론을 다뤘다.
하지만 스태킹(stacking)은 취합하는 모델자체를 훈련시키고자 하는 것에서 시작된다.
이것은 사이킷런에서 제공하지 않으므로 간단하게만 알아보자.
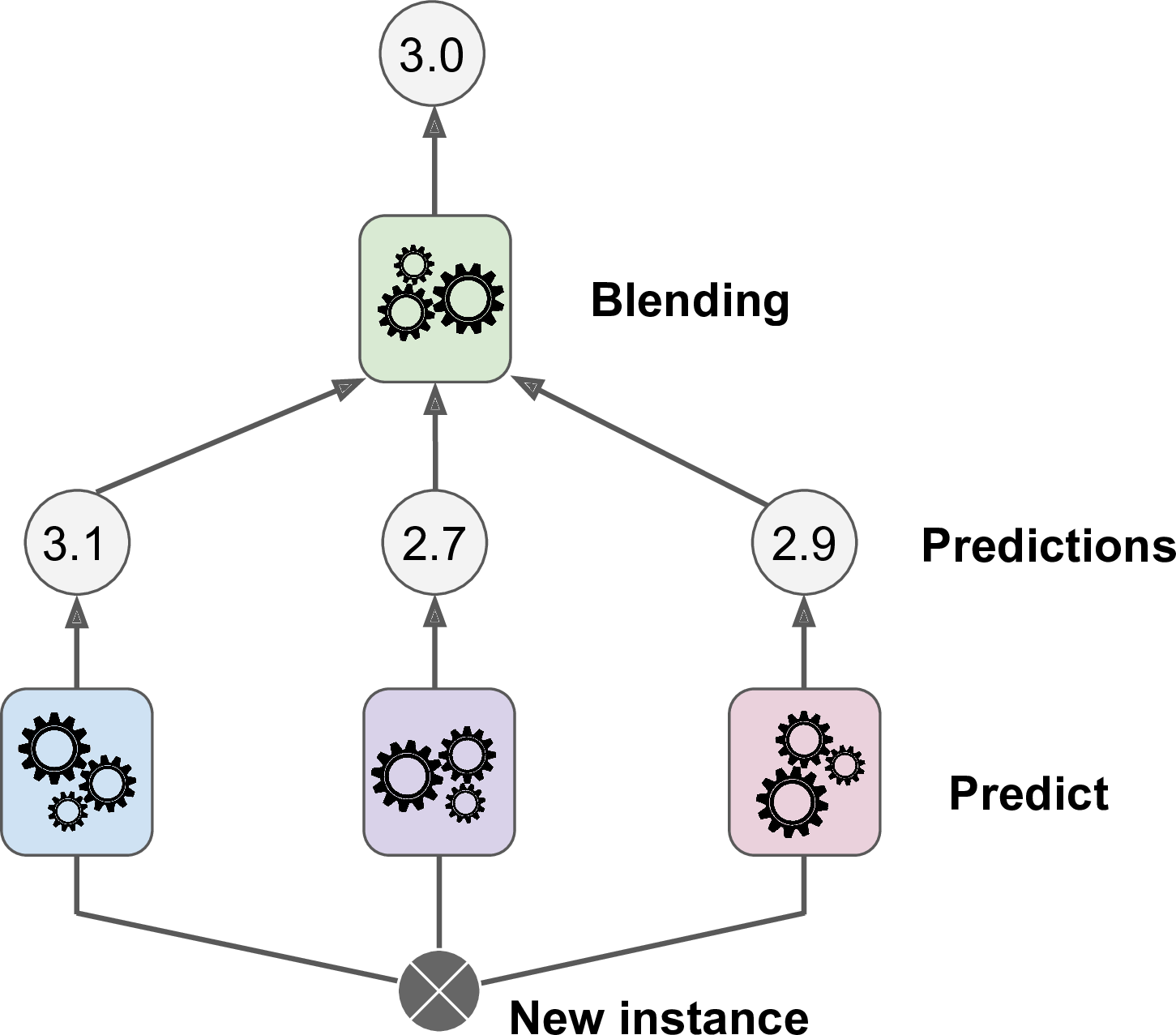
위 그림은 훈련된 3개의 예측기가 새로운 샘플에 대해 각 예측값을 반환했고, 블렌더(Blender) 또는 메타 학습기(meta learner)라는 마지막 예측기가 3개의 예측을 학습해 최종 예측값 3.0을 반환하는 것을 보여준다.
일반적 방법으로 홀드 아웃(hold-out) 세트를 사용하는데, 그 과정을 살펴보자.
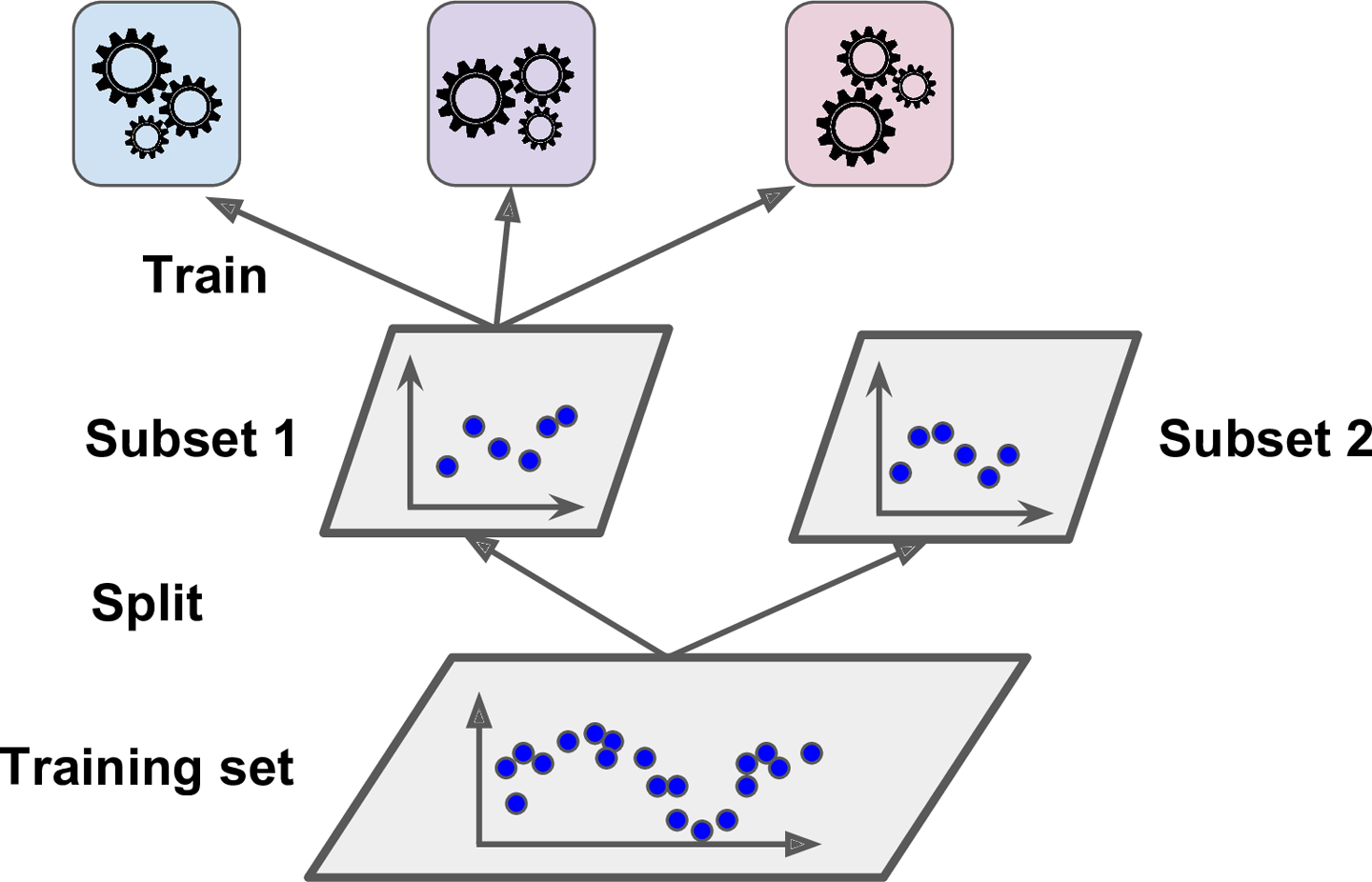
- 먼저 training set을 2개의 subset으로 나눈다.
- subset1은 첫번째 레이어의 예측기들을 훈련시키는데 사용
- 훈련된 첫번째 레이어의 예측기로 subset2에 대한 예측을 생성
(subset이지만 훈련에 사용이 안됐으므로 test셋처럼 사용 가능)
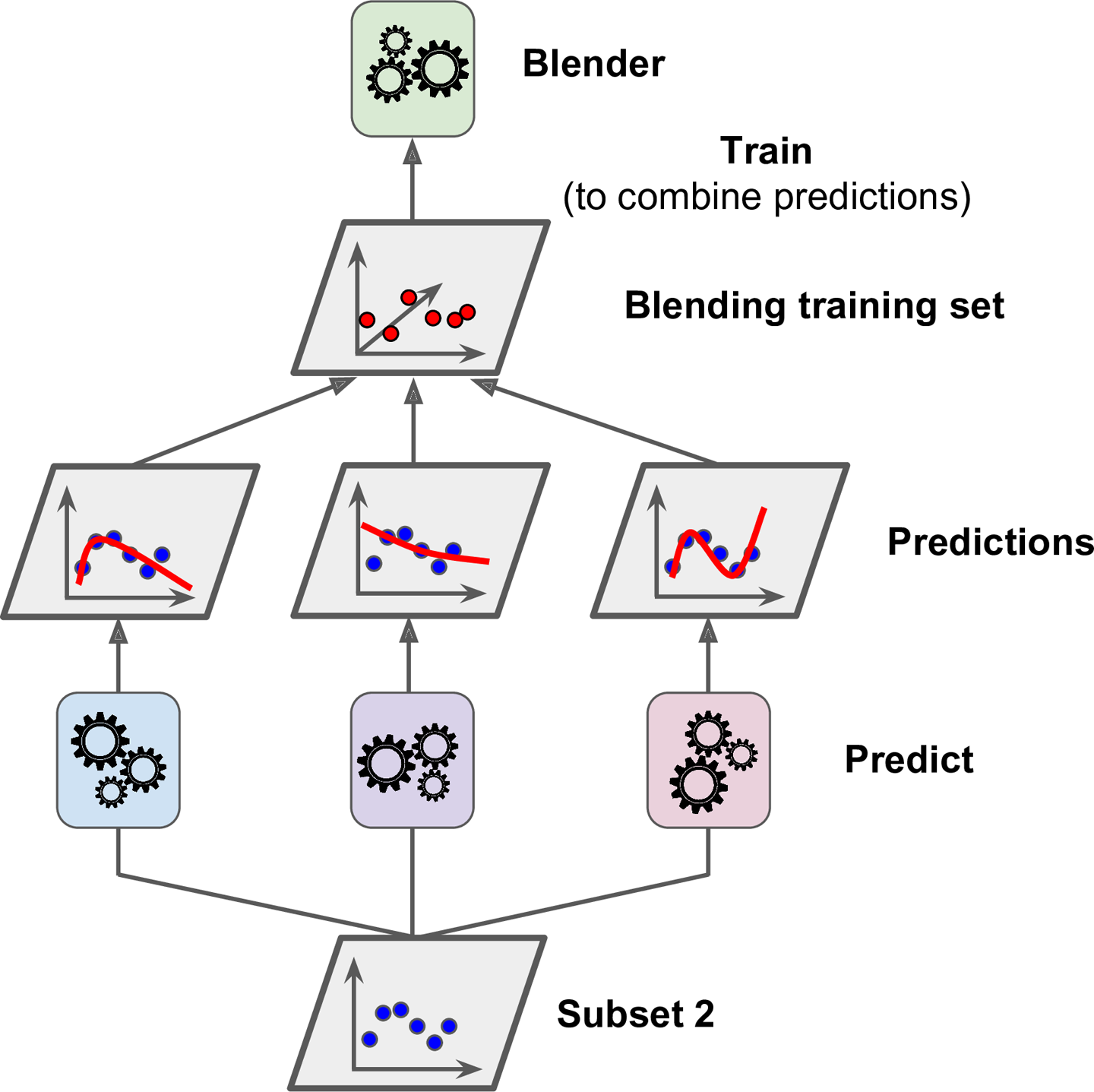
- 세개의 예측값 생성
- 타깃값(y)은 그대로 쓰고 앞에서 예측한 3개의 값(y_hat)을 입력 변수로 사용하는 새로운 훈련세트 생성
(즉, 새로운 훈련세트는 3차원이 된다) - 블렌더가 새로운 훈련 세트로 학습
(즉, 첫번째 레이어의 예측 3개를 이용해 y를 예측하도록 학습되는 것이다.)
이런 방식으로 블렌더를 여러개 훈련 시키는 것도 가능하다(하나는 선형회귀, 하나는 랜덤포레스트 등등..)
그러면 블렌더만의 레이어가 또 만들어지게 된다. 이 경우는 그러면 애초에 subset을 3개까지 나누어야 한다.
즉, subset1은 첫번째 레이어의 예측기들을 훈련시키고,
subset2로 첫번째 예측기들의 예측을 만들어 블렌더 레이어의 예측기를 위한 훈련세트를 생성하고,
subset3로 두번째 예측기들의 예측을 만들어 세번째 레이어를 훈련시키기 위한 훈련세트를 만드는데 사용된다.
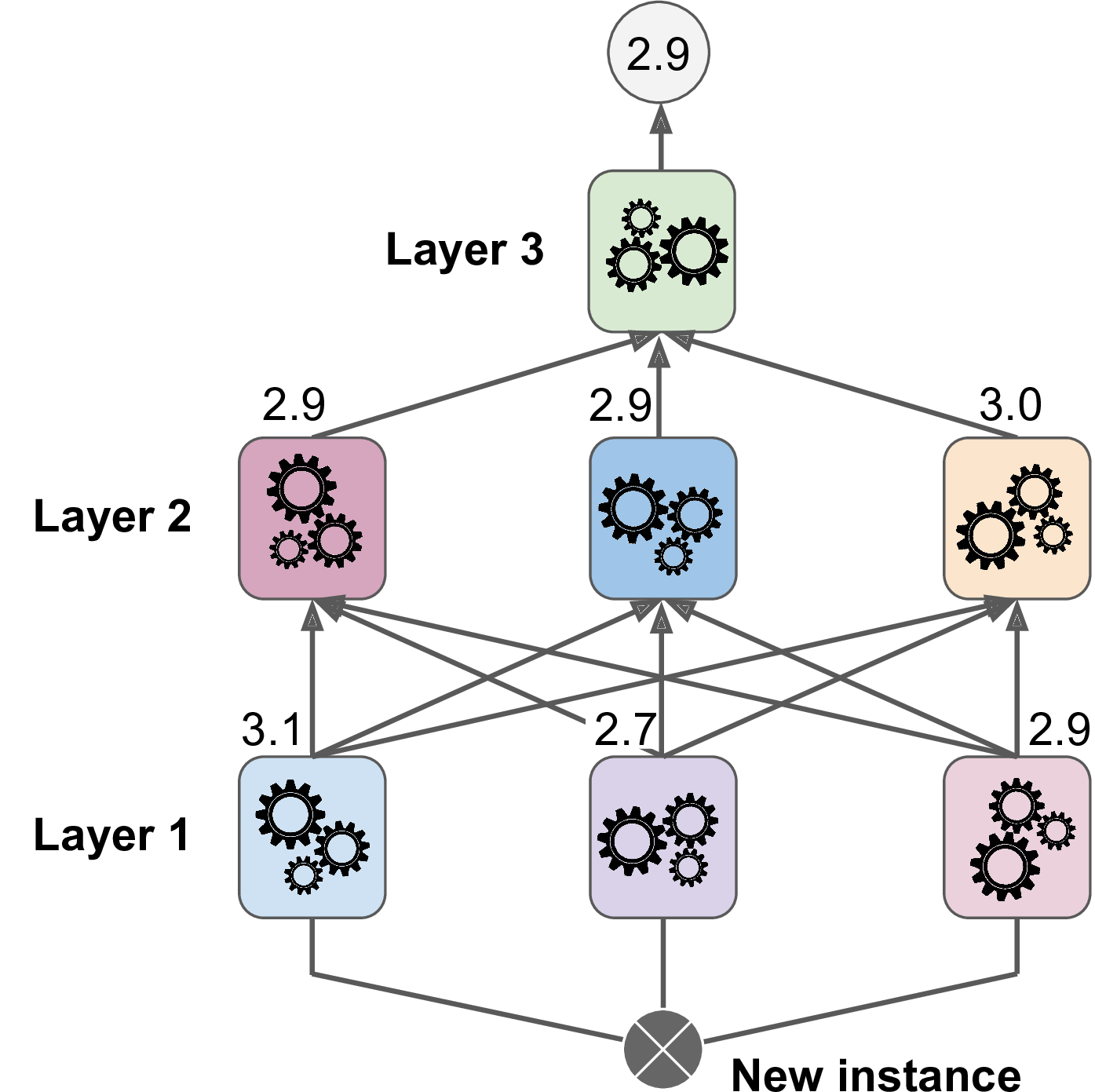
이 작업들이 끝나면, 위 그림 처럼 차례대로 실행해서 새로운 샘플에 대한 예측을 만들 수 있다.
직접 구현하는 것도 어렵지는 않고, brew같은 오픈소스를 이용할 수 있다.
(참조 : http://github.com/viisar/brew)
Reference
도서 [Hands-0n Machine Learning with Scikit-Learn & Tensorflow] 를 공부하며 작성하였습니다.




댓글남기기