[Handson ML] 릿지(Ridge),라쏘(Lasso),엘라스틱 넷(Elsatic-net) - 모델 훈련
업데이트:
개요

모델의 과대적합을 방지하는 좋은 방법은 모델에 규제를 가하는 방법이다.
이러한 방법으로 다항회귀모델의 다항식 차수를 감소시키는 등 자유도를 줄이는 방법이 있다.
보통 선형회귀모델에서는 모델의 가중치를 제한함으로써 규제를 가하는데, 이번 포스팅에서는 이러한 가중치를 제한하는 릿지, 라쏘, 엘라스틱넷에 대해 공부해보도록 하자.
1. 릿지 회귀
릿지 회귀(Ridge Regression)는 통계학에서 능형회귀라고 부르는데, 선형회귀에 규제가 추가된 것으로 비용함수에 다음 항이 추가된다.
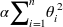
이 규제는 비용함수에 추가되는 것으로 테스트 세트에서 성능을 평가하거나 실제 샘플을 예측할때는 적용되지 않는다.
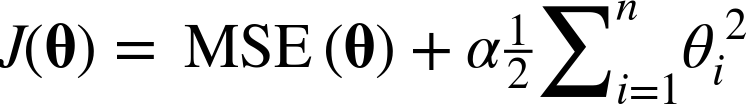
위 식의 하이퍼파라미터인 α는 모델을 얼마나 많이 규제할지 조절한다.
α=0이면 릿지회귀는 선형회귀와 같아지고, α가 커질수록 모든 가중치가 0에 가까워져 결국 데이터의 평균을 지나는 수평선이 된다.
위 식에서 i가 1부터 시작하는 것은 θ0는 규제되지 않는 것을 의미한다.
w를 가중치 벡터(θ1~θn)라고 정의하면 규제항은 ½(∥ w ∥2)^2와 같다.
(½을 곱한 것은 미분하면 2를 곱해 깔끔하게 떨어지게 하기 위함)
여기서 ∥ w ∥2가 가중치 벡터의 ℓ2노름이다.
이를 경사하강법에 적용하려면 MSE 그라디언트 벡터에 αw를 더하면 된다.
(참고 : 경사하강법)
선형회귀와 마찬가지로 릿지 회귀를 계산하기 위해 정규방정식과 경사하강법을 이용할 수 있다(이 두 계산방식의 장단점은 선형회귀 포스팅의 계산복잡도에 관련이 있다).
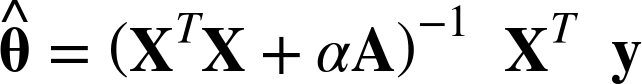
위 식은 릿지회귀의 정규방정식으로, A는 편향에 해당하는 맨 왼쪽 위의 원소가 0인 (n+1)X(n+1)의 단위 행렬이다.
(원래 단위 행렬은 주대각선이 1이지만, 편향에 해당하는 θ0는 규제에 포함되지 않으기 때문)
선형 데이터 셋에 정규방정식을 사용하여 릿지모델을 훈련시켜보자.
import numpy as np
np.random.seed(42)
m = 20 # 데이터 수
X = 3 * np.random.rand(m, 1) # 0~1 난수*3
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5 # 1차방정식 형태
X_new = np.linspace(0, 3, 100).reshape(100, 1) # 0~3사이 100개
solver="cholesky"를 사용하면 숄레스키 분해라고도 하는 행렬분해를 이용해 정규방정식의 해를 구하는데 유용하다.
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1,
solver="cholesky",
random_state=42)
ridge_reg.fit(X,y)
ridge_reg.predict([[1.5]]) # 새로운 샘플에 대한 예측
array([[1.55071465]])
이번엔 경사하강법을 이용해 릿지모델을 훈련시켜보자.
이전 포스팅에서도 배웠지만, 정규방정식의 해를 구하기 위해 역행렬을 계산하는 과정에서 시간이 매우 오래걸리므로, 경사하강법이 유용할 때가 있다.
solver='sag'를 이용하면 확률적 평균 경사하강법(Stochastic Average Gradient Descent)를 사용할 수 있다.
이는 SGD와 비슷하지만 현재 gradient와 이전 단계에서 구한 모든 gradient를 합해서 평균한 값으로 모델 파라미터를 갱신한다.
ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
array([[1.5507201]])
SGDRegressor을 이용한 방법이다.
penalty옵션으로 사용할 규제를 지정하는데 “l2”는 SGD가 비용함수에 가중치 벡터의 ℓ2노름의 제곱을 2로 나눈 규제항을 추가하게 만든다(즉, 릿지 회귀가 된다.).
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=5,
penalty="l2",
random_state=42)
sgd_reg.fit(X,y.ravel())
sgd_reg.predict([[1.5]])
array([1.13500145])
다음은 각기다른 α를 사용해 릿지모델을 훈련시킨 결과이다.
왼쪽은 평병한 릿지모델, 오른쪽은 다항회귀(PolynomialFeatures(degree=10))를 사용해 먼저 데이터를 확장하고 StandardScaler를 사용해 스케일 조정 후 릿지모델에 적용한 결과이다.
(규제를 사용한 다항회귀)
from sklearn.linear_model import Ridge, LinearRegression
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
def plot_model(model_class, polynomial, alphas, **model_kargs):
for alpha, style in zip(alphas, ("b-", "g--", "r:")):
model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()
if polynomial:
model = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("std_scaler", StandardScaler()),
("regul_reg", model),
])
model.fit(X, y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left", fontsize=15)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 3, 0, 4])
plt.figure(figsize=(10,4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)
plt.show()
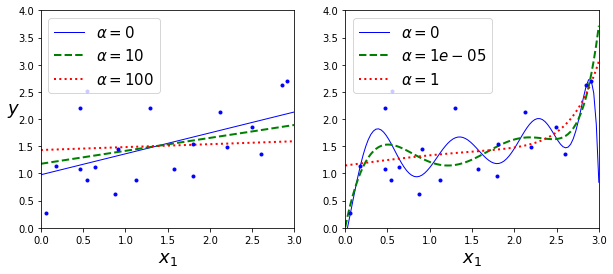
α를 증가시킬수록 직선에 가까워 지는 것을 알 수 있다(분산은 줄고 편향이 증가).
2. 라쏘 회귀
라쏘 회귀(Lasso Regression) 는 릿지 회귀처럼 비용함수에 규제항을 더하지만 ℓ2노름의 제곱을 2로 나눈 것 대신 가중치 벡터의 ℓ1노름을 사용한다.
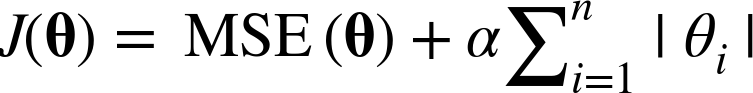
다음은 위와 같은 방법으로 릿지 대신 라쏘모델과 더 작은 α를 사용한 결과이다.
from sklearn.linear_model import Lasso
plt.figure(figsize=(10,4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)
plt.show()
c:\users\user\appdata\local\programs\python\python37\lib\site-packages\sklearn\linear_model\coordinate_descent.py:475: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Duality gap: 2.802867703827423, tolerance: 0.0009294783355207351
positive)
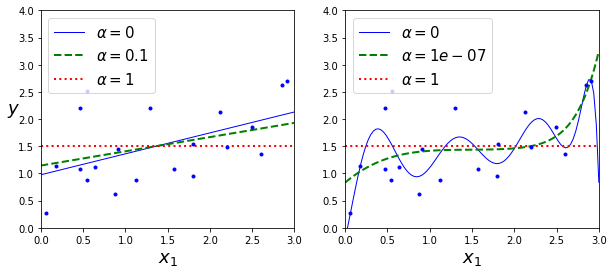
라쏘회귀의 중요한 특징은 덜 중요한 변수의 가중치를 완전히 제거하려고 한다는 점이다.
위 그래프를 보면 다항회귀의 차수가 거의 0이 되어가는(직선이 되어가는) 것을 볼 수 있다.
즉, 라쏘회귀는 자동으로 변수를 선택하고 희소모델(sparse model)을 만든다(즉, 0이아닌 변수의 가중치가 적다).
다음은 다차원 방정식 y = 2x1 + 0.5x2로, 최적의 파라미터는 θ1=2, θ2=0.5이다.
t1a, t1b, t2a, t2b = -1, 3, -1.5, 1.5
t1s = np.linspace(t1a, t1b, 500)
t2s = np.linspace(t2a, t2b, 500)
t1, t2 = np.meshgrid(t1s, t2s)
T = np.c_[t1.ravel(), t2.ravel()]
Xr = np.array([[1, 1], [1, -1], [1, 0.5]])
yr = 2 * Xr[:, :1] + 0.5 * Xr[:, 1:]
J = (1/len(Xr) * np.sum((T.dot(Xr.T) - yr.T)**2, axis=1)).reshape(t1.shape)
N1 = np.linalg.norm(T, ord=1, axis=1).reshape(t1.shape)
N2 = np.linalg.norm(T, ord=2, axis=1).reshape(t1.shape)
t_min_idx = np.unravel_index(np.argmin(J), J.shape)
t1_min, t2_min = t1[t_min_idx], t2[t_min_idx]
t_init = np.array([[0.25], [-1]])
def bgd_path(theta, X, y, l1, l2, core = 1, eta = 0.05, n_iterations = 200):
path = [theta]
for iteration in range(n_iterations):
gradients = core * 2/len(X) * X.T.dot(X.dot(theta) - y) + l1 * np.sign(theta) + l2 * theta
theta = theta - eta * gradients
path.append(theta)
return np.array(path)
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10.1, 8))
for i, N, l1, l2, title in ((0, N1, 2., 0, "Lasso"), (1, N2, 0, 2., "Ridge")):
JR = J + l1 * N1 + l2 * 0.5 * N2**2
tr_min_idx = np.unravel_index(np.argmin(JR), JR.shape)
t1r_min, t2r_min = t1[tr_min_idx], t2[tr_min_idx]
levelsJ=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J)
levelsJR=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR)
levelsN=np.linspace(0, np.max(N), 10)
path_J = bgd_path(t_init, Xr, yr, l1=0, l2=0)
path_JR = bgd_path(t_init, Xr, yr, l1, l2)
path_N = bgd_path(np.array([[2.0], [0.5]]), Xr, yr, np.sign(l1)/3, np.sign(l2), core=0)
ax = axes[i, 0]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, N / 2., levels=levelsN)
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.set_title(r"$\ell_{}$ penalty".format(i + 1), fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
ax.set_ylabel(r"$\theta_2$", fontsize=16, rotation=0)
ax = axes[i, 1]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, JR, levels=levelsJR, alpha=0.9)
ax.plot(path_JR[:, 0], path_JR[:, 1], "w-o")
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.plot(t1r_min, t2r_min, "rs")
ax.set_title(title, fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
plt.show()
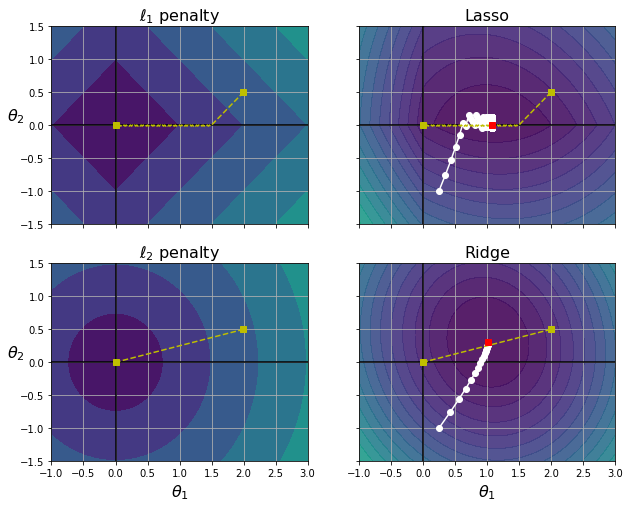
MSE 비용함수는 동일하지만, ℓ1,ℓ2 페널티 그래프에 있는 등고선은 다르다(왼쪽 열).
오른쪽 열은 비용함수에 규제항이 포함되어 있어서(라쏘와 릿지) 등고선이 다르게 나타나며초 최적 파라미터 값(빨간 네모)이 달라진 것을 볼 수 있다.
라쏘 비용함수에서 배치 경사하강법의 경로가 전역 최솟값(빨간 네모)으로 가는 도중에 지그재그로 튀는 경향을 보이는데, 이는 θ2=0에서 기울기가 갑자기 바뀌기 때문이다.
라쏘의 비용함수가 θi=0에서 미분가능하지 않기 때문인데, 이를 위해 서브그래디언트 벡터 g(미분이 불가능한 지점 근방 그래디언트들의 중간값)를 사용할 수 있다.
공식은 다음과 같다(경사하강법 적용을 위해 라쏘 비용함수에 사용할 수 있는 서브그래디언트 공식).
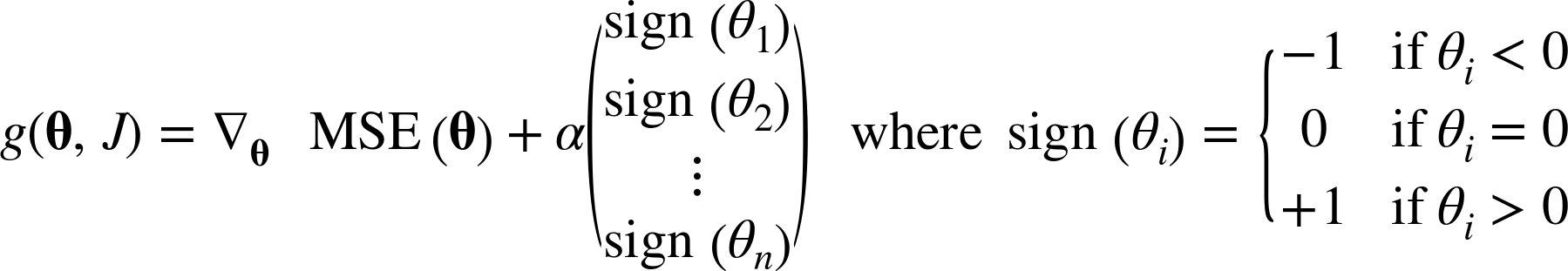
전역 최솟값에 수렴하기 위해서 학습률을 점진적으로 줄여나갈 필요가 있다.
위 그래프에 대해 완벽하게 이해가 되지 않아서, 여기1와 여기2에 들어가보면 자세하고 명확한 설명이 나와있으니 참고하면 좋을 것 같다.
다음은 사이킷런의 Lasso모듈을 사용한 예제이다.
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha = 0.1)
lasso_reg.fit(X,y)
lasso_reg.predict([[1.5]])
array([1.53788174])
마찬가지로 SGDRegressor(penalty='l1')을 사용할 수도 있다.
3. 엘라스틱넷
엘라스틱 넷(Elastic Net)은 릿지회귀와 라쏘회귀를 절충한 모델이다.
규제항은 릿지와 회귀의 규제항을 단순히 더해서 사용하며, 두 규제항의 혼합정도를 혼합비율 r을 사용해 조절한다.
r=0이면 릿지회귀와 같고, r=1이면 라쏘회귀와 같다.
식은 다음과 같다.
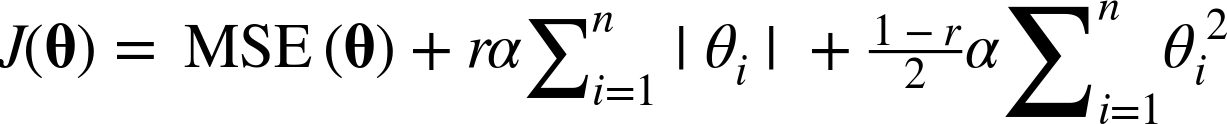
그렇다면 지금까지 배운 규제가 있거나 없는 선형모델들을 언제 사용해야 할까?
적어도 규제가 있는 것이 없는 것보다는 대부분의 경우에 좋고, 릿지가 기본이 되지만 실제로 쓰이는 변수가 몇 개뿐이라고 의심되면 라쏘나 엘라스틱넷을 이용하자(라쏘는 덜 중요한 변수의 가중치를 0으로 만들어버려 변수선택의 효과가 있다).
하지만 극단적으로 변수의 수가 훈련샘플의 수 보다도 많고, 변수 몇개가 강하게 연관(다중공선성 의심)되어 있을 경우에는 라쏘에 문제가 발생하므로 엘라스틱넷을 선호한다.
라쏘는 변수 수가 샘플 수(n)보다 많으면 최대 n개의 변수를 선택하고, 여러 변수간 강한 상관관계를 띄면 임의의 변수 하나를 선택한다.
다음은 ElasticNet을 사용한 간단한 예제이다.
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
array([1.54333232])
4. 조기 종료
조기종료란 경사하강법과 같이 반복학습 알고리즘을 규제하는 방법으로, 검증 에러가 최솟값에 도달하면 훈련을 중지(조기 종료)시키는 것이다.
다음은 배치 경사하강법으로 훈련시킨 복잡한 모델(고차원 다항회귀모델)을 보여준다.
# 비선형 데이터 생성
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)
plt.plot(X,y,"b.")
plt.show()
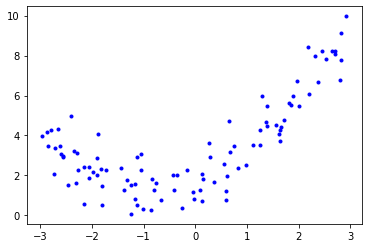
이제 이 데이터를 이용해 조기종료할 시점이 어디일지 찾아보자.
from sklearn.model_selection import train_test_split
# 훈련, 검증 데이터 셋 생성
X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(),
test_size=0.5,
random_state=10)
from sklearn.base import clone
from sklearn.metrics import mean_squared_error
# 90차 다항회귀모델 및 스케일 조정
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler())
])
# 훈련, 검증 세트로 고차원 다항회귀모델을 통해 새로운 변수 추가(90개)
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
# SGD모델 생성
sgd_reg = SGDRegressor(max_iter=1,
tol=-np.infty,
warm_start=True, # fit()메서드 호출마다 기존 유지
penalty=None,
learning_rate="constant",
eta0=0.0005,
random_state=42)
# 초기 검증오차 무한대로 지정
minimum_val_error = float("inf")
best_epoch = None
best_model = None
# 1000번의 epoch 실행
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # 연속적인 fit메서드 호출
y_val_predict = sgd_reg.predict(X_val_poly_scaled) # 검증 세트 훈련
val_error = mean_squared_error(y_val, y_val_predict) # 검증 세트 평가
# 검증 오차를 계속 비교해가면서 최적 단계와 모델 찾기
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
print("최적 step :", best_epoch)
최적 step : 239
warm_strat=True옵션을 주면 fit()메서드가 호출될 때 알고리즘이 처음부터 다시 학습하지 않고, 이전 모델 파라미터에서 훈련을 이어가도록 할 수 있다.
239번째 epoch에서 가장 작은 검증오차를 보여, 그 후로 학습이 진행되더라도 검증오차가 이보다 작아지지 않기 때문에 이 단계에서의 조기종료가 필요할 것으로 예상된다.
시각화해보자.
sgd_reg = SGDRegressor(max_iter=1,
tol=-np.infty,
warm_start=True,
penalty=None,
learning_rate="constant",
eta0=0.0005,
random_state=42)
n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
sgd_reg.fit(X_train_poly_scaled, y_train)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
train_errors.append(mean_squared_error(y_train, y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])
plt.annotate('Best model',
xy=(best_epoch, best_val_rmse),
xytext=(best_epoch, best_val_rmse + 1),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.05),
fontsize=16,
)
best_val_rmse -= 0.03 # 좀 더 보기좋게 표시하기 위함
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set")
plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Epoch", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
plt.show()
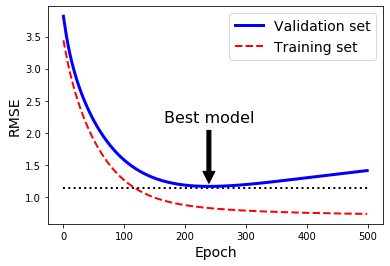
그래프를 보면 검증세트(Validation Set)는 알고리즘이 학습됨에 따라 RMSE는 감소하면서 최솟값에 도달했다가 다시 상승하는 것을 알 수 있다.
이는 모델이 훈련데이터에 과대적합되었기 때문에 나타나는 현상이다.
SGD나 미니배치 경사하강법의 경우 비용함수의 곡선이 매끄럽지 않아서 최솟값에 도달했는지 확인하기 어려울 수 있다.
이럴때, 검증 오차가 일정 시간동안(일정 횟수동안) 최솟값보다 클 때 모델이 더 개선되지 않는다고 판단하여 학습을 멈추고 최소였던 검증오차로 되돌아가는 방식을 사용할 수 있다.
Reference
도서 [Hands-0n Machine Learning with Scikit-Learn & Tensorflow] 를 공부하며 작성하였습니다.




댓글남기기