[Handson ML] 다항회귀(Polynomial Regression) - 모델 훈련

개요

다항 회귀(Polynomial Regression)는 비선형 데이터를 학습하기 위해 선형모델을 사용하는 기법으로, 각 변수의 거듭제곱을 새로운 변수로 추가하고 이 확장된 변수를 포함한 데이터셋에 선형모델을 훈련시킨다.

다항회귀

간단한 예로 2차방정식으로 비선형데이터를 생성해보자.

import numpy as np
import matplotlib.pyplot as plt

m = 100
X = 6 * np.random.rand(m,1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m,1)  # 약간의 노이즈 포함

plt.plot(X,y,"b.")
plt.ylabel("Y", fontsize=15,rotation=0)
plt.xlabel("X", fontsize=15)
plt.show()

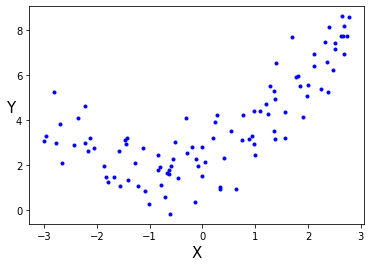
이렇게 비선형적으로 분포하고 있는 데이터에 단순히 직선으로 예측하는 것은 잘 안맞을 것이다.

사이킷런의 PolynomialFeatures를 사용해보자.

from sklearn.preprocessing import PolynomialFeatures

poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)

print(X[0])
print(X_poly[0])

[2.10576397]
[2.10576397 4.43424189]

파라미터 degree=2는 2차다항을 생성한다는 것이고, include_bias=False는 default가 True인데 True이면 편향을 위한 변수(X0)인 1이 추가된다.

이와 같이 각 변수(X)값들을 제곱하여(degree=2), 새로운 변수를 만들어 주는 역할을 한다.

이제 이 확장된 훈련데이터(변수가 2개가 됨)에 LinearRegression을 적용해보자.

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_ , lin_reg.coef_

(array([2.24688621]), array([[0.8519921 , 0.47311237]]))

X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
plt.show()

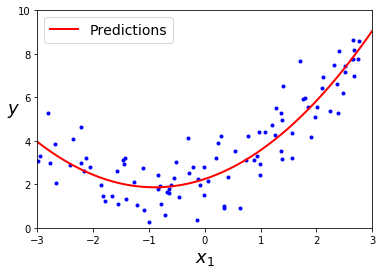
맨 처음에 설정했었던 원래 함수가 y = 0.5 * X**2 + X + 2 + 가우시안 노이즈이고 예측모델은 위와 같으니 나쁘진 않다.

변수가 여러개 일때 다항회귀는 이 변수사이의 관계를 찾을 수도 있다.
PolynomialFeatures가 주어진 파라미터(degree)까지 변수 간 모든 교차항을 추가하기 때문이다.

예를들어 두 개의 독립변수 a,b가 있을때 degree=3을 주면, a^2,a^3,b^2,b^3에다가 ab,a^2b,ab^2까지 변수로 추가한다.

즉, PolynomialFeatures(degree=d)는 변수가 n개인 배열의 변수를 (n+d)! / d!n!개의 변수 배열로 반환하므로, 너무 늘어나지 않도록 주의해야한다.

참고로 interection_only=True로 지정하면 거듭제곱이 포항된 항은 제외된다.
(즉, 거듭제곱이 있는 항 빼고 a,b,ab만 남는다.)
get_feature_names()를 사용하면 만들어진 변수의 차수를 쉽게 확인이 가능하다.

학습곡선

다항 회귀의 차수(degree)가 높아질수록 더 훈련데이터에 fitting을 시도할 것이다.(과대적합이 일어남)

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

for style, width, degree in (("g-", 1, 300), ("b--", 2, 2), ("r-+", 2, 1)):
    polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
    std_scaler = StandardScaler()
    lin_reg = LinearRegression()
    polynomial_regression = Pipeline([
            ("poly_features", polybig_features),
            ("std_scaler", std_scaler),
            ("lin_reg", lin_reg),
        ])
    polynomial_regression.fit(X, y)
    y_newbig = polynomial_regression.predict(X_new)
    plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)

plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()

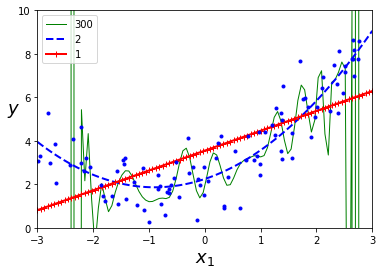
위 그림은 1차(직선), 2차, 300차 다항 회귀모델을 훈련데이터에 적합한 결과이다.

애초에 훈련데이터가 2차방정식으로 생성되었기 때문에, 당연한 결과(2차 다항이 잘맞음)이지만, 일반적 상황에서는 degree를 어떻게 주어야 할까?

앞에서 cross_val_score등을 이용해 교차검증을 시행한 방법도 있지만, 여기서는 훈련 셋과 검증 셋의 모델 성능을 훈련 셋의 크기 함수로 나타내는 학습곡선을 활용해보자.

이를 위해서는 훈련 데이터 셋을 크기가 다른 서브 셋을 만들어 모델을 여러번 훈련시키면 된다. 다음 코드를 보자.

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

def plot_learning_curves(model, X, y):
    X_train, X_val, y_train, y_val = train_test_split(X,y, test_size=0.2)
    train_errors, val_errors = [], []
    for m in range (1, len(X_train)):
        model.fit(X_train[:m], y_train[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_val)
        train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
        val_errors.append(mean_squared_error(y_val, y_val_predict))
    plt.plot(np.sqrt(train_errors), "r-+", linewidth = 2, label = "train set")
    plt.plot(np.sqrt(val_errors), "b-", linewidth = 3, label = "validation set") 
    plt.xlabel("size of train set")
    plt.ylabel("RMSE")
    plt.legend()

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)

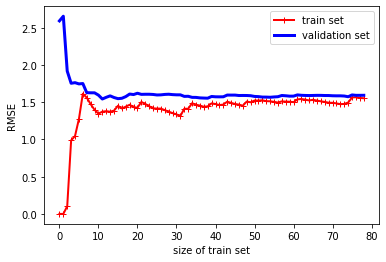
• train set : 훈련 세트가 0개부터 하나씩 증가할때는 모델이 완벽하게 학습해서 rmse가 0부터 시작하고, 샘플이 추가됨에 따라 노이즈와 비선형적 속성때문에 모델이 훈련을 제대로 못하게 된다.
• validation set : 검증 세트(훈련되지않은 데이터)는 모델이 적은수의 훈련데이터로 제대로 일반화를 못했기 때문에, 오차가 초기에 매우 크다가 훈련샘플이 추가됨에따라 학습이 진행되고 오차가 감소한다.

결국 이 학습곡선은 과소적합 모델(비선형 데이터에 선형회귀 직선을 적합했으므로)이고 꽤 높은 오차(RMSE)에서 근접한다.
이 경우 더 나은 변수나 복잡한 모델을 선택해야한다.

이번에는 같은 데이터에 10차 다항회귀모델의 학습곡선을 그려보자.

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

polynomial_regression = Pipeline([
    ("poly_features", PolynomialFeatures(degree=10, include_bias = False)),
    ("lin_reg", LinearRegression())
])

plot_learning_curves(polynomial_regression, X, y)
plt.axis([0,80,0,3])
plt.show()

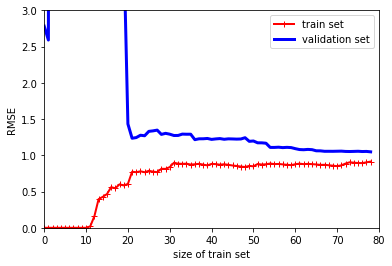
이 학습 곡선은 이전과 비슷해 보이지만 2가지 차이가 있다.

• 훈련 셋(train set)의 오차(RMSE)가 선형회귀보다 낮다.
• 두 곡선 사이에 공간이 있는데, 이는 모델 성능이 검증보다 훈련셋에서 더 낫다는 뜻으로 과대적합 모델의 특징이다. 하지만 더 많은 훈련 샘플을 투입하면 두 곡선이 가까워 질 수 있다.

과대적합 모델을 개선하는 한 방법은, 검증오차가 훈련오차에 가까워 질때 까지 훈련세트를 더 투입하는 것

편향/분산 트레이드 오프

1. 편향
   = 편향은 잘못된 가정으로 인한 것으로, 편향이 큰 모델은 훈련데이터에 과소적합되기 쉽다.(예를들어 비선형에 선형회귀 적합)

2. 분산(variance)
   = 훈련데이터에 있는 작은 변동에 모델이 과도하게 민감하기 때문에 발생, 자유도가 높은 모델(예를들어 고차 다항회귀)이 높은 분산을 가지기 쉬워 훈련데이터에 과대적합 되는 경향이 있다.

3. 줄일 수 없는 오차(irreducible error)
   = 데이터 자체에 있는 노이즈로 인한 오차, 노이즈를 제거하는 방법밖에 없다.

모델의 복잡도가 커지만 분산이 늘어나고, 편향이 줄어든다, 모델이 단순해지면 그 반대이다.
그래서 이를 trade off 라고 부른다.

Reference

도서 [Hands-0n Machine Learning with Scikit-Learn & Tensorflow] 를 공부하며 작성하였습니다.