Yonggeun Shin

Yonggeun Shin

시행착오가 밑거름이 되는 공간

[cs231n] Image classification, kNN 알고리즘과 linear classifier

업데이트:

개요

png

이번 포스팅은 image classification problem의 전반적인 개요를 다룬다. 그리고 이를 해결하기 위한 기존의 접근 방식인 Nearest Neighbor와 Linear classifier에 대한 내용도 포함된다.

Image Classification

jpg

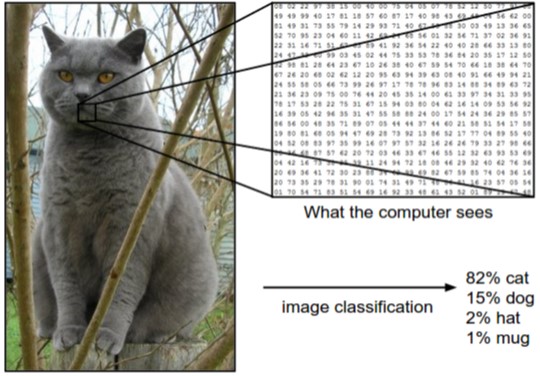
image classification problem은 말그대로 이미지가 주어졌을 때, 어떤 이미지 인지 적절하게 분류하는 문제이다.
위 그림을 보면 사람들은 경험적으로 고양이라는 사실을 알고 대답할 수 있다.
그러나 컴퓨터가 보는 이미지는 우측에 나열된 숫자 형태이다. 정확히는 [0, 255] 사이의 값으로 이루어진 3D(RGB 컬러일 경우) matrix이다.

따라서 우리의 목표는 이러한 숫자들을 기반으로 컴퓨터가 고양이라고 식별하도록 학습시키는 것이다.

Challenges

이러한 이미지를 학습할때 발생하는 여러가지 challenge들이 존재한다.

jpg

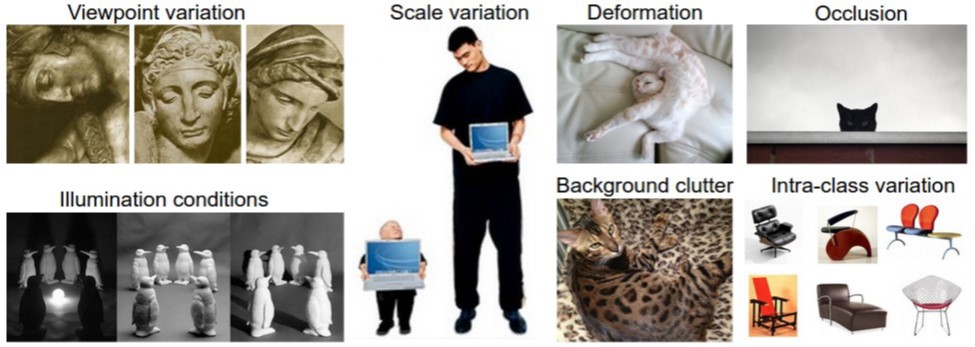
  1. Viewpoint Variation
    • 같은 객체도 찍힌 각도에 따라 다르게 보일 수 있는 문제
    • 사람들은 고양이 옆모습만 봐도 알지만, 컴퓨터는 학습이 잘 안될 수 있다.
  2. Illumination conditions
    • 같은 객체가 조명에 따라 다르게 보일 수 있음
  3. Scale variation
    • 이미지 내에 타겟팅하는 객체의 스케일이 다를 수 있는 문제
    • 작게 찍혔을 수도, 가까이 찍혔을 수도 있다.
  4. Deformation
    • 객체의 모양이 바뀌는 경우 (고양이가 기지개를 켜거나, 사람이 춤을 추거나 등등)
  5. Background clutter
    • 보호색 처럼 객체의 구분이 어려운 경우로, 사람이 봐도 헷갈린다.
  6. Occlusion
    • 객체의 일부가 가려져 있는 경우
  7. Intra-class variation
    • 같은 객체(의자, 자동차 등)도 다른 모양과 색으로 이루어진 사진들이 존재

머신러닝 기반의 이미지 분류기(Image classifier)는 어떻게 만들어야 할까?

대부분의 모델들은 아래와 같은 2단계 프레임워크를 따른다.

  1. 갖고 있는 이미지로 train 하고
  2. 새로운 이미지를 predict 한다.

결국 위와 같은 challenge들(이외에도 여러가지가 있겠지만)을 잘 고려할 수 있도록 train하는 것이 image classification problem의 핵심이 되고, 이에 따라서 여러가지 복잡한 모델들로 발전하게 되는 것이다.


Nearest Neighbor Classifier

초기 접근은 Nearest Neighbor classifer로, 실제로는 거의 사용되지 않지만 접근 방식에 대한 아이디어를 얻을 수 있다.
이는 내가 갖고 있는 이미지들과 가장 가까운(유사한) 이미지라고 판단하면 어떨까? 라는 idea에서 시작되었다.
구체적으로는 2가지 가 있다.

  • 전체 이미지(x값)와 label(y값)을 저장하고,
  • 저장된 샘플들 중 가장 유사한 이미지의 label로 예측한다.

Similarity

그럼 두 이미지 간의 유사도(similarity)는 어떻게 계산해야할까?

2가지 간단한 방법이 있으며, 2장의 이미지 $I_1$와 $I_2$가 있을 때, pixel wise로 $p$에 대하여 연산한다.

  • L1 distance
\[d_1(I_1,I_2) = \sum_{p}|I_1^p-I_2^p|\]

jpg

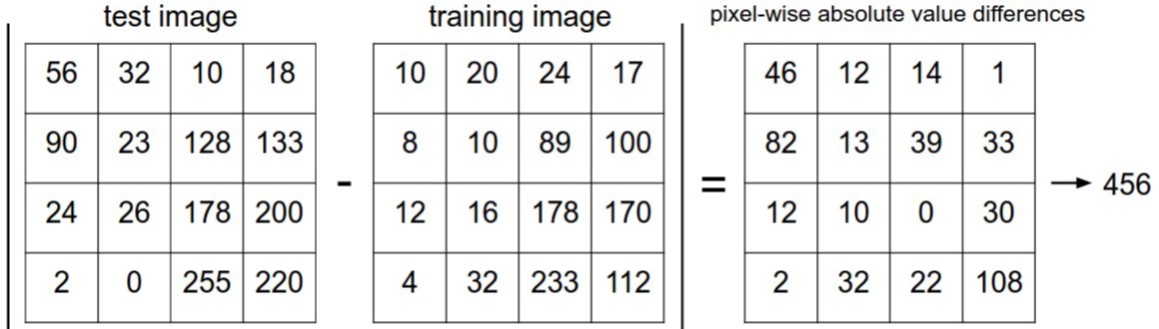
  • L2 distance
\[d_2(I_1,I_2) = \sqrt{\sum_{p}(I_1^p-I_2^p)^2}\]

Python implementation

따라서 Nearest Neighbor를 파이썬으로 구현하면 아래와 같다.

import numpy as np

class NearestNeighbor(object):
    def __init__(self):
        pass
    def train(self, X, y):
        # 모든 training data를 메모리에 저장
        self.Xtr = X
        self.ytr = y
    def predict(self, X):
        # 여러개 이미지를 predict하기 위함
        num_test = X.shape[0]
        Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

        # predict 이미지 1 vs train 이미지 N개 (가장 가까운 train 이미지 추출)
        for i in range(num_test):
            # L1 distance
            distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
            # L2 distance
            # distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))
            
            min_index = np.argmin(distances) # 가장 거리가 가까운 index 추출
            Ypred[i] = self.ytr[min_index]   # Label로 변환
        return Ypred

시간 복잡도는 아래와 같고 predict가 오래걸려 좋지 않다.

  • train : O(1), 메모리에 저장만 하면 됨
  • predict : O(N*M), test이미지 1장당 N개 train 이미지와 비교
    *train(N), test(M)

kNN (k-Nearest Neighbor)

흔히 알고 있는 kNN 알고리즘은 k개의 후보 중에 나은 선택을 하자는 아이디어이다.
즉, 가장 가까운 train 이미지 대신, 가까운 k개의 후보 중에 다수결 투표(majority vote)를 통해 최종적으로 예측하는 방식이다.

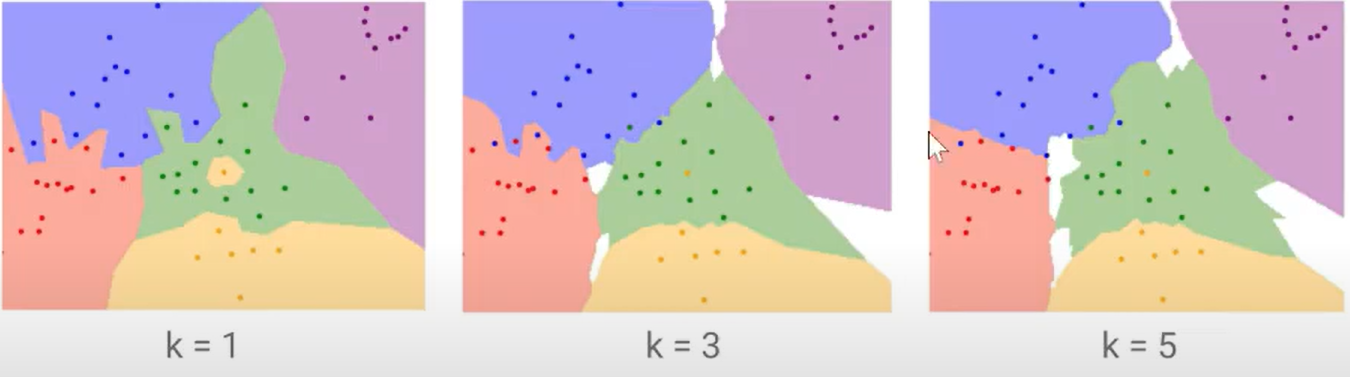
아래 그림은 k 값에 따라 이미지가 분류되는 decision boundary 이다.

PNG

예를 들어 k=1일 때는 가장 가까운 이미지로 예측되기 떄문에, 가운데 섬처럼 노란색 label 주변의 이미지는 노란색으로 예측될 것이다.

그러나 이것은 애초에 잘못 라벨링이 되었을 가능성이 크므로 좀 더 많은 후보(k개)를 참고해서 스무딩을 해주자는 것이다.

따라서 위 파이썬 구현에서, predict할때 2가지만 추가해주면 된다.

  • test image마다 k번째 가까운 train 이미지를 추출
  • k개중 다수에 해당하는 label을 최종 prediction 값으로 선택

Hyperparameters

kNN 알고리즘에서 우리가 선택하야할 사항은 2가지가 있었다.

  1. k 값의 선택
  2. distance 측정 방식

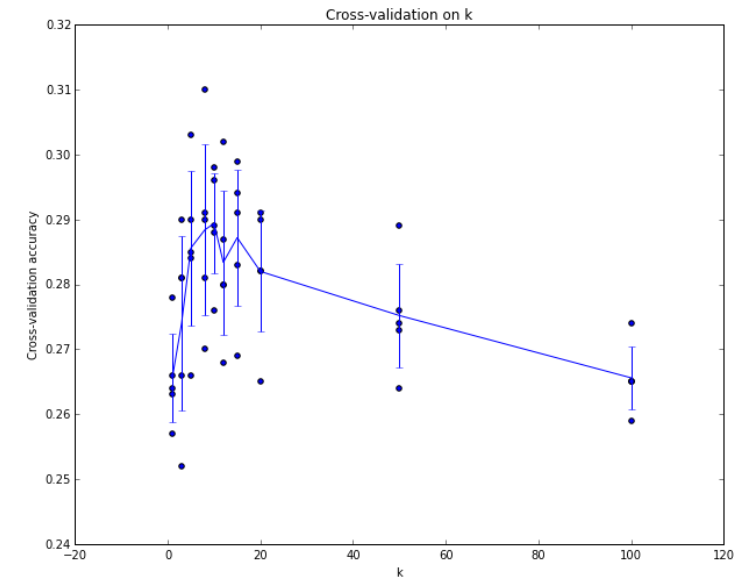
딱히 어떤게 좋다라기 보다는 cross validation과 같은 반복실험을 수행하거나, 어떤 상황에는 어떤게 좋더라라는 경험적인 답변이 많이 존재하는 것 같다.

PNG

위 그림과 같이 반복된 실험을 통해 가장 accuracy가 높게 나타나는 k 또는 distance를 선택할 수도 있을 것이다.

distance 측정의 경우에는 수식의 특성과 데이터의 특성이 잘 부합하는지를 분석해 볼 수 있다.
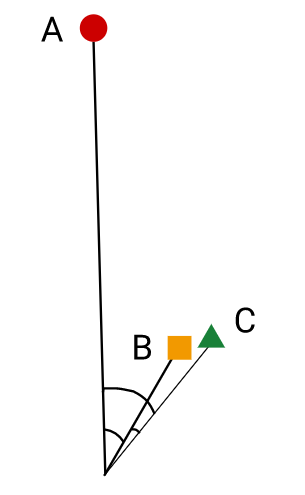
아래 그림과 같이 A,B,C 점이 있고 B가 A와 C중 어디에 분류되는지를 알아보자.

PNG
Source : developers.google.com

  • Cosine similariry : B-C, 벡터 사이의 각도를 봄 (각도가 작을 수록 가깝다)
  • L2 distance : B-C, 직선거리가 작을 수록 가깝다.
  • Dot prodict : B-A, cosine과 벡터 길이 둘다에 비례하여 가까움


Linear classifier

kNN과 같이 단순히 모든 train 데이터와 비교하는 것이 매우 비효율적인 문제가 있었다.
따라서 어떤 이미지를 예측해주는 function을 만들어보자는 의도가 시작된다.

아래 수식은 간단한 linear classifier의 수식이다.

\[f(x_i, W, b)=Wx_i+b\]

이는 $x_i$ 이미지에 어떤 가중치 $W$를 곱하고 편차 $b$를 더한 값으로 새로운 이미지 라벨을 결정하자는 의미다.
즉, 우리는 train 데이터를 통해 parameter인 $W$와 $b$를 결정하면, 새로운 데이터에 대해서는 train 데이터 없이 Paremter를 곱하고 더하여, 예측할 수 있다는 것이다.

따라서 이를 Paremetric approach 라고 한다.

Dimension

PNG

앞의 linear 수식 연산을 위해서는 행렬곱이 필요하다.
위 그림과 같이 image의 dimension이 2x2라면 flatten해서 4x1의 feature($x$)가 있고, 3개의 label이 있다고 할때,

우리가 결정해야할 parameter의 차원은 각각 $W$는 3x4, $b$는 3x1이 된다.
즉, input image의 차원이 D=2x2x1, Label이 K=3이라고 한다면, 아래와 같이 일반화 된다.

  • $W$ : KxD
  • $b$ : Kx1

PNG

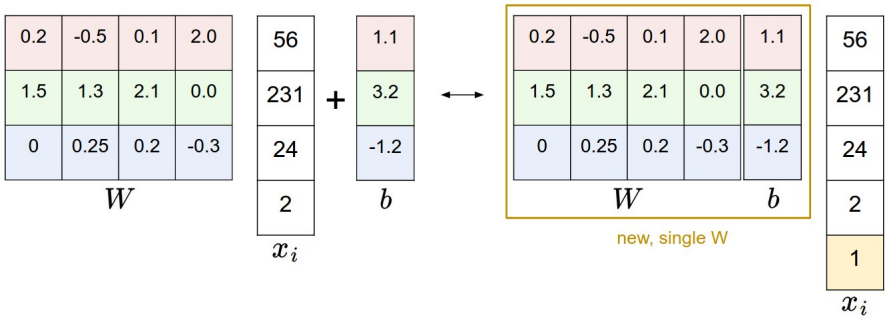
그런데 위 그림과 같이 $b$도 행렬에 포함시켜 한번에 연산할 수 있다.
따라서 notation도 간단해진다.

\[f(x_i, W)=Wx_i\]

이렇게 label마다의 Score들을 산출하고, 이를 기반으로 최종 label로 결정해주는 것이다.


Reference

이 포스팅은 cs231n 수업(by Prof. Li Fei-Fei at Stanford University)과 Machine Learning for Visual Understanding (by 서울대학교 이준석 교수님) 수업을 듣고 공부하며 작성하였습니다.

https://cs231n.github.io/

http://viplab.snu.ac.kr/viplab/courses/mlvu_2021_2/index.html

댓글남기기

참고