[Algorithm] 최단경로 - 다익스트라 (Dijkstra) 알고리즘

업데이트: July 14, 2022

개요

jpg

최단 경로(Shortest path) 알고리즘은 길찾기 문제로, 말 그대로 특정 지점에서 특정 지점까지 가기 위한 최단 경로를 구하기 위한 알고리즘이다.

경로 계산 방식에도 아래와 같은 종류가 있다.

(One-To-One) 한 지점에서 다른 특정 지점까지의 최단경로 구하기
(One-To-All) 한 지점에서 다른 모든 지점까지의 최단경로 구하기
(All-To-All) 모든 지점에서 모든 지점까지의 최단경로 구하기

이번 포스팅은 이 중 2번째 유형(One-To-All)의 대표적인 방법인 다익스트라 (Dijkstra) 알고리즘에 대해 알아보자.

다익스트라 알고리즘

다익스트라 알고리즘은 오래 전에 개발되었지만, 지금까지도 대부분의 경우에 적용되고 있는 파워풀한 알고리즘이다.

앞서 말한것 처럼 그래프에서 특정 노드에서 출발하여 다른 모든 노드로 가는 각각의 최단 경로를 구해주는 알고리즘이다.
단, 모든 링크의 가중치(길이)는 양의 정수 값이어야 한다.

동작 방식

구체적인 동작 방식은 아래와 같다.

출발 노드를 설정하고, 최단 거리 테이블을 초기화한다.
방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택한다.
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 갱신 : 현재 테이블의 최단거리보다, 해당 노드를 거쳐가는 비용이 작으면 작은 경로로 교체
3~4의 과정을 반복한다.

글만 봤을때는 직관적으로 이해가 잘 안된다. 아래와 같이 8개의 노드가 있는 그래프가 있을 때 1번 노드로 출발하는 경우를 알아보자.

최단거리 테이블은 각 노드에 대해 주어지며, 각 값들은 1번 노드에서 x번 노드로 가는 최단 경로를 의미한다.
처음에는 1번노드에서 자기 자신의 거리는 0이고, 나머지는 무한(INF)값으로 초기화한다.

png

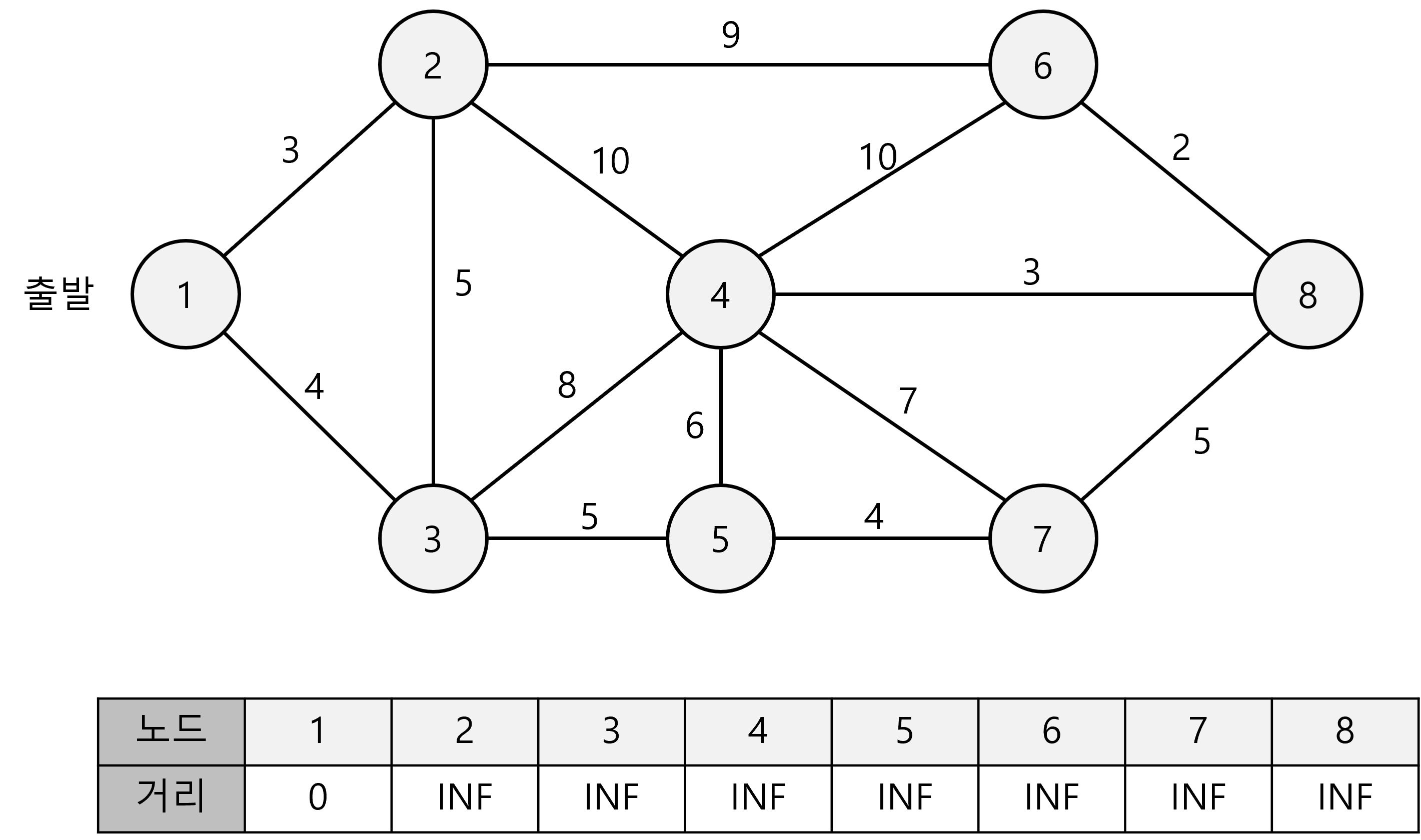
Step 1: 출발인 1번 노드를 선택하고, 해당 노드를 거쳐 갈 수 있는 다른 노드들(2번과 3번)의 거리를 계산하여 갱신한다. 무한값 보다 작으므로 갱신된다.

png

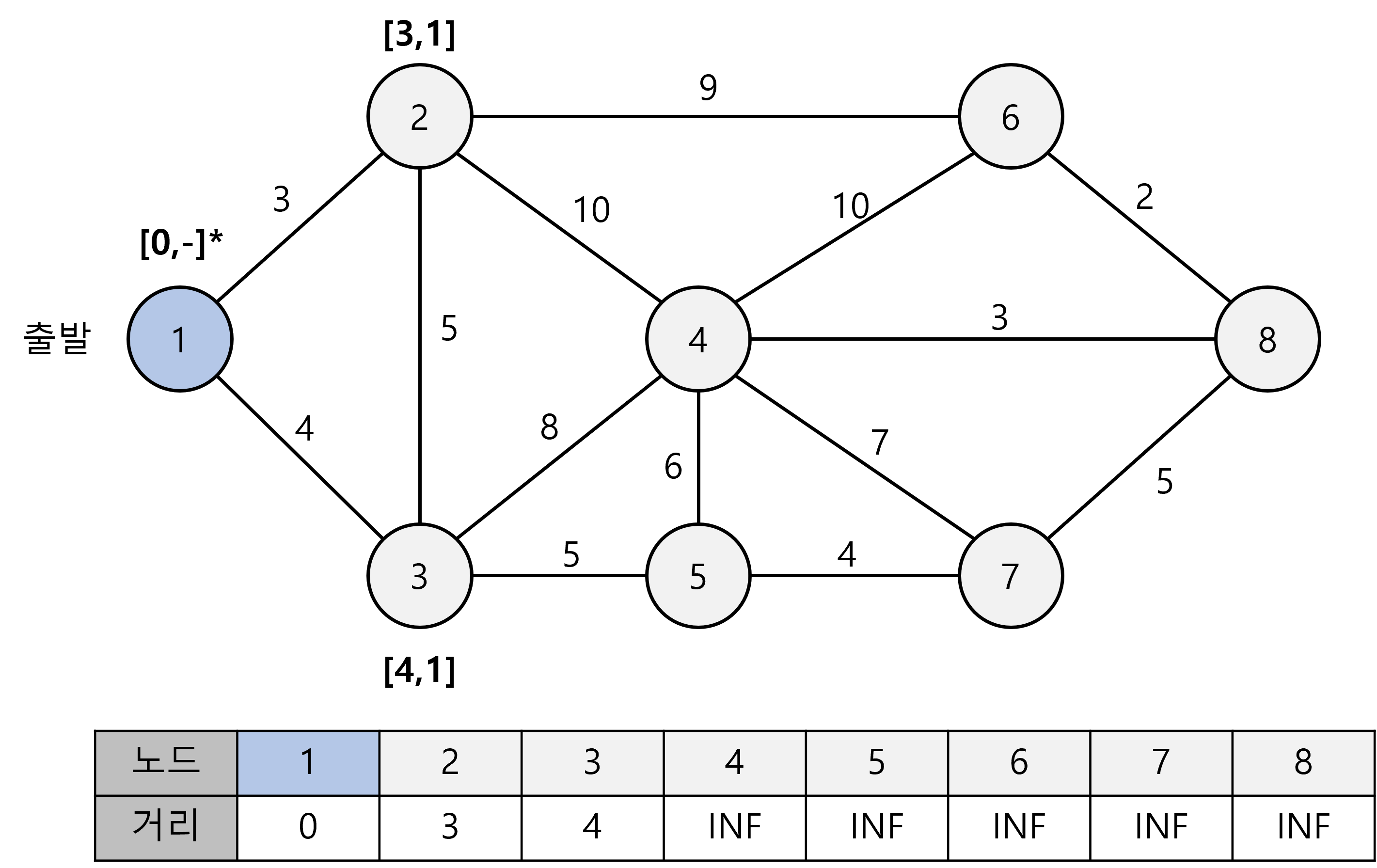
노드 위의 식별값은 [최단거리, 이전 노드](*)로 표현되며, 방문한 적이 있는 노드는 더이상 갱신할 필요가 없어 * 표시를 한다.

Step 2: : 방문하지 않은 노드 중 가장 짧은 최단거리 노드(2번)를 선택하고 해당 노드를 거쳐갈 수 있는 다른 노드의 최단 거리 값을 갱신한다.

png

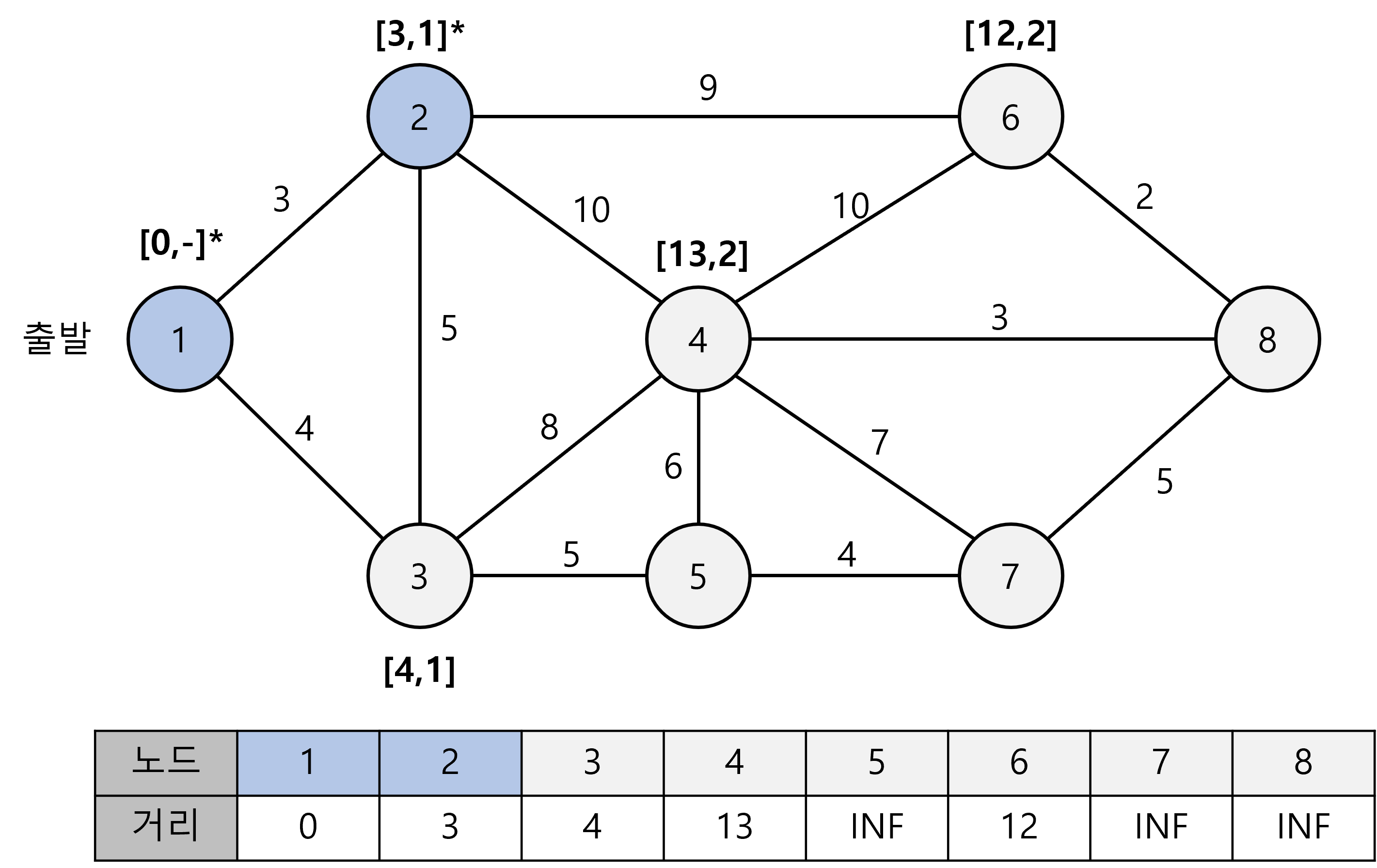
Step 3: 마찬가지로 3번 노드를 선택하여 반복

png

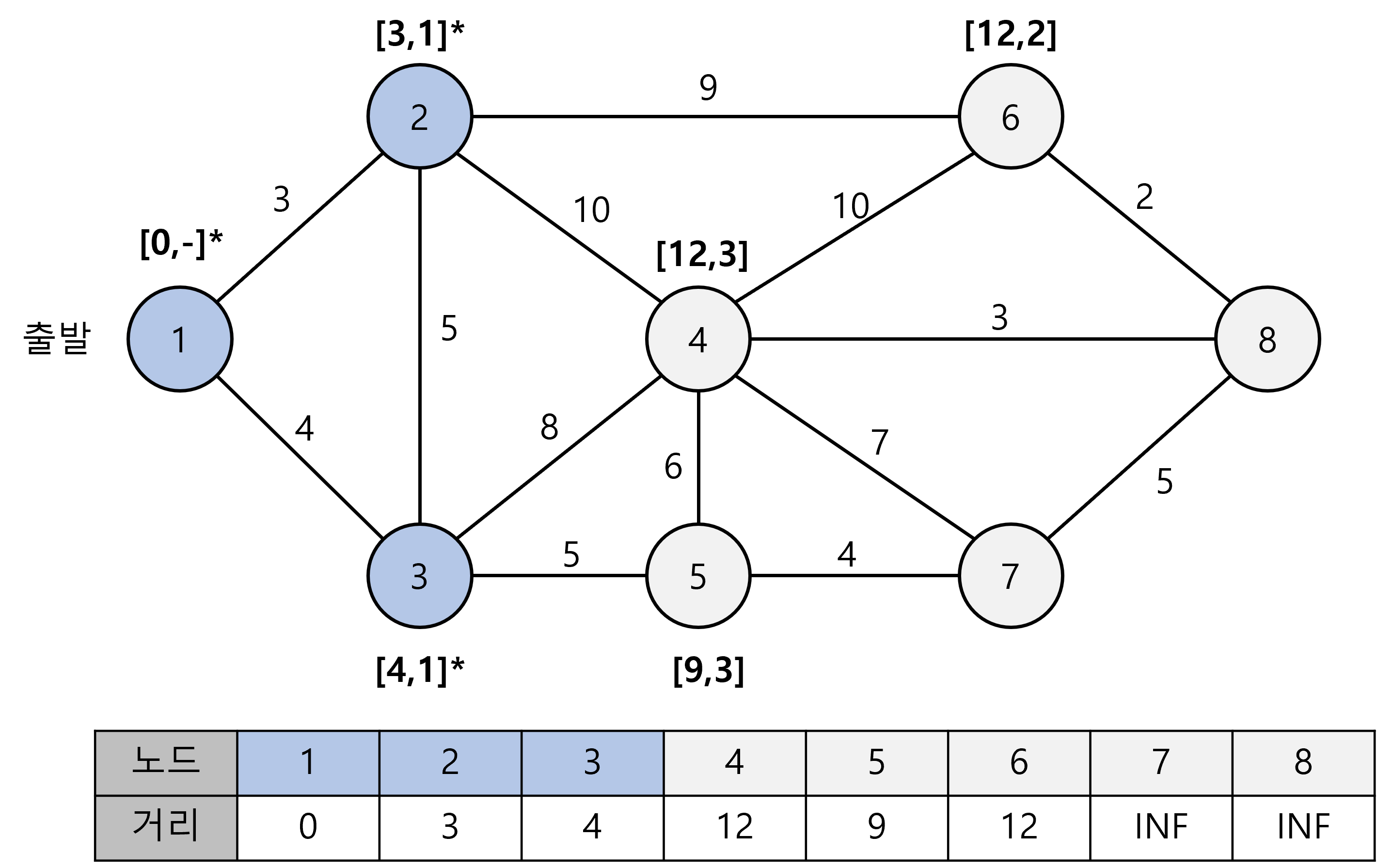
여기서 중요한점은 4번 노드의 최단거리는 2번 노드에 의해 13이었는데 이번 단계에서 3번 노드에 의해 12로 갱신된다는 것이다.
즉, 다익스트라가 One-To-All 방식이므로 모든 Scan이 끝날떄까지 목적지 최단거리를 알기 어렵다.

이 과정을 계속 반복하면 결국 아래와 같은 결과와 최단거리 테이블을 얻을 수 있다.

png

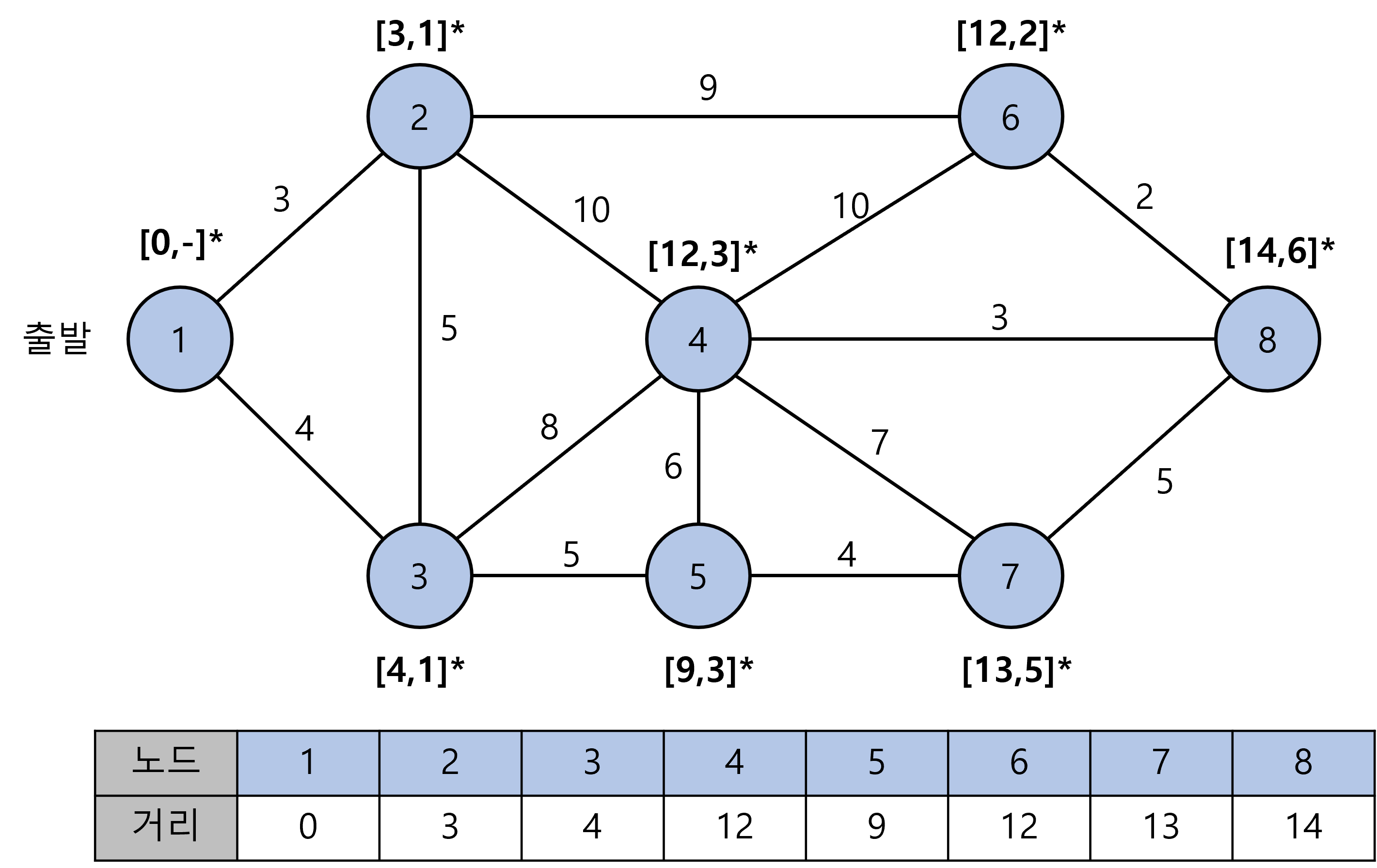
결국 1번 노드에서 다른 모든 노드로 가는 경로와 최단거리를 알 수 있고, 목적지 8번 노드까지의 거리는 14임을 알 수 있다.
최단경로의 경우 각 노드의 부모노드를 쭉 트랙킹하면 8<-6<-2<-1를 얻을 수 있다.
(8번 노드의 부모노드는 6번 노드)

구현 코드 1 - 기본

경로까지 저장하지는 않고, 특정 노드에서 모든 노드까지의 최단경로길이만을 출력하는 코드이다. 위 동작방식을 그대로 코드로 옮긴 것이다. 위 예제는 양방향으로 구성된 그래프 인데, 만약 하나의 링크 정보만 주어지고 양방향이라고 한다면, graph를 저장할때 반대방향도 저장해야함을 유의하자.

n,m=map(int,input().split())
start = int(input())
graph = [[] for _ in range(n+1)]

visited=[False]*(n+1)
distance=[int(1e9)]*(n+1)

for _ in range(m):
    a,b,c = map(int, input().split())
    # a번 노드에서 b번 노드로가는 비용이 c인 입력
    graph[a].append((b,c))
    graph[b].append((a,c))  # 양방향일경우 반대방향도 저장 주의


def get_smallest_node():
    min_value=int(1e9)
    index=0
    for i in range(1,n+1):
        if distance[i]<min_value and not visited[i]:
            min_value = distance[i]
            index=i
    return index

def dijkstra(start):
    # 출발 기록
    distance[start]=0
    visited[start]=True
    for j in graph[start]:
        distance[j[0]]=j[1]
        
    # start 제외한 노드 수 만큼 반복
    for i in range(n-1):
        # 최단 거리 노드 추출
        now=get_smallest_node()
        # 방문처리
        visited[now]=True
        
        for j in graph[now]:
            # 현재 노드에서 갈 수 있는 다른 노드 cost 계산
            cost = distance[now]+j[1]
            # 기존 것 보다 더 짧은 경우 갱신
            if cost < distance[j[0]]:
                distance[j[0]]=cost
    
dijkstra(start)
                
for i in range(1,n+1):
    if distance[i]==int(1e9):
        print("INFINITY")
    else:
        print(distance[i])

구현 코드 2 - heapq 방식

위 기본 구현코드에서는 다음 방문노드를 선택하기 위해 get_smallest_node()함수에서 매번 모든 노드를 확인하여 방문하지 않은 노드 중 가장 짧은 최단거리를 갖는 노드를 선택한다.

이로 인해 계산 복잡도가 올라가는데, 힙(heap) 자료구조를 이용하면 이 부분을 개선시킬 수 있다.

힙은 전에 포스팅했던 스택과 큐에서 우선순위를 가진 큐 자료구조로, 우선순위 큐를 위한 자료구조이다.

스택(Stack) : 선입후출
큐(Queue) : 선입선출
힙(Heap) : 우선순위가 높은 데이터를 먼저 추출 (우선순위 큐)

파이썬에서는 heapq라이브러리를 이용할 수 있고, 최소 힙 구조를 이용한다.

구체적으로는 큐 내부에 [(거리,노드),(거리,노드),..]와 같은 식으로 저장되며, 거리가 가장 작은(최소 힙) 튜플이 추출된다. 삽입은 heapq.heappush(리스트, (거리,노드)), 추출은 heapq.heappop(리스트)로 이루어진다.

정리하면, 다익스트라 동작 방식에서 매번 모든 노드를 확인하여 최단거리 노드를 선택하는 것을 힙 자료구조를 이용한 우선순위 큐로 대신하여 연산의 효율성을 개선한다.

INF = int(1e9)

n,m=map(int,input().split())
start = int(input())
graph=[[] for i in range(n+1)]
distance=[INF]*(n+1)

for _ in range(m):
    a,b,c = map(int, input().split())
    graph[a].append((b,c))

def dijkstra(start):
    q=[]
    heapq.heappush(q,(0,start))
    distance[start]=0

    while q:
        # 가장 최단거리가 짧은 노드에 대한 정보 꺼내기
        dist, now = heapq.heappop(q)
        # 현재 처리된적이 있는 노드라면 pass
        if distance[now]<dist:
            continue
        # 현재 노드와 연결된 다른 인접한 노드들을 확인
        for i in graph[now]:
            cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[i[0]]:
                distance[i[0]]=cost
                heapq.heappush(q,(cost,i[0]))
                
dijkstra(start)

for i in range(1,n+1):
    if distance[i]==INF:
        print("INFINITY")
    else:
        print(distance[i])

동작 방식은 동일하다. 별도의 방문처리 리스트visited가 필요하지 않다.

출발노드를 우선순위 큐에 넣는다.
우선순위 큐에서 데이터를 추출한다.
이미 갱신된 노드라면 Pass한다.
우선순위 큐에서 꺼낸 노드를 기준으로 방문할 수 있는 다른 노드들의 최단 거리 테이블을 갱신하고 큐에 담는다.
1~4를 반복한다.

2번에서 이미 갱신된 노드를 판별하는 것이 조금 다르고 헷갈릴 수 있는데 다음과 같이 정리해본다.

기본 : 방문하지 않은 노드 중 -> 최단 거리 노드 추출
힙 : 큐에서 나온 노드의 거리가 최단거리 테이블보다 크다면 갱신된 것이라고 보고 패스함

최단경로 추적하기

앞의 구현방식은 단순히 출발 노드로 부터 각 노드까지의 최단경로 길이만을 출력하는 방식이였다.

그러나 앞서 설명한 것처럼 갱신할때 최단 거리와 이전의 부모 노드를 같이 기록해주기만 하면 된다.
즉, 현재 노드를 거쳐 다른 노드로 갈 최단거리에 대해 그 현재노드가 무엇인지도 같이 기록해주자.

import heapq
INF = int(1e9)

n,m = 8,14 # 노드 수
start = 1 # 출발 노드
graph=[[] for i in range(n+1)]
# 최단거리 + 부모노드 저장 테이블 생성
distance=[[INF,i] for i in range(n+1)]

# 양방향 입력
# 노드 a와 노드 b의 비용 c
for _ in range(m):
    a,b,c = map(int, input().split())
    graph[a].append((b,c))
    graph[b].append((a,c))

def dijkstra(start):
    q=[]
    heapq.heappush(q,(0,start))
    distance[start][0]=0

    while q:
        # 가장 최단거리가 짧은 노드에 대한 정보 꺼내기
        dist, now = heapq.heappop(q)
        # 현재 처리된적이 있는 노드라면 pass
        if distance[now][0]<dist:
            continue
        # 현재 노드와 연결된 다른 인접한 노드들을 확인
        for i in graph[now]:
            cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[i[0]][0]:
                distance[i[0]][0]=cost # 최단거리 갱신
                distance[i[0]][1]=now  # 부모노드 저장
                heapq.heappush(q,(cost,i[0]))
                
dijkstra(start)

# 결과 출력
for i in range(1,n+1):
    length,_= distance[i] # 최단 길이
    parent_node=i
    path=[]
    while parent_node!=1:        
        path.append(parent_node)    
        _,parent_node = distance[parent_node]
        distance[parent_node]
    path.append(1)
    print("%s번 노드 : %s (%s)" % (i,">".join(map(str,path[::-1])),length))

1번 노드 : 1 (0)
2번 노드 : 1>2 (3)
3번 노드 : 1>3 (4)
4번 노드 : 1>3>4 (12)
5번 노드 : 1>3>5 (9)
6번 노드 : 1>2>6 (12)
7번 노드 : 1>3>5>7 (13)
8번 노드 : 1>2>6>8 (14)

결과 출력 시, 현재 노드로 부터 부모 노드를 계속 타고가다가 루트 노드(1번)을 만나면 종료하는 방식으로 추적한다.

Reference

이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈

https://hongjw1938.tistory.com/47

Twitter Facebook LinkedIn

Yonggeun Shin

[Algorithm] 최단경로 - 다익스트라 (Dijkstra) 알고리즘

개요

다익스트라 알고리즘

동작 방식

구현 코드 1 - 기본

구현 코드 2 - heapq 방식

최단경로 추적하기

Reference

공유하기

댓글남기기

참고

[Git] Git & Github의 동작원리 이해하기 및 주요 명령어 정리

[GIS] Uber h3와 kepler.gl을 활용한 공간분석

[GIS] 도로 네트워크 데이터를 활용한 도시의 공간단위 분할

[pytorch] pretrained model의 활용과 fine tuning 하기