[논문리뷰] NCF: Neural Collaborative Filtering
업데이트:
Abstract
Neural Collaborative Filtering 논문 링크
- Neural Network가 성공적으로 적용되고 있던 시기, 추천시스템에 적용한 경우는 적었음
- Implicit Feedback 문제에서 Collaborative Filtering (CF)에 Neural Network를 적용
- CF는 Matrix Factorization을 사용 → linear
- NCF(Neural Collaborative Filtering): inner product를 신경망으로 대체
- user-item interaction을 학습하기 위해 MLP 사용
- 실험 결과
- 2개 실제 데이터 셋 이용
- layer를 깊게 쌓을 수록 → 성능이 좋아지는 경향
1. Introduction
- 다양한 Collaborative Filtering 방법론 중, Matrix Factorization (MF) 기법이 가장 인기있음
- MF 계열의 다양한 고도화 연구가 시도되었음
- 그러나, 단순히 inner product를 사용하기 때문에 성능이 개선되지 못하는 한계가 있음
- linear하게 곱하는 방법이기 때문에, user interaction 데이터의 풍부한 정보를 담지 못함
- Contribution
- Neural Network를 기반으로 user-item latent feature를 모델링
- 기존 MF는 NCF의 Special case가 됨을 증명
- 두개의 실제 데이터셋으로 실험 및 검증
2. Preliminaries
2.1 Learning From Implicit Data
- M: User의 수
- N: Item의 수
-
$Y\in R^{M \times N}$: User-Item interaction matrix

- interaction(=1)이 선호도를 나타내지는 않음 (implicit feedback)
- 반대로 0이라도 비선호를 나타내는 것은 아님
- 따라서 Implicit feedback에서 이러한 noise가 있을 수 있어서 학습이 어려움
- 관심으로는 생각할 수 있지만, 부정적인 피드백 데이터가 없음
- Imlicit feedback problem
- Y(matrix)에서 관찰되지 않은 score를 예측하는 것
- 목적함수를 최적화하기 위해 2개의 목적함수를 주로 사용함
- Pointwise Loss: regression 문제 → target y와 y_hat의 차이를 최소화
- Pairwise Loss: observed 값들이 unobserved보다 더 높은 순위를 매겨야한다는 아이디어 → target y와 y_hat의 marging을 최대화
- NCF는 y_hat을 위한 parmeter를 추정하기위해 neural network를 사용하므로, 두 방법의 아이디어를 모두 반영하는 셈임
2.2 Matrix Factorization
- Latent vector notation
- $p_u$: user
- $q_i$: item
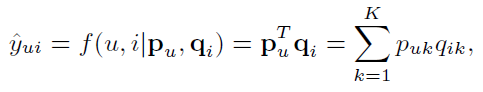
-
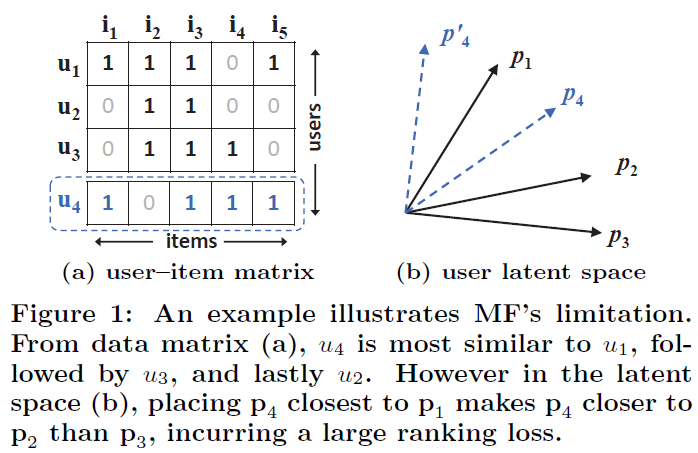
Inner product와 같은 linear한 방식에서 복잡한 관계를 표현하는데 어려움을 지적
-
user 1, 2,3 만 존재 시 → 검은 선으로 표현된 유사도
$s_{23}(0.66)>s_{12}(0.5)>s_{13}(0.4)$
-
New user 4 추가 → 파란 점선
$s_{41}(0.6)>s_{43}(0.4)>s_{42}(0.2)$
→ 표현할 수 없음
-
- 위 예시에서 MF의 한계를 지적
- 저차원 공간에서 linear하게 mapping하는데서 발생하는 한계
- 차원(K)을 증가시켜볼 수 있으나, model이 복잡해지고 generalization이 어려워짐
⇒ DNN으로 해결해보자!
3. Neural Collaborative Filtering
- 진행 순서
- NCF의 Framework
- MF가 NCF로 일반회될 수 있음을 증명
- MLP에 대한 설명
- MF와 MLP를 결합하기 위한 모델 제시
3.1 General Framework
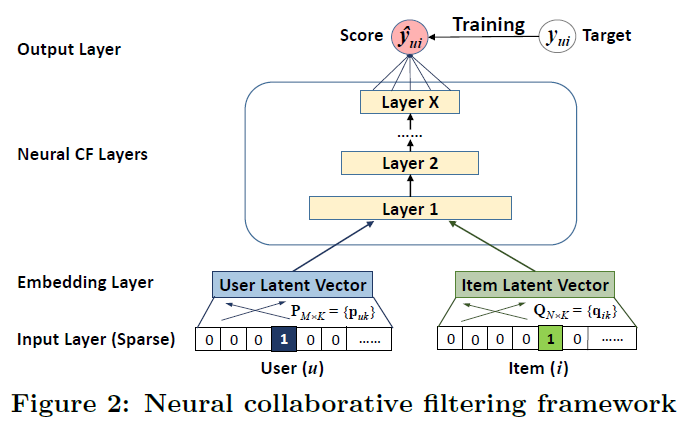
- Input Layer: user-item의 one-hot encoding한 sparse vector를 사용
- $v_u^U$: User vector
- $v_i^I$: Item vector
- Embedding Layer: FC Layer를 기반으로 Sparse vector를 dense vector로 맵핑
-
이 dense vector를 흔히 얘기하는 latent vector라고 생각할 수 있음
$P^Tv_u^U$: User latent vector
$Q^Tv_i^I$: Item latent vector
-
- Neural CF Layers: User와 Item vector 를 Input으로 MLP를 통과하는 과정
- Output Layer: 최종 prediction 출력 및 loss 계산하는 과정
- Pointwise loss를 기반으로 $\hat{y}{u,i}$(prediction)과 $y{u,i}$(target)의 loss 계산
-
model formulation
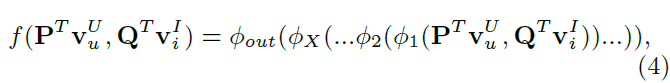
- mapping function들을 거쳐서 output을 도출
3.1.1 Learning NCF → Loss function
- notation
- $\mathcal{Y}$: $\hat{y}_{u,i}=1$인 관측치들
- $\mathcal{Y}^-$: $\hat{y}_{u,i}=0$인 관측치들
- target y가 Binary 값이기 때문에, 일반적인 Squared Error가 적합하지 않음
- 확률값으로 설명하기 위해 $\hat{y}_{ui}$의 범위를 [0,1]로 제한
- output layer에서 sigmoid 같은 것을 쓰면 됨
-
따라서 Binary cross Entropy loss를 적용
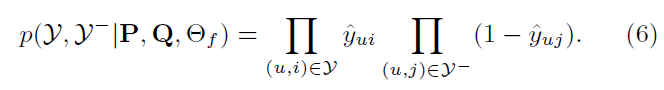
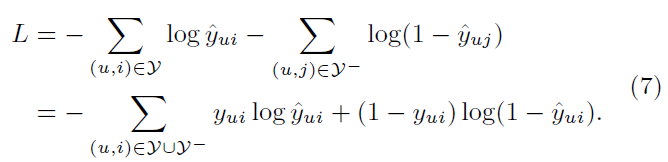
-
$L$(loss)는 -log를 씌운 값
-
3.2 General Matrix Factorization (GMF)
- MF가 NCF의 special case인 이유를 설명 → Embedding Layer
-
Embedding Layer에서 Neural CF로 들어가는 부분을 다음과 같이 표현
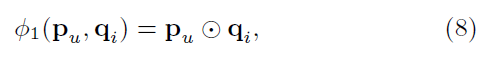
- $p_u$: $P^Tv_u^U$ → user latent vector
- $q_i$: $Q^Tv_i^I$ → item latent vector
- $\odot$: element-wise(inner) product
-
풀어 쓰면 다음과 같음
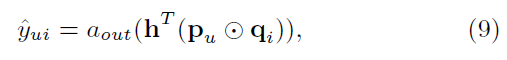
- $a_{out}$와 $h$는 activation function
- 여기서 $a_{out}$를 identity function(항등함수), h를 vector of 1로 치환하면 결국 MF
- 이와 같이 다양한 변형을 만들 수 있다는 점에서, 위 표현이 general form임
- 본 연구에서는 General NCF(GMF)를 다음과 같이 정의
- $h$: learnable parameter
- $a_{out}$: sigmoid function
- Loss func : log loss (BCE loss)
3.3 Multi-Layer Perceptron (MLP)
- Embedding Layer (User, Item)를 받을때, concatenate하는 방법은 user-item latent features간의 interaction 고려하지 않음
- GMF는 fixed element-wise product($\odot$)로 수행되고 linear하게 구성되어 있음
-
MLP를 기반으로 non-linearity를 반영할 수 있도록 하였음
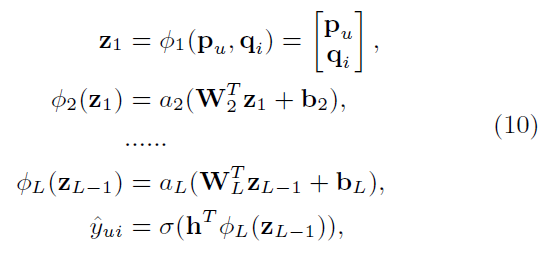
- $\phi$: mapping function
- $W_x$: x-th layer의 weight matrix
- $b_x$: x-th layer의 bias vector
- $a_x$: x-th layer의 activation function
- Activation Function (특징 복습)
- sigmoid → Saturation, zero centered 문제
- Tanh → zero centered 문제만 해결
- ReLU (적용) → Dead ReLU Problem 존재
3.4 Fusion of GMF and MLP
- GMF와 MLP를 결합하는 모델을 제시
-
심플한 방법: GMF와 MLP가 동일한 embedding layer를 share하고, 결과값을 결합
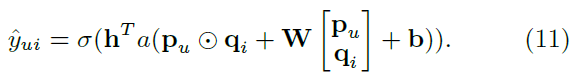
- 이렇게 구성할 경우 GMF와 MLP의 dimension이 같아야 하는 제약이 생김
- 두 모델의 최적의 Embedding size는 다를 수 있음
-
더 flexible하게 두 모델을 결합하기 위한 방법은?
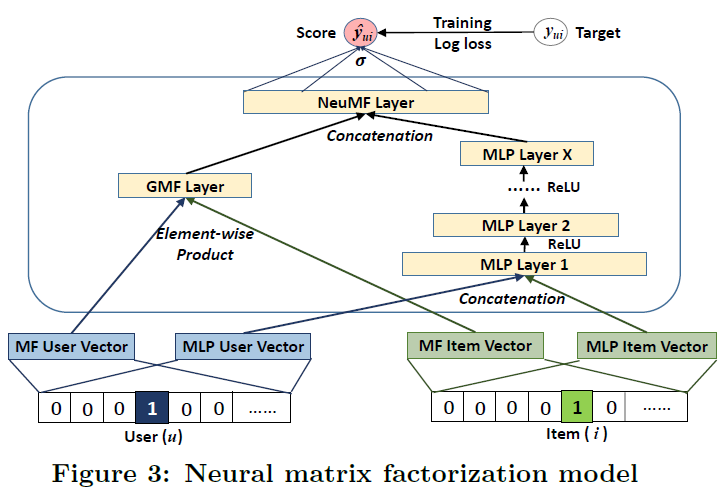
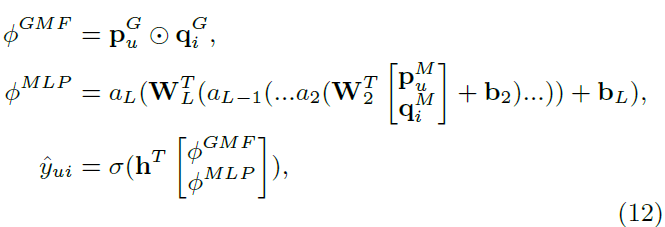
- GMF와 MLP를 별도의 embedding으로 학습하고,
- 마지막 hidden layer에서 concatenate해서, prediction하는 방법을 채택
*embedding layer단에서 왜 line이 교차되어 있지?
Pytorch Implementation
class NCF(nn.Module):
def __init__(self, user_num, item_num, factor_num, num_layers, dropout, model):
super(NCF, self).__init__()
self.dropout = dropout
self.embed_user_GMF = nn.Embedding(user_num, factor_num)
self.embed_item_GMF = nn.Embedding(item_num, factor_num)
self.embed_user_MLP = nn.Embedding(
user_num, factor_num * (2 ** (num_layers - 1)))
self.embed_item_MLP = nn.Embedding(
item_num, factor_num * (2 ** (num_layers - 1)))
MLP_modules = []
for i in range(num_layers):
input_size = factor_num * (2 ** (num_layers - i))
MLP_modules.append(nn.Dropout(p=self.dropout))
MLP_modules.append(nn.Linear(input_size, input_size//2))
MLP_modules.append(nn.ReLU())
self.MLP_layers = nn.Sequential(*MLP_modules)
predict_size = factor_num * 2
self.predict_layer = nn.Linear(predict_size, 1)
def forward(self, user, item):
embed_user_GMF = self.embed_user_GMF(user)
embed_item_GMF = self.embed_item_GMF(item)
output_GMF = embed_user_GMF * embed_item_GMF
embed_user_MLP = self.embed_user_MLP(user)
embed_item_MLP = self.embed_item_MLP(item)
interaction = torch.cat((embed_user_MLP, embed_item_MLP), -1)
output_MLP = self.MLP_layers(interaction)
concat = torch.cat((output_GMF, output_MLP), -1)
prediction = self.predict_layer(concat)
return prediction.view(-1)
Pre-training
-
모델의 수렴과 성능을 위해, GMF와 MLP의 pre-trained 모델로 initialize하는 방법을 제시
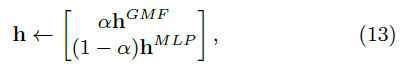
- Random initialization으로 convergence 할 때까지 학습
- 학습된 parameter를 초기값으로 사용
- $\alpha$값을 설정해서, 두 모델을 가중합
-pre-training에는 Adam 사용
to initialize NeuMF using the pre-trained models of GMF and MLP.
4. Experiments
- RQ1: NCF모델이 implicit CF에서의 SOTA 성능을 능가할 수 있는가?
- RQ2: Log loss와 Negative sampling의 효과
- RQ3: layer가 deep해질수록 도움이 되는지?
4.1 Experimental Settings
-
Datasets

- Evaluation Metric
-
Leave-one-out
→ 교차검증시 test set을 data point 1개씩 돌아가며 검증
→ 모든 data로 각각 test를 하므로, randomness를 없앨 수 있으나, 너무 오래걸림
-
Hit Ratio@K
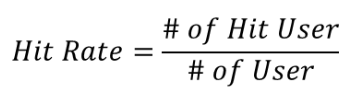
- 사용자가 선호한 아이템 중 1개를 제외
- 나머지 아이템들로 추천 시스템을 학습
- 사용자별로 K개의 아이템을 추천, 앞서 제외한 아이템이 포함되면 Hit
- 전체 사용자 수 대비 Hit한 사용자 수 비율 계산
-
NDCG@K
- Relevance → user-item의 관련도
-
Cumulative Gain (CG) → relevance의 합
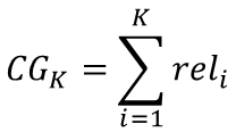
-
Discounted Cumulative Gain (DCG) → 순서에 따라 discount 적용
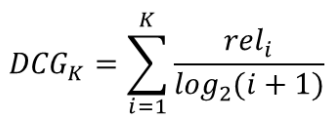
-
Ideal Discounted Cumulative Gain (IDCG) → 최대 DCG 값 (최적으로 추천했을 떄)
(DCG에서 user별 추천 아이템 수가 다른 문제를 위한 scaling)
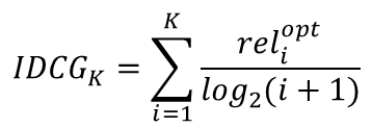
-
Normalized DCG (NDCG) → DCG를 IDCG로 scaling 한 것 (1에 가까울 수록 좋음)
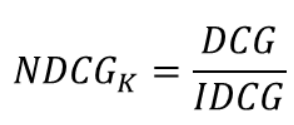
-
- Baseline ⇒ user-item의 관계를 모델링하는 방법론들을 위주로 비교
- ItemPop.
- ItemKNN
- BPR
- eALS → MF계열 SOTA
- Parameter Settings
- four negative instances per positive instance.
- Param initialize: Radom (with Gaussian Distribution)
- Optimization: mini-batch Adam
-
predictive facotrs(마지막 은닉층의 output dim): [8,16,32,64]
→ baseline과 용어를 통일하기 위함
- Batch size: [128; 256; 512; 1024]
- Learning rate: [0.0001 ,0.0005, 0.001, 0.005]
- NeuCF layer(3개)
- embedding size: 16
- $\alpha$=0.5 (pre-trained)
4.2 Performance Comparison (RQ1)
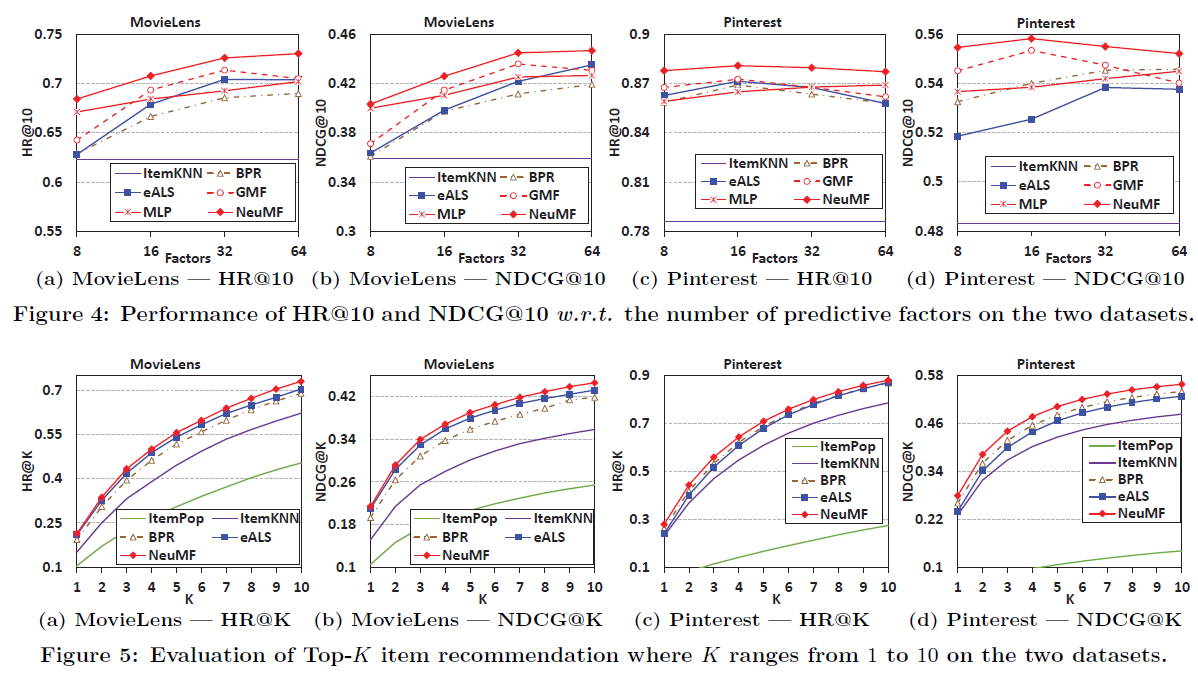
- Figure 4
- 기본적으로 eALS와 BPR을 능가하며 SOTA를 달성
- 개별 모델인 GMF와 MLP 자체도 성능이 높게나옴 → eLAS보다 높을때도 존재
- Figure 5
- 상위 K개에 대한 추천 성능 → NeuMF의 일관된 우수성을 보여줌
4.3 Log Loss with Negative Sampling (RQ2)
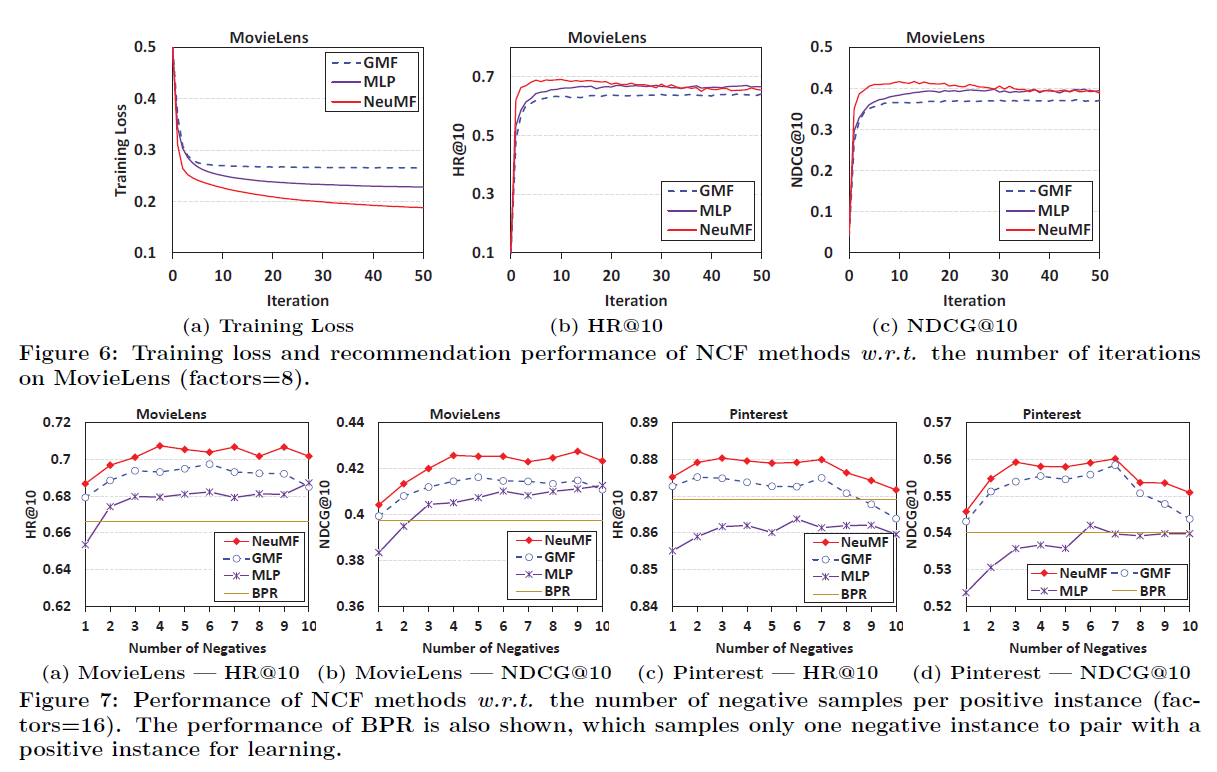
- Figure 6. (MovieLens에서 iteration에 따른 성능)
- Iteration이 증가함에 따라 성능(Training Loss)도 증가하며, NeuMF가 제일 좋음 → Log Loss를 최적화하는게 합리적이라는 얘기
- Figure 7.
- Pointwise loss는 Pairwise objective function와 달리, negative과 positive intance를 유연하게 샘플링할 수 있는 장점이 있음
- Negative sampling ratio를 증가시킬 수록 성능 또한 증가 → 3 ~ 6 정도가 좋음
4.4 Is Deep Learning Helpful? (RQ3)
-
Deep learning의 효과를 보기 위해, hidden layer 수에 따른 성능 비교
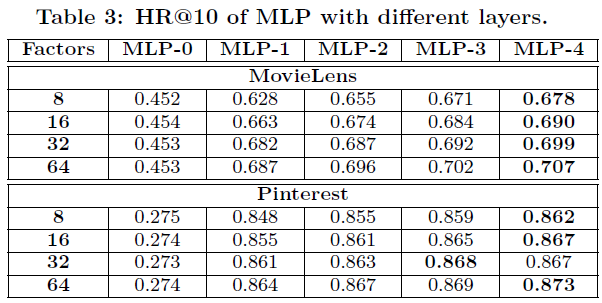
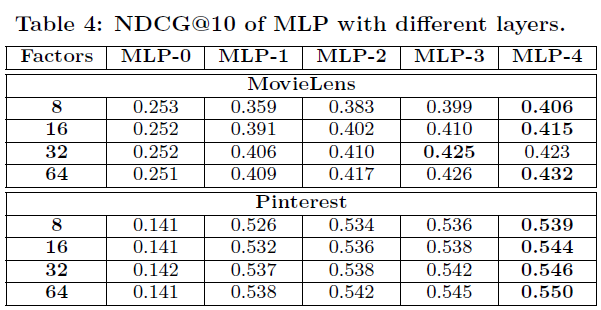
- Layer를 쌓을수록 성능이 올라감(MLP-4)
- hidden layer가 없는 경우(MLP-0)는 확실히 성능이 저하되는 것을 볼 수 있음
Reference
- https://hardenkim.tistory.com/171
- https://leehyejin91.github.io/post-ncf/
- https://github.com/supkoon/neuralCF_tf2/blob/main/NeuralMF.py
- 구현





댓글남기기