[클러스터링] 비계층적(K-means, DBSCAN) 군집분석

개요

군집분석(clustering)이란 개체들을 분류(classification)하기 위한 기준이 없는 상태에서 주어진 데이터의 속성값들을 고려해 유사한 개체끼리 그룹(클러스터)화하는 방법이다. 그룹내 차이를 줄이고 그룹간 차이는 최대화 하도록 하여 대표성을 찾는 원리로 구현되는 것이 일반적이다.
즉, 비지도 학습(Unsupervised Learning)에 해당된다.

군집분석의 유형

다양한 군집분석(Clustering) 방법들이 생겨나고 있지만 큰 유형은 다음과 같다.

• 비계층적 군집분석(Non-Hierarchical Clustering)
  • 중심 기반(Center-based) : K-means
  • 밀도 기반(Density-based) : DBSCAN
• 계층적 군집분석(Hierarchical Clustering)

이번 포스팅에서는 먼저 비계층적 군집분석 방법인 K-means와 DBSCAN에 대해 세부적으로 알아보고 Python으로 구현해보자.

비계층적 군집분석

비계층적 군집분석(Non-Hierarchical Clustering)이란, 말그대로 계층을 두지않고 그룹화를 할 유사도 측정 방식에 따라 최적의 그룹(cluster)을 계속적으로 찾아나가는 방법이다.

K-means

K-means는 중심기반(Center-based) 클러스터링 방법으로 “유사한 데이터는 중심점(centroid)을 기반으로 분포할 것이다”는 가정을 기반으로 한다.

n개의 데이터와 k(<=n)개의 중심점(centroid)이 주어졌을때 각 그룹 내의 데이터와 중심점 간의 비용(거리)을 최소화하는 방향으로 계속 업데이트를 해줌으로써 그룹화를 수행하는 기법이다.

말이 어려우니 아래 그림과 함께 보자

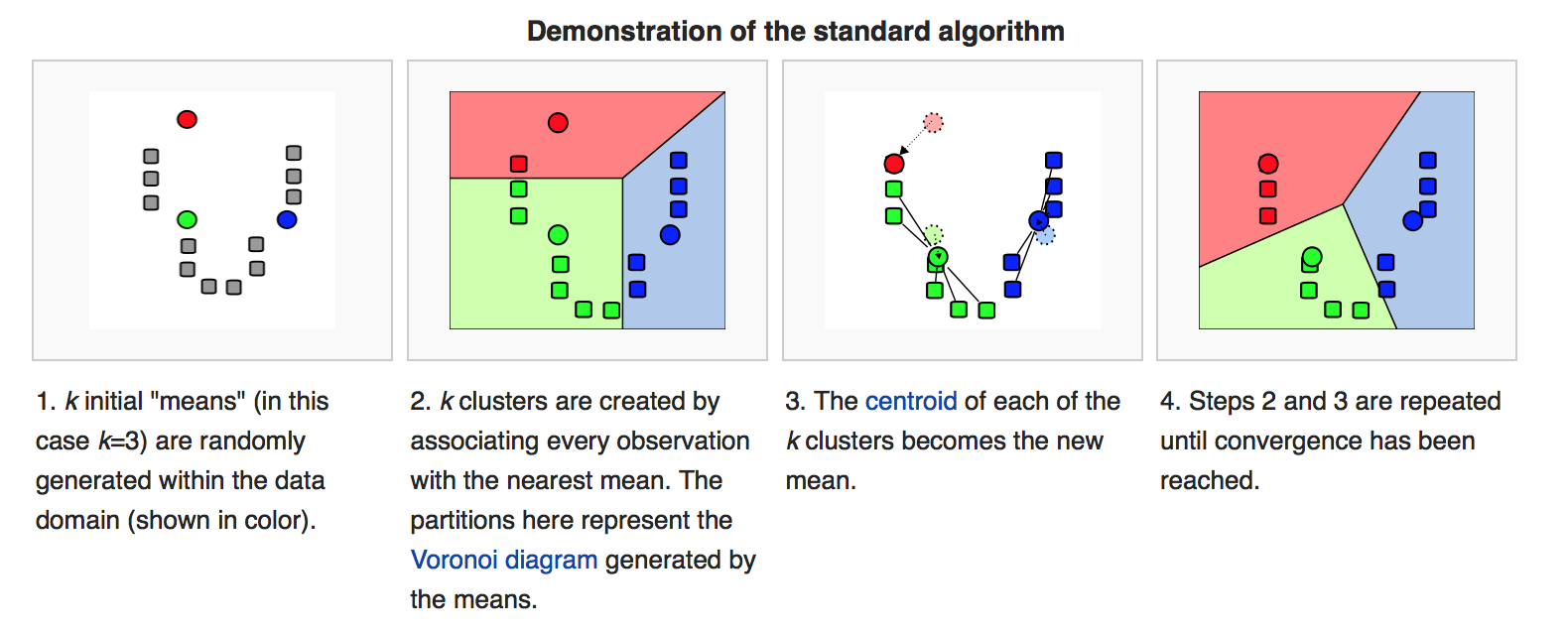
*출처 : https://brilliant.org/wiki/k-means-clustering/

1. 초기점(k) 설정

• k는 중심점(centroid)이자, 묶일 그룹(cluster)의 수와 같다.
• 위 예시에서는 k=3으로 설정(동그라미)

2. 그룹(cluster) 부여

• k개의 중심점(동그라미)과 개별 데이터(네모)간의 거리를 측정한다.
• 가장 가까운 중심점으로 데이터를 부여한다.

3. 중심점(centroid) 업데이트

• 할당된 데이터들의 평균값(mean)으로 새로운 중심점(centroid)을 업데이트한다.

4. 최적화

• 2,3번 작업을 반복적으로 수행한다.
• 변화가 없으면 작업을 중단한다.

결국 아래와 같은 목적함수를 최소화하는 것을 목표로 하는 알고리즘인 것이다.

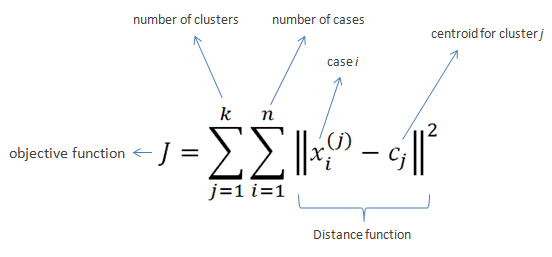
*출처 : https://www.saedsayad.com/clustering_kmeans.htm

중심점 업데이트(3번)를 위해 평균값을 사용하기 때문에 K-means라고 불리며, 이상치에 영향을 받는 단점을 보완하기 위해 중간값을 활용한 K-medoids방법도 있다.

Python의 Scikit learn 라이브러리에서 제공하는 KMeans함수로 이를 간단하게 구현할 수 있다.

KMeans(n_cluster=, init=, random_state=)

함수의 파라미터는 위 3가지 정도만 알아두면 될 것 같다.

• n_cluster : k의 수
• init : 초기값 지정(default는 random)(배열의 수는 k와 동일해야함)
• random_state : random 시드 설정

K-means는 초기값에 따라 군집이 다르게 형성되므로 매번 다른 결과가 나오는 것을 방지하기 위해, 직접 초기값을 지정하거나(init) 시드를 고정(random_state)하는 방법이 있다.

예제 데이터는 Iris 데이터를 사용하였다

from sklearn import datasets
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

iris = datasets.load_iris()
df = pd.DataFrame(iris.data)
df.columns=['Sepal length','Sepal width','Petal length','Petal width']
df = df[['Sepal length','Sepal width']].copy() 

df.head()

	Sepal length	Sepal width
0	5.1	3.5
1	4.9	3.0
2	4.7	3.2
3	4.6	3.1
4	5.0	3.6

초기값 3개를 직접 지정하였고 가시적으로 확인하기 위하여 2개 변수만 사용하려고 한다.

x1,y1 = 5, 3.5
x2,y2 = 6, 3
x3,y3 = 7.5, 4

plt.figure(figsize=(7,5))
plt.title("Before", fontsize=15)
plt.plot(df["Sepal length"], df["Sepal width"], "o", label="Data")
plt.plot([x1,x2,x3], [y1,y2,y3], "rD", markersize=12, label='init_Centroid')
plt.xlabel("Sepal length", fontsize=12)
plt.ylabel("Sepal width", fontsize=12)
plt.legend()
plt.grid()
plt.show()

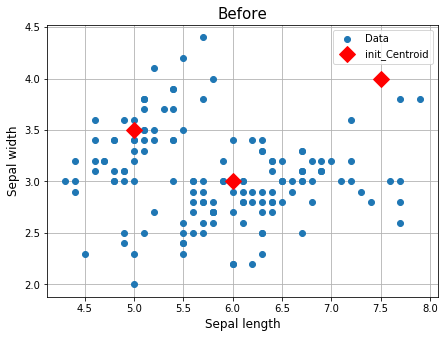
이제 KMeans함수로 학습을 한 후에, 결과를 추출해보자.

• labels_ : 최종적으로 군집화된 라벨을 추출
• cluster_centers_ : 최종 중심점(centroid) 배열을 추출

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, init=np.array([(x1,y1),(x2,y2),(x3,y3)])).fit(df)
df['cluster'] = kmeans.labels_
final_centroid = kmeans.cluster_centers_

plt.figure(figsize=(7,5))
plt.title("After", fontsize=15)
plt.scatter(df['Sepal length'],df['Sepal width'],c=df['cluster'])
plt.plot(final_centroid[:,0], final_centroid[:,1], "rD", markersize=12, label='final_Centroid')
plt.xlabel("Sepal length", fontsize=12)
plt.ylabel("Sepal width", fontsize=12)
plt.legend()
plt.grid()
plt.show()

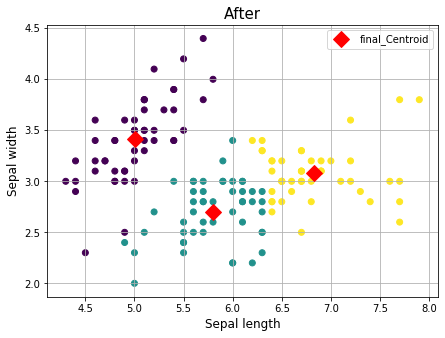
중심값(Centroid)이 이동하였고, 이것을 기반으로 군집화된 결과를 확인할 수 있다.

DBSCAN

DBSCAN는 밀도기반(Density-based) 클러스터링 방법으로 “유사한 데이터는 서로 근접하게 분포할 것이다”는 가정을 기반으로 한다. K-means와 달리 처음에 그룹의 수(k)를 설정하지 않고 자동적으로 최적의 그룹 수를 찾아나간다.

아래 그림을 통해 그 원리를 알아보자.

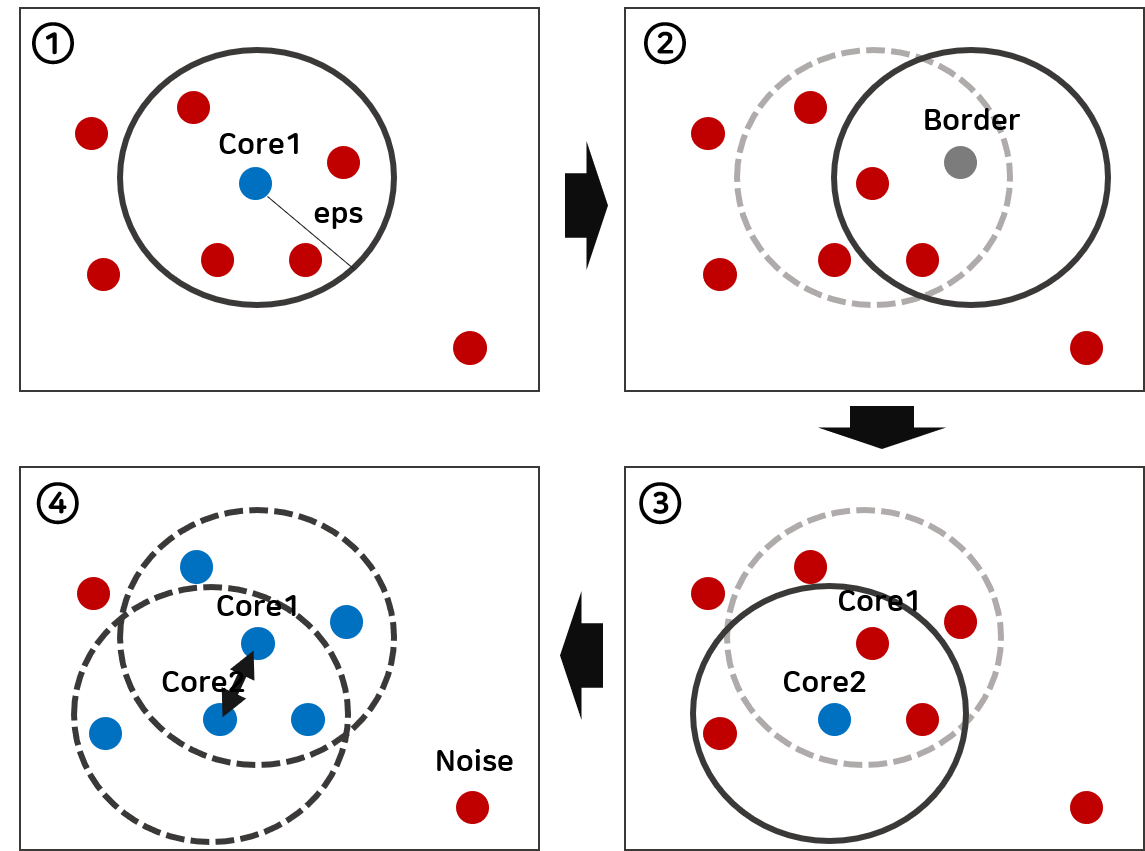
1. 먼저 하나의 점(파란색)을 중심으로 반경(eps) 내에 최소 점이 4개(minPts=4)이상 있으면, 하나의 군집으로 판단하며 해당 점(파란색)은 Core가 된다.
2. 반경 내에 점이 3개 뿐이므로 Core가 되진 않지만 Core1의 군집에 포함된 점으로, 이는 Border가 된다.
3. 1번과 마찬가지로 Core가 된다.
4. 그런데 반경내의 점중에 Core1이 포함되어 있어 군집을 연결하여 하나의 군집으로 묶인다.

이와 같은 방식으로 군집의 확산을 반복하면서, 자동으로 최적의 군집수가 도출된다.

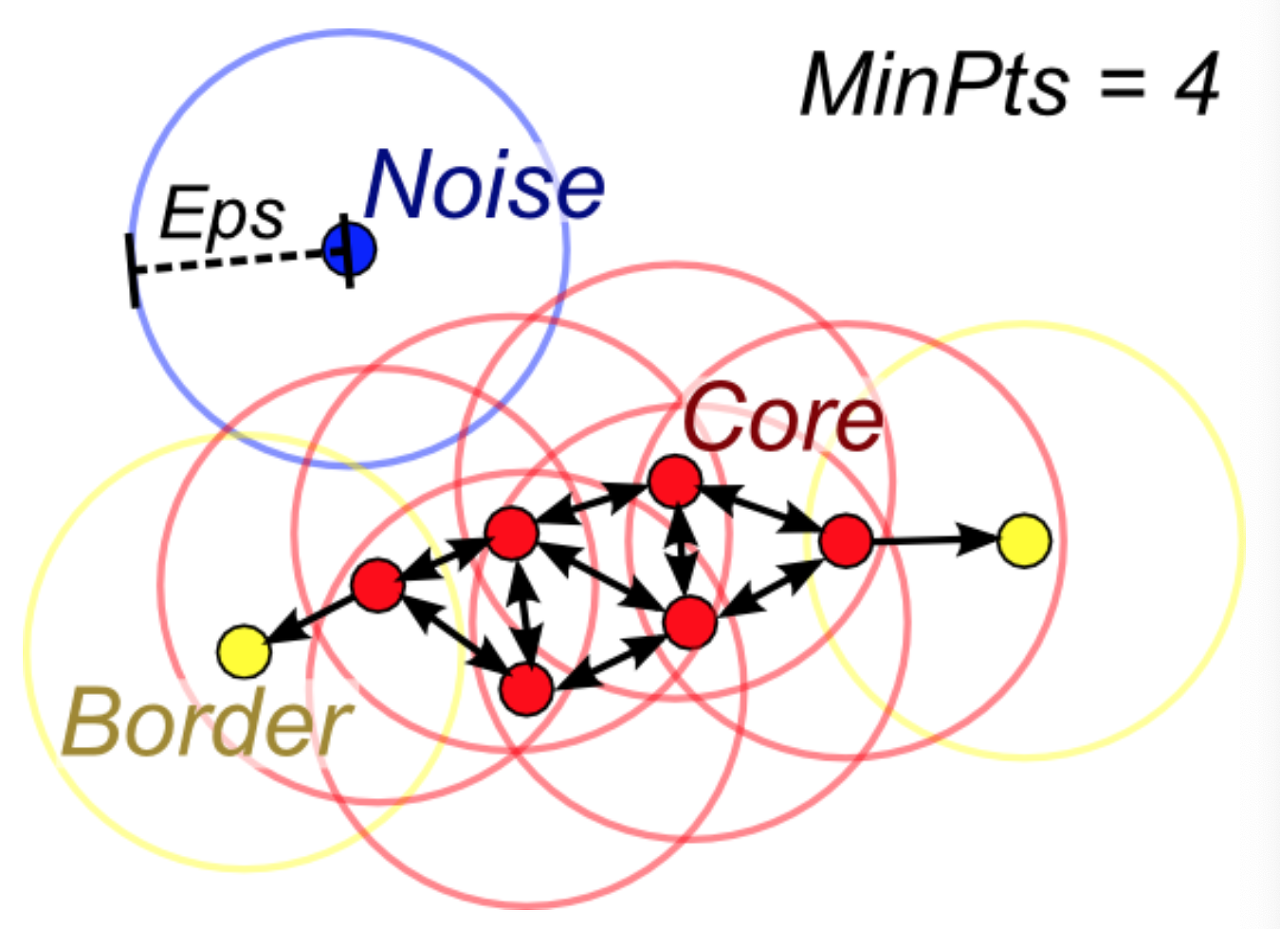
용어를 정리해보면 다음과 같다.

• minPts : 반경 내 최소 개체(point) 수
• eps(epsilon) : 군집화할 반경
• Core : 중심점(minPts를 만족할 경우)
• Border : 경계점(minPts를 만족하진 않지만, 어느 Core 반경에 속한 경우)
• Noise : 어느 군집에도 속하지 않는 점

Python으로 이제 구현해보자.

밀도기반 군집화의 명확한 이해를 위해, 예제 데이터로 Moon 데이터셋을 활용하였다.
Moon 데이터는 make_moons함수로 생성할 수 있으며 샘플 수(n_samples)와 분산정도(noise)를 조절해서 생성할 수 있다.

Scikit learn 라이브러리에서 제공하는 DBSCAN함수로 이를 간단하게 구현할 수 있다.
DBSCAN(eps=, min_samples=)

• eps : 반경 설정(속성값의 단위)
• min_samples : 최소 개체 수

함수의 파라미터는 위 2가지 정도만 알아두면 될 것 같다.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons

x,y = make_moons(n_samples=300, noise=0.05, random_state=42)
df=pd.DataFrame(x)
df.head()

	0	1
0	0.622519	-0.372101
1	1.904269	-0.136303
2	-0.069431	0.456117
3	0.933899	0.237483
4	1.180360	-0.490847

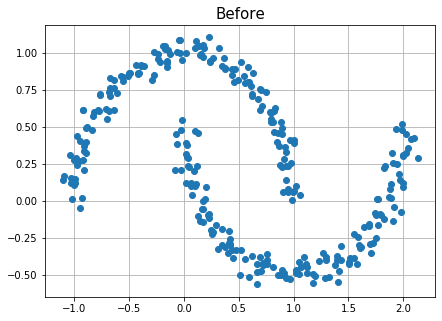
산점도를 뿌려보면 다음과 같다.

plt.figure(figsize=(7,5))
plt.title("Before", fontsize=15)
plt.plot(df[0], df[1], "o")
plt.grid()
plt.show()

이제 DBSCAN함수로 클러스터링을 수행해보자.

from sklearn.cluster import DBSCAN
db_scan = DBSCAN(eps=0.3, min_samples=5).fit(df.values)
df['cluster_db'] = db_scan.labels_

plt.figure(figsize=(7,5))
plt.title("After - DBSCAN", fontsize=15)
plt.scatter(df[0],df[1],c=df['cluster_db'])
plt.grid()
plt.show()

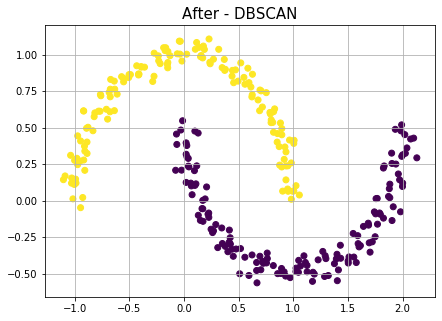
이와 같이 Moon 데이터셋은 밀도 기반(Density-based)의 특징을 잘 보여줄 수 있는 예제이다.

그럼 동일 데이터로 K-means를 수행하면 어떨까?

K-means와 DBSCAN 비교

위와 동일한 Moon 데이터셋으로 KMeans를 활용해 작업을 수행해본 결과이다.

from sklearn.cluster import KMeans
kmeans_ = KMeans(n_clusters=2, random_state=42).fit(df.values)
df['cluster_km'] = kmeans_.labels_

plt.figure(figsize=(7,5))
plt.title("After - KMeans", fontsize=15)
plt.scatter(df[0],df[1],c=df['cluster_km'])
plt.grid()
plt.show()

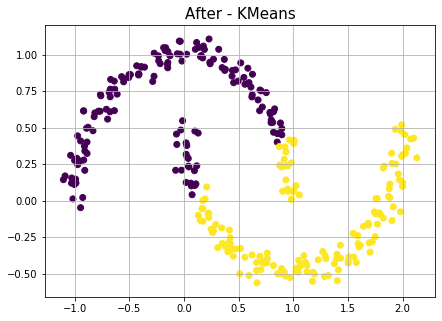
앞서 배웠던 내용처럼 K-means 군집분석 방법은 중심점(Centroid)라는 개념이 있으며, 이 중심점은 평균값(mean)에 의해 갱신되는 특징을 가지고 있기 때문이다.

이렇게 기하학적인 특징을 가진 데이터나 이상치가 있는 경우 K-means 왜곡된 결과를 초래할 가능성이 있으므로 EDA(탐색적 자료분석)를 통해 적절한 방법론을 적용할 줄 알아야 한다.

K-means

• 군집의 수(k)를 미리 결정
• 중심점(Centroid) 갱신을 통해 비용함수를 최적화
• 이상치에 영향을 많이 받음

DBSCAN

• 반경(eps), 최소 개체 수(minPts)를 미리 결정
• 자동적으로 군집의 수 결정
• 군집 간 개체들이 섞이지 않음(최소 반경 내에 한해서)
• 노이즈 개념으로 이상치 검출이 가능

Reference

https://brilliant.org/wiki/k-means-clustering/

https://bcho.tistory.com/1203

https://bcho.tistory.com/1205

https://todayisbetterthanyesterday.tistory.com/62

https://m.blog.naver.com/PostView.nhn?blogId=samsjang&logNo=221023672149&proxyReferer=https:%2F%2Fwww.google.com%2F