Yonggeun Shin

Yonggeun Shin

시행착오가 밑거름이 되는 공간

[Algorithm] 다이나믹 프로그래밍 (Dynamic Programming)

업데이트:

개요

jpg

이번 포스팅은 최적해를 계산할 때 연산속도를 개선하고 메모리 공간을 효율적으로 사용할 수 있는 다이나믹 프로그래밍(dynamic programming)에 대해 알아보자. 알고리즘이라기 보다는 계산 효율성을 향상시키기 위한 수단으로 이해할 수 있다.


다이나믹 프로그래밍

다이나믹 프로그래밍 (또는 동적계획법)은 문제 해결을 위한 연산 중 반복적인 연산에 대해서 한 번만 연산을 해서 저장해두고 이후 동일한 연산에 대해서는 저장된 값을 가져와 사용하자는 것이 기본 아이디어이다. 즉, 중복되는 연산을 줄임으로써 연산량이 감소하는 것이다.

모든 문제에 적용될 수는 없으며, 다음 조건을 만족할 때 사용한다.

  1. 큰 문제를 작은 문제로 나눌 수 있다.
  2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.

또한 문제를 해결하는 방식에 따라 두 종류로 구분된다.

  1. 탑다운(Top-Down) 방식 : 큰 문제를 해결하기 위해 작은 문제를 호출
    • 재귀함수로 구현
    • Memoization 방식
  2. 바텀업(Bottom-Up) 방식 : 작은 문제부터 차근차근 답을 도출
    • 반복문으로 구현
    • Tabulation 방식


피보나치 수열에 적용

다이나믹 프로그래밍의 조건을 만족하는 대표적인 예시로 피보나치 수열이 있다.

이는 첫째항과 둘째항은 1이고, 셋째항부터는 앞의 두 항을 더한 값으로 이어진다.

이를 점화식으로 표현하면 다음과 같다.

\[a_n=a_{n-1}+a_{n-2}, a_1=a_2=1\]

이를 이전 포스팅에서는 재귀함수로 간단하게 구현했지만, 시간복잡도는 $O(2^N)$로, N이 커짐에 따라 기하급수적으로 연산량이 증가해 현실적으로 계산할 수가 없게 된다.

아래 그림은 $a_6$을 구하기 위한 하위 원소들을 그래프 형태로 나타낸 것이다.

png

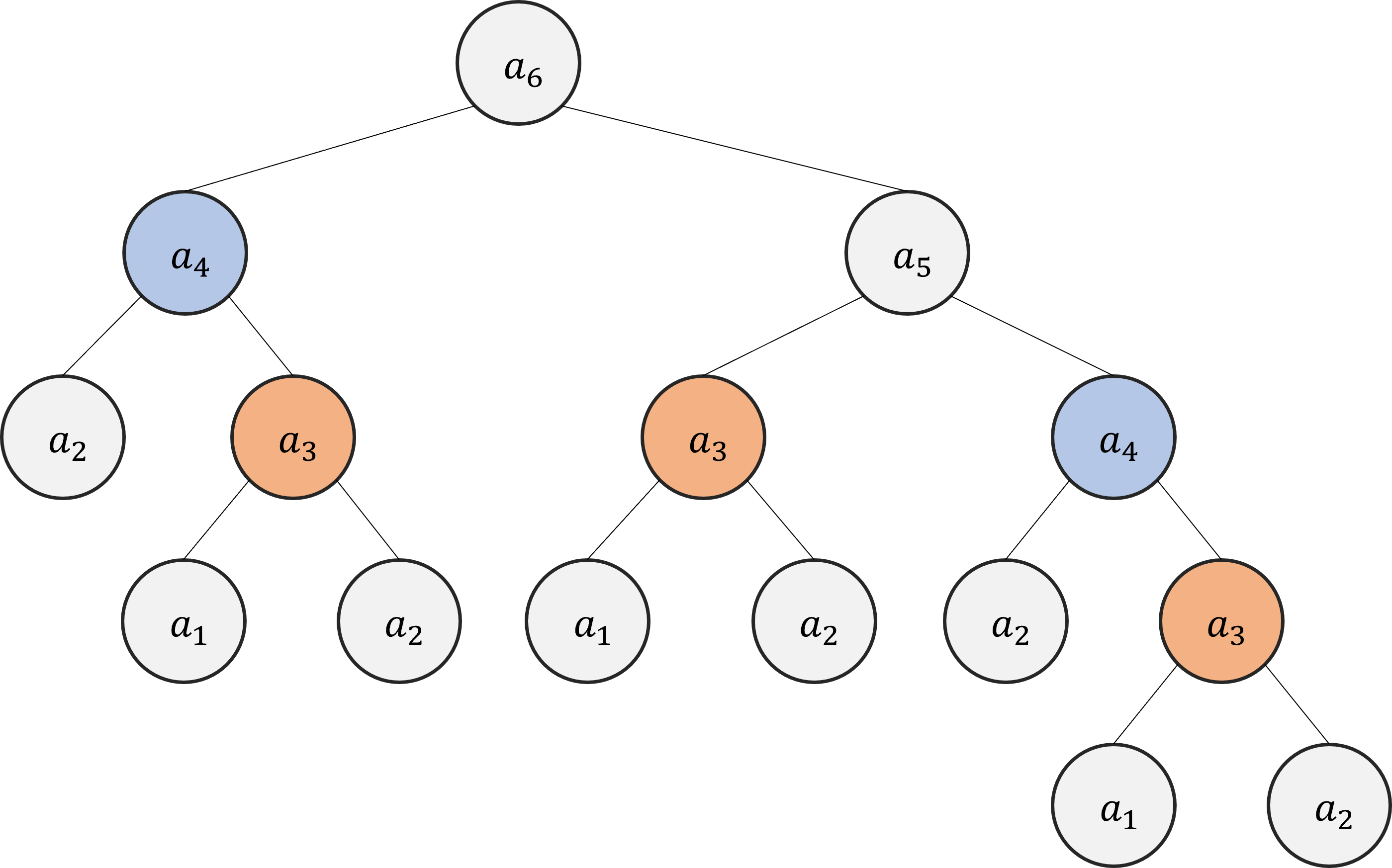
즉, 피보나치 수열은 하나의 항을 구하기 위해서는(큰 문제) 하위 항들(작은 문제)을 연쇄적으로 계산해야한다.

그런데 같은 색으로 표시된 $a_4$와 $a_3$은 각각 2번, 3번씩 반복 사용된다. 이렇게 반복되는 작은 하위 문제들의 연산은 미리 저장해두었다가 사용하면 연산량을 줄일 수 있다.

탑다운 방식

위 아이디어를 탑다운 방식으로 구현한 코드이다.

d=[0]*100 # Memoization을 위한 저장공간
def fibo_dp(n):
    if n<=2:
        return 1
    if d[n]!=0:
        return d[n]
    print("f("+str(n)+")", end=' ')
    d[n]=fibo_dp(n-1)+fibo_dp(n-2)
    return d[n]

fibo_dp(6)

f(6) f(5) f(4) f(3)

기존 피보나치 수열 구현코드와 약간의 차이가 있다.
d라는 DP table를 항의 개수만큼 만들고, 새로 계산할 항은 저장해두고 이미 계산된 항은 가져와서 사용하는 방식이다.
즉, 결과를 보면 f(6)의 계산을 위해 쭉 재귀를 타고 내려가다가 f(1)과 f(2)을 가져와서 f(3)을 푸는데 사용하고 f(4)를 푸는데 f(3)을 사용하는 식으로 진행된다.

즉, 한번 계산한 값은 다시 계산하지 않고 가져와서 사용한다.

따라서 위 출력결과 처럼 시간 복잡도는 $O(N)$ 이다.

바텀업 방식

바텀업 방식은 제일 작은 문제부터 차근차근 dp 테이블에 저장하여 큰 문제에 도달하는 방식으로, 반복문으로 구현한다.

저장되는 순서로 보면 탑다운이나 바텀업이나 하위 문제부터 저장되어 상위문제를 계산할때 가져와 사용하는 것은 동일하다.

그러나 재귀함수의 호출 순서가 큰 문제에서 하위 문제로 내려가며, 반복문은 작은 문제부터 올라가므로 아이디어 접근 방식의 차이가 있다는 것이다.

d=[0]*100
d[1]=1
d[2]=1
n=99

for i in range(3,n+1):
    d[i]=d[i-1]+d[i-2]
print(d[n])

일반적으로 바텀업 방식이 많이 사용된다.


유용한 팁

사실 개념을 배워도 어느 정도 익숙해지지 않으면 실제 문제에 바로 다이나믹 프로그래밍을 활용하기가 어렵다. 아래의 순서로 문제를 파악하고 구현하는 습관을 들이도록 하자.

1. 다이나믹 프로그래밍으로 풀 수 있는 문제인지 확인

  • 위 2가지 조건을 충족하는지 확인

2. 결정변수 정의

  • 찾아야 하는 해(피보나치에서는 $a_n$)를 정의

3. 점화식(중요)

  • DP는 점화식만 잘 정의하면 이미 풀었다고 할 수 있을 정도로 중요
  • 큰 문제와 하위 문제들간의 관계를 잘 파악해서 점화식 세워보기

3. DP 테이블에 저장하기

  • 점화식에서 반복 연산이 언제 어떻게 발생하는지 확인
  • 저장하고 꺼내쓰는 메커니즘

4. 가장 하위 문제의 파악

  • 가장 하위 문제는 피보나치 수열처럼 직접 값을 미리 넣어주거나, 종료조건을 만들어 주어야함

5. 구현

  • 탑다운(재귀) 또는 바텀업(반복문) 사용


Reference

이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈

https://hongjw1938.tistory.com/47

댓글남기기

참고