[Algorithm] 탐욕 알고리즘 (Greedy algorithm)

개요

이번 포스팅은 그리디(Greedy) 또는 탐욕 알고리즘에 대한 글이다. 가장 기초가 되는 알고리즘이기도 하며 복잡한 문제를 단순하고 강력하게 해결할 수 있는 장점이 있다.

그리디 알고리즘이란?

탐욕법이라고도 하는 그리디(Greedy) 알고리즘은 “현재 상황에서 최적이라고 생각하는 해를 선택“하는 방법이다.
그러나 말그대로 앞으로 남은 선택들을 고려하지 않고 현재 상황만 고려하기 때문에 항상 최적해(Global optimum)를 보장하지는 않는다.

예를 들어, 아래 그림과 같은 트리구조의 경로가 있고 우리는 경로마다 놓여있는 돈을 얻을 수 있다고 해보자.

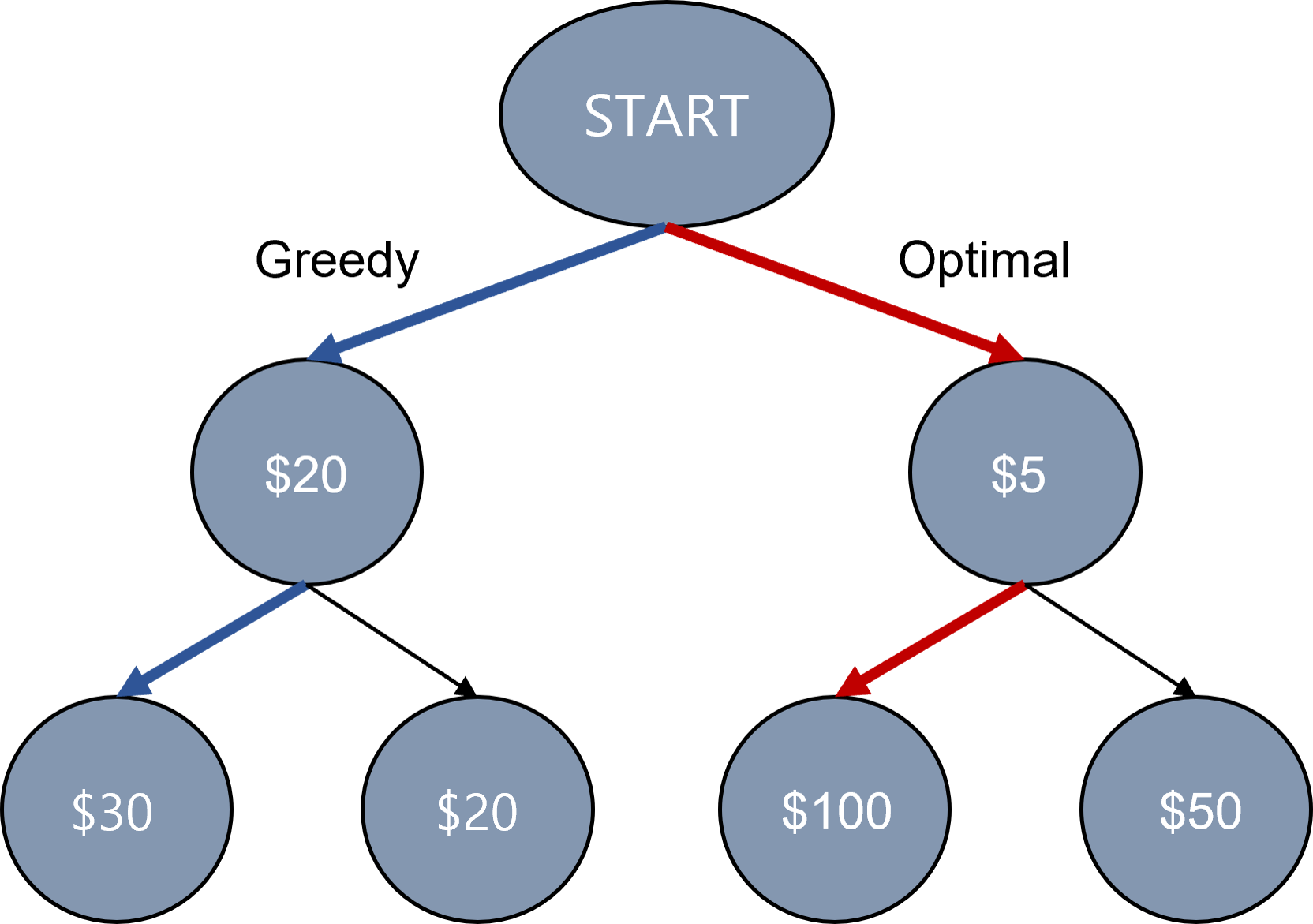
제일 많은 돈을 얻기 위해서는 빨간색 경로로 이동해야 하지만, 눈 앞에 놓인 갈림길에서 높은 금액만을 선택하는 그리디 방법은 파란색 경로로 이동한다. 따라서 $50 밖에 얻지 못한다.

그리디 알고리즘의 정당성

그리디 알고리즘으로 최적해를 도출하기 위해서는 아래 두가지 조건을 만족해야 한다.

1.탐욕적 선택 속성 (greedy choice property)
탐욕적인 선택이 항상 안전하다는 것이 보장된다는 의미이다. 즉, 그리디한 선택이 언제나 최적해를 보장해야한다.

2. 최적 부분 구조 (optimal substructure)
부분 최적해(Local optimum)들이 모여 전체 최적해(Global optimum)를 구할 수 있는 경우이다. 즉, 전체 문제가 여러 부분 문제로 분할되며, 이 단계 하나하나에 대한 최적해가 도출되어야 한다는 의미이다.

예를 들면, 아래와 같은 경로 찾기가 있을 수 있다.

위 그림 처럼 도시간 이동을 위와 같이 밖에 할 수 없다고 했을 때, 서울에서 대전의 최단경로(Local optimum)와 대전에서 부산의 최단 경로(Local optimum)가 모여 서울에서 부산까지 가는 최단 경로(Global optimum)가 될 것 이다.

예제 : 거스름돈 문제

대표적인 문제는 거스름돈 문제가 있다.

당신은 음식점의 계산을 도와주는 점원이다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러 줘야할 동전의 최소 개수를 구하라. (단, N은 항상 10의 배수)

풀이 및 코드

# solve
N=1260
cnt=0
for i in [500,100,50,10]:
    num_ = N//i
    N=N-num_*i
    cnt+=num_
print(cnt)

# reference
N=1260
cnt=0
for i in [500,100,50,10]:
    cnt += N//i
    N%=i
print(cnt)    

아이디어는 두가지이다.

• 최소 동전의 개수이므로 큰 동전(500원)부터 거슬러준다.
• 거슬러 준 만큼 N에서 뺀다.

*몫의 계산으로 동일하게 접근했지만, 단순히 N에서 빼는 것이 아니라 나머지를 계산해주면 더 간단해진다.

논의

위 문제가 그리디하게 풀리는 이유는 가지고 있는 동전의 단위가 모두 배수의 형태이기 때문이다. 따라서 작은 단위의 동전을 종합해 다른 해가 나올 수 없으므로 언제나 최적해를 보장한다.

하지만 거스름돈 문제에서 단위가 서로 배수의 형태가 아니라, 무작위로 주어지는 경우에는 그리디가 아닌 다이나믹 프로그래밍으로 해결해야한다.

Reference

이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈
https://loosie.tistory.com/515